 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| перколяционного процесса в наноматериалах
КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ ПЕРКОЛЯЦИОННОГО ПРОЦЕССА В НАНОМАТЕРИАЛАХ
Методические указания к выполнению лабораторной работы № 2 по дисциплине «Компьютерное моделирование процессов нанотехнологий»
Курск 2012 г.
УДК 51-72, 519.8, 530.1
Составители: А.М.Стороженко, И.А.Шабанова
Рецензент Директор РИЦ, д.ф.-м.н., профессор А.П. Кузьменко
Компьютерное моделирование перколяционного процесса в наноматериалах: методические указания к лабораторной работе № 2 по дисциплине «Компьютерное моделирование процессов нанотехнологий» / Юго-Зап. гос. ун-т; сост.: А.М.Стороженко, И.А.Шабанова. Курск, 2012. 10 с.: ил. 3. Библиогр.: 4 назв.
Излагаются методические рекомендации по выполнению лабораторной работы №2, в которой рассматриваются основные принципы моделирования перколяционных процессов в наноматериалах. Содержатся краткое описание алгоритмов стохастического моделирования пористой среды и построения перколяционного кластера, задания и вопросы для контроля знаний. Методические указания соответствуют требованиям Государственного образовательного стандарта высшего профессионального образования и рабочего учебного плана направления подготовки 210600.62 Нанотехнология, степень (квалификация) – бакалавр техники и технологии. Предназначены для студентов дневной формы обучения.
Текст печатается в авторской редакции
Подписано в печать . Формат 60 x 84 1/16. Усл. печ. л. 0,58. Уч.-изд. л. 0,53. Тираж экз. Заказ . Бесплатно. Юго-Западный государственный университет. 305040 Курск, ул. 50 лет Октября, 94.
Лабораторная работа № 2
Компьютерное моделирование перколяционного процесса в наноматериалах
Цель работы: освоить методику моделирования процесса перколяции в пористом материале на основе стохастической модели.
Программное обеспечение: среда Delphi–7 или C++ Builder.
ЗАДАНИЕ ПО РАБОТЕ
1. По предложенным алгоритмам составить программу оккупации соседей и определения порога перколяции (протекания среды) в среде Borland Delphi–7 или C++ Builder. 2. Реализовать в среде Delphi–7 или C++ Builder алгоритм визуализации процесса перколяции. 3. Составить отчет по работе, содержащий - задание и цель лабораторной работы, - описание входных и выходных данных, - принтскрин разработанной формы, - перечисление используемых промежуточных переменных и компонентов формы, - описание разработанных классов и/или процедур (функций), - блок-схемы подпрограмм, - результаты тестирования программы, - листинг рабочего проекта.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ РАБОТЫ
Эволюция представлений капиллярно-пористых структур на регулярной исходной решетке привела к идеям применения современных алгоритмических методов для моделирования стохастических систем капилляров с заданными свойствами, получившим распространение в задачах перколяции или протекания. В наиболее общей постановке в задачах перколяции рассматривается динамика распространения фронта одной жидкости в пористой среде, насыщенной другой жидкостью или газом. Таким образом, в задачах перколяции рассматривается начальная фаза процесса фильтрации жидкостей и/или газов в пористой среде. Характерной особенностью процесса перколяции является чрезвычайно неустойчивый характер, оказывающий существенное влияние на дальнейшее развитие всего процесса фильтрации. Простейший вариант синтеза капиллярной перколяционной модели состоит из следующих этапов. Алгоритм 1 1. Определяется геометрия моделируемой области, ее макроскопические характеристики и граничные условия. Затем в области формируется регулярная (как правило, прямоугольная) решетка узлов. 2. Выбирается начальное приближение значения геометрической пористости и формируется множество узлов, содержащих поры. 3. Начинается процесс инжекции жидкости в соответствии с установленными граничными условиями. Заметим, что распространение жидкости возможно только по узлам решетки, непосредственно связанным с источником. По завершении роста перколяционных кластеров полученная структура фиксируется в качестве капиллярной модели пористой среды. 4. С учетом связности определяются характеристики полученной структуры. Рассмотрим основные эмпирические характеристики пористой среды. Одним из важнейших показателей является объемная пористость:
где VP –полный объем порового пространства, VM – объем структурной матрицы, VO – общая величина элементарного репрезентативного объема пористой среды. При определении пористости следуем различать полную ПVO и эффективную ПVS пористость. Понятие эффективной пористости базируется на представлении о связности некоторой части пор между собой. В результате в поровом пространстве формируется единая система пор, связанная с поверхностью пористого тела и проницаемая для внешней среды. Различие между полной и эффективной пористостью можно охарактеризовать коэффициентом объемной связности
принимающим значения от kVS = 0 при полностью изолированной до kVS = 1 при полностью открытой структуре порового пространства. Примеры капиллярный пористых структур, построенные с помощью вышеописанной перколяционной модели на регулярной квадратной решетке размером 22×20 узлов при начальных значениях геометрической пористости 0,475; 0,575 и 0,675 приведены на рис. 1.
а) б) в) Рис. 1. Стохастические модели пористой среды. Перколяционная система капилляров на регулярной решетке: а) геометрическая пористость ПVO = 0,477, эффективная пористость ПVS = 0,177; б) ПVO = 0,561, ПVS = 0,389; в) ПVO = 0,666, ПVS = 0,627 Как следует из определения, эффективная пористость решетки в перколяционных моделях не превышает геометрической и стремится к последней по мере роста ее значений. Очевидно, что коэффициент связности перколяционных моделей также не превышает единицы и в показанных случаях равен 0,371; 0,693 и 0,941. Протекание на большей части граничных узлов наступает при значении геометрической пористости выше так называемого «порога протекания» Пg = 0,59275±0,0003, что вполне согласуется с представленными результатами моделирования. Отметим, что при выборе других начальных условий общий вид и эффективные характеристики перколяционных кластеров могут отличаться от приведенных выше. Одной из первоначальных задач, возникающих при моделировании перколяционного процесса, является задача выделения подмножества узлов, непрерывным образом связанных с заданным узлом (или некоторой их совокупностью). Вопрос об оценке вероятности возникновения пути, связывающего две противоположные стороны ограниченной четырехсвязной решетки, является частным случаем этой задачи. Среди множества алгоритмов для решения поставленной задачи наибольшей эффективностью по мнению ряда авторов отличается алгоритм, предложенный в различные годы П.Лисом, Дж.Хаммерсли и З.Александровицем. Основная идея алгоритма состоит в следующем. Среди свободных достижимых узлов формируется некоторое начальное множество. Для каждого из начальных узлов строится множество соседних (периметр множества) и те из узлов, которые являются достижимыми и не принадлежат к какому-либо другому множеству, присоединяются к начальному. Затем выполняется построение периметра для нового «начального множества» и процесс повторяется до исчерпания свободных узлов или достижения какой-либо заданной точки. Таким образом, построение перколяционного кластера из произвольной точки квадратной четырехсвязной решетки может быть осуществлено следующим образом. Алгоритм 2 1. Все недостижимые узлы перколяционной решетки помечаются цифровой меткой «0» и исключаются из дальнейшего рассмотрения. 2. Все потенциально достижимые узлы помечаются меткой «1». 3. Все узлы, принадлежащие формируемому кластеру, помечаются меткой «2». 4. Далее, формируется периметр множества «2» и все «1» из этого периметра помечаются меткой «3». 5. По завершении проверки все «3» присоединяются к формируемому кластеру, то есть подвергаются повторной маркировке цифровой меткой «2». Примеры построения перколяционных кластеров на четырехсвязной решетке размером 50×50 при различной доле достижимых узлов р показаны на рис. 2. Черным цветом обозначены достижимые узлы, принадлежащие перколяционному кластеру; светло-серым цветом – достижимые узлы, оставшиеся незанятыми, а белым цветом – недостижимые узлы.
а) б) Рис. 2. Перколяционные кластеры на четырехсвязной решетке размером 50×50: а) р = 0,595; б) р = 0,605 Вообще говоря, использование цифровых меток не является обязательным, но алгоритм, реализованный с их применением, получается менее требовательным к объему оперативной памяти. У ряда авторов встречаются предложения о более радикальном способе экономии памяти, предусматривающем отказ от единовременной генерации и хранения крупного массива псевдослучайных чисел. Идея основана на том факте, что при фиксации начального элемента современные алгоритмы всегда генерируют одну и ту же последовательность псевдослучайных чисел. Исходя из этого, предлагается при проверке очередного элемента массива сохранять лишь его индекс и генерировать всю псевдослучайную последовательность от начала до текущей точки заново. Заметим, однако, что необходимость в сохранении индексов элементов формируемого кластера все же остается, следовательно, существенный выигрыш этот подход сможет принести лишь при достаточно «разреженной» структуре перколяционного кластера. Хорошим примером перколяции служит явление электрического пробоя в двумерной квадратной решетке, состоящей из узлов, которые могут быть проводящими или непроводящими. В начальный момент времени все узлы сетки являются непроводящими. Постепенно под влиянием внешнего источника число проводящих узлов увеличивается за счет уменьшения непроводящих узлов сетки. При этом узлы замещаются случайным образом, то есть выбор любого из узлов для замещения является равновероятным для всей поверхности решетки. Рост проводящих узлов в момент достижения порога перколяции обеспечит протекание тока через решетку по пути, образованному непрерывной цепочкой проводящих узлов, что и приведет далее к пробою (рис. 3).
Рис. 3. Иллюстрация явления перколяции с порогом 6/16 Среди методов моделирования перколяционных кластеров наиболее распространенным является метод Монте–Карло. Моделирование перколяционного процесса оккупации средой дискретной прямоугольной решетки выполняется с применением генератора случайных чисел. Сущность алгоритма перколяции состоит в следующем. Алгоритм 3. Оккупация ячеек средой. – задать фиксированное число р в интервале от 0 до 1 (вероятность оккупации ячейки средой); – последовательно, для каждой i-й ячейки прямоугольной решетки, сгенерировать случайное число а в интервале от 0 до 1, которое сравнить с р; – если а < р , то i-й ячейке решетки присвоить статус «оккупирована средой» (в приводимом далее примере ячейка просто закрашивается в черный цвет), в противном случае ячейка оставляется свободной (не закрашивается). Если вероятность р мала, то можно ожидать, что среда оккупирует лишь малые изолированные участки решетки (кластеры). В противном случае, то есть когда р ≈ 1, – большинство оккупированных средой ячеек образуют один большой кластер, который протянется от одной стороны решетки до другой. Говорят что такой соединяющий кластер «перекидывается» через решетку. При таком подходе к моделированию перколяционного процесса порог перколяции, о котором речь выше, может быть определен экспериментально по следующему алгоритму. Алгоритм 4. Вычисление порога перколяции – организовать внешний цикл дискретного увеличения р с шагом Δ; – выполнить все шаги Алгоритма 1 для каждого рi = Δ·i : на некотором k–м шаге величина вероятности рk достигнет «порогового» значения, при котором: для р ≥ рk существует один соединяющий кластер, или путь; для р < рk нет ни одного соединяющего кластера; – вывести на печать в качестве результатов номер шага достижения порога перколяции (k) и собственно найденную величину порога рk. Величину рk и называют порогом перколяции. Качественное изменение свойств среды при достижении некоторым непрерывно изменяемым параметром среды (р) конкретного значения (порога перколяции рk), переводя ее из состояния, не содержащего соединяющий кластер, в состояние с одним соединяющим кластером в литературе называется фазовым переходом.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Изложите сущность алгоритма оккупации ячеек стохастической модели средой. 2. Изложите суть алгоритма вычисления порога перколяции. 3. Что называется порогом перколяции? 4. Приведите примеры процессов перколяции. 5. Поясните принцип работы программы, приведенной в настоящей работе.
ОСНОВНЫЕ ИСТОЧНИКИ 1. Ибрагимов И.М. Основы компьютерного моделирования наносистем. Учебное пособие / И.М. Ибрагимов, А.Н. Ковшов, Ю.Ф. Назаров. - М. : Лань, 2010. - 384 с. : ил. - (Учебники для вузов. Специальная литература). - ISBN 978-5-8114-1032-3 : 379р. 70к. 2. Архангельский А.Я. Программирование в Delphi 7. М.: ООО «Бином-Пресс», 2003 г. — 1152 с.
ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА
1. Москалев П.В., Шитов В.В. Математическое моделирование пористых структур. - М.: Физматлит, 2007. – 120 с. ISBN 978-5-9221-0818-8. 2. Гулд Х., Тобочник Я. Компьютерное моделирование в физике. – В 2 т.– 1992 (http://www.twirpx.com)
|



 (1)
(1)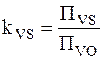 , (2)
, (2)




