Задания для аудиторной работы
Классы вычетов Теоретические сведения При делении целых чисел на натуральное целое 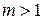 существует существует  различных остатков: различных остатков:  Соответственно этим остаткам множество Z разбивается на Соответственно этим остаткам множество Z разбивается на  непересекающихся классов сравнимых друг с другом чисел, т. е. имеющих один и тот же остаток от деления на непересекающихся классов сравнимых друг с другом чисел, т. е. имеющих один и тот же остаток от деления на  В соответствии с остатками от деления на В соответствии с остатками от деления на  эти классы будем обозначать через эти классы будем обозначать через  . Таким образом, класс . Таким образом, класс  для каждого целого для каждого целого  Любой представитель класса однозначно определяет свой класс: для каждого натурального числа Любой представитель класса однозначно определяет свой класс: для каждого натурального числа 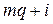 класс класс  . Поскольку остаток – по-латински residu – переводится на русский язык как вычет, то множество всех классов сравнимых друг с другом по данному модулю . Поскольку остаток – по-латински residu – переводится на русский язык как вычет, то множество всех классов сравнимых друг с другом по данному модулю  чисел называют множеством классов вычетов по модулю чисел называют множеством классов вычетов по модулю  и обозначают через и обозначают через  В силу сказанного В силу сказанного  – множество из – множество из  элементов. элементов. Заметим, что для любых классов  и для произвольных и для произвольных  суммы суммы  и и  принадлежат одному классу из принадлежат одному классу из  так как эти суммы сравнимы друг с другом по модулю так как эти суммы сравнимы друг с другом по модулю  согласно свойству 2 сравнений (см. теоретический материал к первому разделу). Аналогично, произведения согласно свойству 2 сравнений (см. теоретический материал к первому разделу). Аналогично, произведения  и и  лежат в одном классе из лежат в одном классе из  Определим операции сложения и умножения на Определим операции сложения и умножения на  Полагаем суммой Полагаем суммой  Å Å  тот единственный класс тот единственный класс  из из  в который попадают все суммы в который попадают все суммы  и и  для для  а произведением а произведением   – тот класс из – тот класс из  в который попадают произведения в который попадают произведения  для произвольных для произвольных 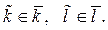 Поскольку сложение и умножение в  однозначно определяются умножением представителей классов, то свойства 1 – 5 операций сложения и умножения целых чисел (см. раздел 1) справедливы и в однозначно определяются умножением представителей классов, то свойства 1 – 5 операций сложения и умножения целых чисел (см. раздел 1) справедливы и в  1) 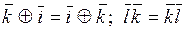 – коммутативность; – коммутативность; 2)  – ассоциативность; – ассоциативность; 3) существует нейтральный элемент:  ; ; 4) для всякого  существует единственный класс существует единственный класс  , такой, что , такой, что  , очевидно, им является класс , очевидно, им является класс  = =  ; ; 5)  – дистрибутивность. – дистрибутивность. Благодаря отмеченным свойствам операций сложения и умножения множество  в алгебре относят к классу коммутативных колец с единицей и называют кольцом классов вычетов по модулю в алгебре относят к классу коммутативных колец с единицей и называют кольцом классов вычетов по модулю  Определение 2.1. Элемент  называется обратимым, если найдется такой класс называется обратимым, если найдется такой класс  , что , что  . Тогда класс . Тогда класс  называют обратным к классу называют обратным к классу  . . Из ассоциативности умножения в кольце  вытекает, что если вытекает, что если  обратимый класс, то обратный класс определен однозначно. обратимый класс, то обратный класс определен однозначно. Лемма 2.1. Пусть  такой класс, что такой класс, что  Тогда: Тогда: 1) для каждого  произведение произведение  ; ; 2)  если если  3) отображение  инъективно и, следовательно, биективно на множестве инъективно и, следовательно, биективно на множестве  (на множестве ненулевых элементов из (на множестве ненулевых элементов из  ); ); 4)  – обратимый класс в кольце – обратимый класс в кольце  Замечание.Вусловиях леммы 2.1  поэтому, согласно критерию взаимной простоты целых чисел существуют такие целые поэтому, согласно критерию взаимной простоты целых чисел существуют такие целые  что что  Тогда Тогда  Следовательно, Следовательно,  обратный к обратный к  класс. класс. Лемма 2.2. Пусть  такой, что такой, что  . Тогда: . Тогда: 1) существует класс  , что , что  ; ; 2) существуют классы  такие, что такие, что  3) для всех  произведение произведение  то есть класс то есть класс  не обратим в кольце не обратим в кольце  Теорема 2.1. Класс  из кольца из кольца  обратим тогда и только тогда, когда обратим тогда и только тогда, когда  Если Если  простое число, то в кольце простое число, то в кольце  каждый ненулевой класс обратим. Обратный класс также обратим. Произведение обратимых классов есть обратимый класс. каждый ненулевой класс обратим. Обратный класс также обратим. Произведение обратимых классов есть обратимый класс. Поскольку  состоит из конечного множества элементов, то сложение и умножение можно задавать поэлементно в виде таблиц. состоит из конечного множества элементов, то сложение и умножение можно задавать поэлементно в виде таблиц. Пример 2.1. Напишем таблицы сложения и умножения в кольце  Из таблицы умножения непосредственно видно, что классы  и и  обратны самим себе, то есть обратимы все ненулевые классы обратны самим себе, то есть обратимы все ненулевые классы  в полном соответствии с теоремой 2.1. в полном соответствии с теоремой 2.1. Определение 2.2. Функция Эйлера – функция натурального аргумента  , которая каждому натуральному числу , которая каждому натуральному числу  ставит в соответствие ставит в соответствие
количество натуральных чисел, меньших  и взаимно простых c и взаимно простых c  . . Перечислим основные мультипликативные свойства функции Эйлера. Свойство 1.  для каждого простого числа для каждого простого числа  Свойство 2.  для каждого простого числа для каждого простого числа  и для произвольного натурального и для произвольного натурального  Свойство 3. Если  то то  . . Свойство 4. Если  – каноническое разложение числа – каноническое разложение числа  то то  . .
Пример 2.2. Вычислим  Поскольку Поскольку  то согласно свойству 4 значение то согласно свойству 4 значение  Пример 2.3. Из теоремы 2.1 следует, что в кольце  имеется в точности имеется в точности  обратимых классов. Например, обратимых классов. Например,  Значит, в кольце Значит, в кольце  имеется именно 4 обратимых элемента. Непосредственная проверка показывает, что этими классами являются имеется именно 4 обратимых элемента. Непосредственная проверка показывает, что этими классами являются  . . Теорема 2.2 (теорема Эйлера). Если для целого числа  и натурального и натурального   , то , то  Алгебраическим сравнением  -й степени с одной неизвестной называется сравнение вида -й степени с одной неизвестной называется сравнение вида  , ,
где  . . Если при подстановке в уравнение сравнения вместо  числа числа 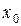 получается верное числовое сравнение, то получается верное числовое сравнение, то 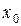 называется решением данного сравнения. При этом и любое целое число вида называется решением данного сравнения. При этом и любое целое число вида  также будет решением данного сравнения. Поэтому решением алгебраического сравнения можно считать класс вычетов также будет решением данного сравнения. Поэтому решением алгебраического сравнения можно считать класс вычетов  . Универсальным способом решения алгебраических сравнений является испытание полной системы вычетов по модулю . Универсальным способом решения алгебраических сравнений является испытание полной системы вычетов по модулю  , то есть целых чисел , то есть целых чисел  Сравнение будет иметь столько решений, сколько вычетов полной системы ему удовлетворяют. Сравнение будет иметь столько решений, сколько вычетов полной системы ему удовлетворяют. Пример 2.4. Решить сравнение  . . Решение. Среди чисел 0, 1, 2, 3, 4, 5, 6 полной системы вычетов по модулю 7 удовлетворяют данному сравнению только два числа:  . Поэтому указанное сравнение имеет два решения: . Поэтому указанное сравнение имеет два решения:  При решении сравнений часто используют преобразования, приводящие к равносильным сравнениям. Задания для аудиторной работы Задание 2.1.Вычислить  для всех натуральных для всех натуральных  от 2 до 12. от 2 до 12. Задание 2.2.Вычислить     Решение. 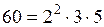 . Согласно свойству 4 функции Эйлера . Согласно свойству 4 функции Эйлера  . .
 . Поэтому согласно свойству 2 функции Эйлера . Поэтому согласно свойству 2 функции Эйлера
 . .
  не делится на все простые 2, 3, 5, 7, меньшие 10. Следовательно, 89 – число простое. Поэтому не делится на все простые 2, 3, 5, 7, меньшие 10. Следовательно, 89 – число простое. Поэтому 
Задание 2.3.В кольцах  и и  составить таблицы сложения и умножения. Найти в этих кольцах пары взаимно обратных по умножению элементов. Указать количество таких пар и сравнить это количество с составить таблицы сложения и умножения. Найти в этих кольцах пары взаимно обратных по умножению элементов. Указать количество таких пар и сравнить это количество с  и и  соответственно. соответственно. Решение аналогично решению примера 2.1. Задание 2.4.В кольце классов вычетов по модулю 15 к каждому обратимому элементу найти обратный элемент. Решениеможно получить, составив таблицу умножения в кольце  Рассмотрим ниже другой путь решения этой задачи. Рассмотрим ниже другой путь решения этой задачи. Согласно теореме 2.1 в кольце  имеется имеется  классов вычетов, взаимно простых с модулем классов вычетов, взаимно простых с модулем  Прямая проверка показывает, что эти классы составляют множество Прямая проверка показывает, что эти классы составляют множество 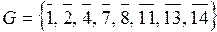 . . На языке сравнений равенство  для для  выглядит как выглядит как 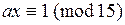 , а из теоремы Эйлера следует, что , а из теоремы Эйлера следует, что  Умножив сравнение Умножив сравнение 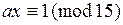 на на  , получим , получим  согласно свойствам сравнений. Последовательно вычисляем: согласно свойствам сравнений. Последовательно вычисляем:  , следовательно, , следовательно,  ; ;
 , следовательно, , следовательно,  ; ;
 ; ;
 ; ;

Задание 2.5.Найти обратные к классам  в кольце: а) в кольце: а) 
б)  Решение.  Этот наибольший общий делитель найдем по алгоритму Евклида: Этот наибольший общий делитель найдем по алгоритму Евклида:  Отсюда легко получается соотношение Безу для Отсюда легко получается соотношение Безу для   Согласно замечанию к лемме 2.1 Согласно замечанию к лемме 2.1  Проверка: Проверка: 
 Поэтому в кольце Поэтому в кольце  не существует не существует 
| 



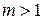 существует
существует  различных остатков:
различных остатков:  Соответственно этим остаткам множество Z разбивается на
Соответственно этим остаткам множество Z разбивается на  непересекающихся классов сравнимых друг с другом чисел, т. е. имеющих один и тот же остаток от деления на
непересекающихся классов сравнимых друг с другом чисел, т. е. имеющих один и тот же остаток от деления на  В соответствии с остатками от деления на
В соответствии с остатками от деления на  . Таким образом, класс
. Таким образом, класс  для каждого целого
для каждого целого  Любой представитель класса однозначно определяет свой класс: для каждого натурального числа
Любой представитель класса однозначно определяет свой класс: для каждого натурального числа 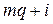 класс
класс  . Поскольку остаток – по-латински residu – переводится на русский язык как вычет, то множество всех классов сравнимых друг с другом по данному модулю
. Поскольку остаток – по-латински residu – переводится на русский язык как вычет, то множество всех классов сравнимых друг с другом по данному модулю  В силу сказанного
В силу сказанного  – множество из
– множество из  и для произвольных
и для произвольных  суммы
суммы  и
и  принадлежат одному классу из
принадлежат одному классу из  так как эти суммы сравнимы друг с другом по модулю
так как эти суммы сравнимы друг с другом по модулю  согласно свойству 2 сравнений (см. теоретический материал к первому разделу). Аналогично, произведения
согласно свойству 2 сравнений (см. теоретический материал к первому разделу). Аналогично, произведения  и
и  лежат в одном классе из
лежат в одном классе из  Å
Å  тот единственный класс
тот единственный класс  из
из  в который попадают все суммы
в который попадают все суммы  и
и  для
для  а произведением
а произведением  – тот класс из
– тот класс из  для произвольных
для произвольных 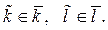
 однозначно определяются умножением представителей классов, то свойства 1 – 5 операций сложения и умножения целых чисел (см. раздел 1) справедливы и в
однозначно определяются умножением представителей классов, то свойства 1 – 5 операций сложения и умножения целых чисел (см. раздел 1) справедливы и в 
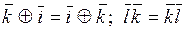 – коммутативность;
– коммутативность; – ассоциативность;
– ассоциативность; ;
; существует единственный класс
существует единственный класс  , очевидно, им является класс
, очевидно, им является класс  =
=  ;
; – дистрибутивность.
– дистрибутивность. в алгебре относят к классу коммутативных колец с единицей и называют кольцом классов вычетов по модулю
в алгебре относят к классу коммутативных колец с единицей и называют кольцом классов вычетов по модулю  , что
, что  . Тогда класс
. Тогда класс  называют обратным к классу
называют обратным к классу  такой класс, что
такой класс, что  Тогда:
Тогда: произведение
произведение  ;
; если
если 
 инъективно и, следовательно, биективно на множестве
инъективно и, следовательно, биективно на множестве  );
);
 поэтому, согласно критерию взаимной простоты целых чисел существуют такие целые
поэтому, согласно критерию взаимной простоты целых чисел существуют такие целые  что
что  Тогда
Тогда  Следовательно,
Следовательно,  обратный к
обратный к  такой, что
такой, что  . Тогда:
. Тогда: ;
; такие, что
такие, что 
 то есть класс
то есть класс  из кольца
из кольца  простое число, то в кольце
простое число, то в кольце  каждый ненулевой класс обратим. Обратный класс также обратим. Произведение обратимых классов есть обратимый класс.
каждый ненулевой класс обратим. Обратный класс также обратим. Произведение обратимых классов есть обратимый класс. состоит из конечного множества элементов, то сложение и умножение можно задавать поэлементно в виде таблиц.
состоит из конечного множества элементов, то сложение и умножение можно задавать поэлементно в виде таблиц.




 и
и  в полном соответствии с теоремой 2.1.
в полном соответствии с теоремой 2.1. , которая каждому натуральному числу
, которая каждому натуральному числу  ставит в соответствие
ставит в соответствие для каждого простого числа
для каждого простого числа 
 для каждого простого числа
для каждого простого числа  и для произвольного натурального
и для произвольного натурального 
 то
то  .
. – каноническое разложение числа
– каноническое разложение числа  то
то .
. Поскольку
Поскольку  то согласно свойству 4 значение
то согласно свойству 4 значение 
 Значит, в кольце
Значит, в кольце  имеется именно 4 обратимых элемента. Непосредственная проверка показывает, что этими классами являются
имеется именно 4 обратимых элемента. Непосредственная проверка показывает, что этими классами являются  .
. и натурального
и натурального  , то
, то 
 -й степени с одной неизвестной называется сравнение вида
-й степени с одной неизвестной называется сравнение вида ,
, .
. числа
числа 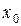 получается верное числовое сравнение, то
получается верное числовое сравнение, то  также будет решением данного сравнения. Поэтому решением алгебраического сравнения можно считать класс вычетов
также будет решением данного сравнения. Поэтому решением алгебраического сравнения можно считать класс вычетов  . Универсальным способом решения алгебраических сравнений является испытание полной системы вычетов по модулю
. Универсальным способом решения алгебраических сравнений является испытание полной системы вычетов по модулю  , то есть целых чисел
, то есть целых чисел  Сравнение будет иметь столько решений, сколько вычетов полной системы ему удовлетворяют.
Сравнение будет иметь столько решений, сколько вычетов полной системы ему удовлетворяют. .
. . Поэтому указанное сравнение имеет два решения:
. Поэтому указанное сравнение имеет два решения: 
 для всех натуральных
для всех натуральных 



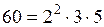 . Согласно свойству 4 функции Эйлера
. Согласно свойству 4 функции Эйлера .
. . Поэтому согласно свойству 2 функции Эйлера
. Поэтому согласно свойству 2 функции Эйлера .
.
 не делится на все простые 2, 3, 5, 7, меньшие 10. Следовательно, 89 – число простое. Поэтому
не делится на все простые 2, 3, 5, 7, меньшие 10. Следовательно, 89 – число простое. Поэтому 
 и
и  составить таблицы сложения и умножения. Найти в этих кольцах пары взаимно обратных по умножению элементов. Указать количество таких пар и сравнить это количество с
составить таблицы сложения и умножения. Найти в этих кольцах пары взаимно обратных по умножению элементов. Указать количество таких пар и сравнить это количество с  и
и  соответственно.
соответственно. Рассмотрим ниже другой путь решения этой задачи.
Рассмотрим ниже другой путь решения этой задачи. имеется
имеется  классов вычетов, взаимно простых с модулем
классов вычетов, взаимно простых с модулем  Прямая проверка показывает, что эти классы составляют множество
Прямая проверка показывает, что эти классы составляют множество 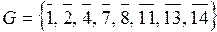 .
. для
для  выглядит как
выглядит как 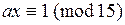 , а из теоремы Эйлера следует, что
, а из теоремы Эйлера следует, что  Умножив сравнение
Умножив сравнение 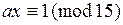 на
на  , получим
, получим  согласно свойствам сравнений. Последовательно вычисляем:
согласно свойствам сравнений. Последовательно вычисляем: , следовательно,
, следовательно,  ;
; , следовательно,
, следовательно,  ;
; ;
; ;
;
 в кольце: а)
в кольце: а) 

 Этот наибольший общий делитель найдем по алгоритму Евклида:
Этот наибольший общий делитель найдем по алгоритму Евклида:  Отсюда легко получается соотношение Безу для
Отсюда легко получается соотношение Безу для 
 Согласно замечанию к лемме 2.1
Согласно замечанию к лемме 2.1  Проверка:
Проверка:
 Поэтому в кольце
Поэтому в кольце  не существует
не существует 