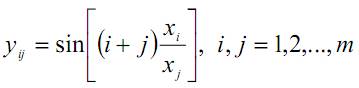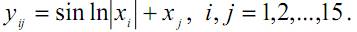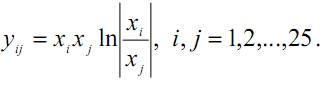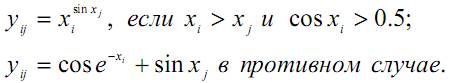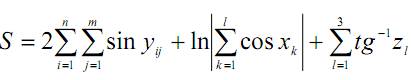ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение
Как определить диапазон голоса - ваш вокал
Игровые автоматы с быстрым выводом
Как цель узнает о ваших желаниях прежде, чем вы начнете действовать. Как компании прогнозируют привычки и манипулируют ими
Целительная привычка
Как самому избавиться от обидчивости
Противоречивые взгляды на качества, присущие мужчинам
Тренинг уверенности в себе
Вкуснейший "Салат из свеклы с чесноком"
Натюрморт и его изобразительные возможности
Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д.
Как научиться брать на себя ответственность
Зачем нужны границы в отношениях с детьми?
Световозвращающие элементы на детской одежде
Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия
Как слышать голос Бога
Классификация ожирения по ИМТ (ВОЗ)
Глава 3. Завет мужчины с женщиной

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
 Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу. Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.
 Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар. Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.
| Доступ к элементам массива
Для доступа к n-ому элементу необходимо написать имя_массива[номер строки] [номер колонки] и работать с ним как с обычной переменной. Примеры доступа к элементам двумерного массива: num [0][1]=100; //записать в элемент num(0,1) число 100 test[1][1]=0,5; // в элемент test(1,1) записать 0,5 test[9][9]=10; // в элемент test(9,9) записать число 10 1.8. Алгоритмы обработки двумерных массивов Программирование вычислительных процессов, содержащих многомерные массивы, основано на использовании вложенных циклических процессов. Поэтому блок-схемы алгоритмов задач на многомерные массивы базируются, как правило, на типовой блок-схеме организации вложенных циклических процессов (см. лаб. работу № 9). Вычисления же реализуется обычно с использованием операторов цикла и, в первую очередь, оператора цикла со спецификацией типа арифметической прогрессии (см. лаб. работу № 9). Программирование вычислительных процессов, содержащих многомерные массивы, рассмотрим на конкретных примерах. 1.8.1. Ввод и вывод матрицы | | | //Ввод матрицы float x[10][10]; cout << "Введите m,n"; cin >>m >> n; for(i=0;i<m;i++) for(j=0;j<n;j++) { cout <<"Введите "x[" << i << "," << j <<"]= "; cin >> x[i][j]; } //Вывод матрицы cout <<"Матрица x:"; for(i=0;i<m;i++) { for(j=0;j<n;j++) cout <<x[i][j]; cout <<"\n"; } |  | | Рис. 11.2. Ввод-вывод матрицы | | | Замечание: если в текущий момент необходимо обрабатывать не все 10 строк и 10 столбцов, то нужно использовать вспомогательные переменные m и n (при этом должны выполнятся условия m≤10 и m≤10); не забудьте предварительно задать значения переменным m и n – с помощью оператора присваивания или использовав оператор ввода). Примечание. Ввод-вывод динамической матрицы отличается от ввода-вывода статической матрицы лишь описанием матрицы. 1.8.2. Заполнение матрицы случайными числами Ниже приведен пример заполнения матрицы 5Х4 случайными числами. int k; int arr[5][4]; //объявление массива 5Х4 – 5 строк 4 колонки for (i=0;i<5;i++) { for(j=0;j<4;j++) { //обработка данных k=rand()%10+1; //вычисление случайного числа в диапазоне 1-10 arr[i][j]=k; //сохранение случайного числа в массиве } } 1.8.3. Определение количество элементов, больших заданного А и расположенных в строках с нечетными номерами | /* Определение количества элементов, больших заданного А и расположенных в строках с нечетными номерами */ #include <stdio.h> #include <math.h> int main ( ) { int i, j, m, n, K; float B [10][10]; float A; //Описание переменных cout <<" Введите число строк и столбцов"; cin >> m >>n; for(i=0; i<m; i++) for(j=0; j<n; j++) { cout <<"Введите "x[" << i << "," << j <<"]= "; cin >> b[i][j]; } cout << "Матрица B:"; for(i=0;i<m;i++) { for(j=0;j<n;j++) cout <<b[i][j]; cout <<"\n"; } cout <<" Введите число A"; cin >> A; K=0; for ( i=1; i<m; i=i+2) for ( j=0; j<n;j++) if( B[i][j]>A) K=K+1; cout << "K = " << K << endl; }//конец main |  | | | | | Рис. 11.3. Ввод-вывод матрицы | | | Таблица 11.3 Таблица соответствия | Переменные в задаче | Имя на языке Си | Тип | Комментарий | | K | K | int | Искомое количество элементов | | B | B | float | Двумерный статический массив | | A | A | float | Заданное число | | - | i | int | Номер строки | | - | | int | Номер столбца |
Тесты: | | | | -3; | 8; | -2; | 10; | 7; | 82; | -4 | | | | | | | | | | | | | 1) | В= | -9; | 0; | -3; | 85; | 3; | 40; | | | A= 4; K=7. | | | | | | | | | -1; | 8; | 7; | -95; | 4; | -5; | | | | | | | | | | | | | | | | -4; | -7; | 8; | 9; | 2; | -8; | -5 | | | | | | | | | | | | | 2) | В= | -2; | 10; | 0; | 9; | -8; | 7; | -5 | | A= 10; K=0. | | | | | | | | | -7; | 6; | -9; | 7; | 0; | -3; | | | | | | | | | | | | 1.8.4. Поиск в матрице строки с максимальной суммой | | | | /* Строка с максимальной суммой*/ #include <stdio.h> int main() { int m, n, nmax, i, j; float max, s, x[10][10]; print("Введите m, n"); scanf("%d %d", &m, &n); for(i=0;i<m;i++) for(j=0;j<n;j++) { printf ("Введите x[%d][%d]=", i, j); scanf ("%f, &x[i][j]); } print ("Матрица x:"); for(i=0;i<m; i++) { for(j=0;j<n; j++) printf("%8.2f',x[i][j]); printf("\n"); } s=0; for(j=0; j<n; j++) s =s+x[0][j]; //Нач. знач. мax - сумма элем. 0-ой стр. max=s; nmax=0; for(i=0;i<m;i++) { s=0; for(j=0;j<n;j++) s+=x[i][j]; //Сумма элем. строк if(max<s) { max=s; nmax=i;} } рrint("Максимальная сумма %.2f в строке %d\n",max,nmax); fflush(stdin); getchar(); return(0); } |  | | Рис. 11.4. Поиск в матрице строки с максимальной суммой | | | 1.8.5. Определение количества строк матрицы, в которых суммы всех элементов отрицательные Определить количество строк матрицы, в которых суммы всех элементов отрицательные. Массив объявить как динамический. | | | | /*Пример обработки двумерного динамического массива*/ include <stdio.h> include <math.h> int main ( ) { int i, j, m, n; float K, S; //Описание переменных puts (" введите n, m"); //Вывод сообщения scanf ("%d %d", &n, &m); //Ввод исх. числа строк и столбцов float**A=new float*[n]; for(i=0; i<n; i++) A[i]=new float[m]; for(i=0; i<n; i++) for(j=0; j<m; j++) { рrint("Введиге A[%d; %d]=", i, j); scanf("%f&A[i] [j]); } K=0; for(i=0; i<n; i++) { S=0; for(j=0; j<m; j++) S=S+A[i] [j]; if(S<0) K=K+1; } printf("%f \n", K); for(i=0; i<n; //Освобождение динамической памяти delete[]A[i]; delete[]A; } | 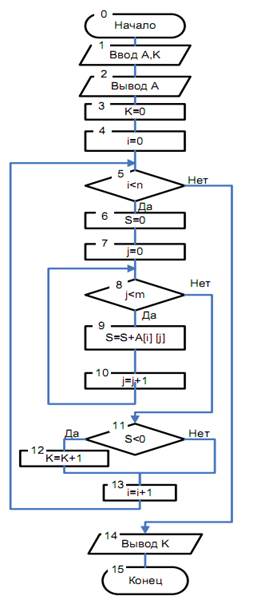 | | Рис. 11.5. Определение количества строк матрицы, в которых суммы всех элементов отрицательные | | | Таблица 11.4 Таблица соответствия | Переменные в задаче | Имя на языке Си | Тип | Комментарий | | S | S | float | Сумма элементов i-той строки | | A | A | float | Двумерный динамический массив | | K | K | float | Количество искомых строк | | - | n | int | Количество всех строк в матрице | | - | m | int | Количество столбцов | | - | i | int | Номер строки | | - | | int | Номер столбца | Тесты: | | | | -3; | -2; | 2; | 6; | -3; | | | | | | | | | | | | | | | 1) | A= | 6; | 7; | -1; | 20; | -4; | | | | K=2. | | | | | | | | | -4; | -2; | -3; | 6; | -1; | | | | | | | | | | | | | | | | | -4; | -2; | 4; | 6; | 4; | | | | | | | | | | | | | | | 2) | A= | 3; | 5; | 7; | 2; | 0; | | | | K=0. | | | | | | | | | 5; | 0; | -2; | 9; | 0; | | | | | | | | | | | | | 1.8.6. Определение, есть ли в матрице столбец, содержащий хотя бы один нулевой элемент | | | | #include <stdio.h> #include <conio.h> int main() { int m,n,i,j,t,w; float x[10][10]; puts("Введите m,n"); scanf("%d %d",&m,&n); for(i=0;i<m;i++) for(j=0;j<n;j++) { printf("Введите x[%d][%d]=",i, j); scanf("%f', &x[i][j]); } puts("Матрица x:"); for(i=0;i<m;i++) for(j=0;j<n;j++) printf("%8.2f',x[i][j]); printf('W'); } t=1; j=0; //Столбец еще не найден while(j<n && t) { w=1; i=0; //В столбце не найден элем., равный нулю while(i<m && w) if(x[i][j]==0) w=0; else i++; if(w) j++ //В столбце нет равного 0 элем. else t=0; // В столбце есть равный 0 элем. } if(t) рrintf("Нет\n"); else printf("Есть %d %d\n",ij); getch(); return(0); } |  | | Рис. 11.6. Определение, есть ли в матрице столбец, содержащий хотя бы один нулевой элемент | | | При решении задачи используются две вспомогательные переменные t и w: | t = |   | 1, если столбец не найден; | | 0, если столбец найден. | | | | | w = | | 1, в столбце не найден элемент, равный нулю | | 0, в столбце найден элемент, равный нулю. | 1.8.7. Обработка элементов квадратных матриц относительно главной и побочной диагоналей | | | | /* Фомирование матрицы */ #include <stdio.h> int main() { const m=10; int i,j,N; int x[m][m]; /* Обнуление матрицы */ for(i=0;i<m;i++) for(j=0;j<m;j++) x[i][j]=0; рrintf("Номер варианта?"); scanf("%d",&N); рrintf("Вариант %d:\n",N); switch(N) { case 1:{ /* Вариант 1 */ for(i=0;i<m;i++) for(j=0;j<i+1;j++) x[i][j]=i-j+1; break;} case 2:{ /* Вариант 2 */ for(j=0;j<m;j++) for(i=j;i<m;i++) x[i][j]=j+1; break; } case 3: { /* Вариант 3 */ for(i=0;i<m;i++) for(j=i;j<m;j++) x[i][j]=i+1; break; } case 4: { /* Вариант 4 */ for(i=0;i<m;i++) for(j=i;j<m;j++) x[i][j]=j-i+1; break; } case 5:{ /* Вариант 5 */ for(i=0;i<m;i++) for(j=0;j<m;j++) x[i][j]=i+1; break; } case 6: { /* Вариант 6 */ for(i=0;i<m;i++) for(j=i;j<m;j++) if (i==j) x[i][j]=1; else x[i][j]=2; break; } case 7:{ /* Вариант 7 */ for(i=0;i<m;i++) for(j=0;j<i+1;j++) x[i][j]=1; break; } case 8:{ /* Вариант 8 / for(i=0;i<m;i++) for(j=0;j<i+1;j++) x[i][j]=(i-j+1)*(i-j+1); break; } case 9: { /* Вариант 9 */ for(j=0;j<m;j++) for(i=j;i<m;i++) x[i][j]=(j+1)*(j+1); break; } case 10:{ /* Вариант 10 */ for(j=0;j<m;j++) for(i=0;i<m;i++) if((i+j)%2==0) x[i][j]=1; else x[i][j]=0; break; } case 11: /* Вариант 11*/ for(i=0;i<m;i++) for(j=m-i-1;j<m;j++) x[i][j]=1; break; } case 12:{ /* Вариант 12 */ for(i=0;i<m;i++) for(j=0;j<m;j++) x[i][j]=(i+1)*(i+1); break; } case 13:{ /* Вариант 13 */ for(i=0;i<m;i++) for(j=m-i-1;j<m;j++) if (i+j==m-1) x[i][j]=1; else x[i][j]=2; break; } case 14:{ /* Вариант 14 */ for(i=0;i<m;i++) for(j=i;j<m;j++) x[i][j]=(j-i+1)*(j-i+1); break;} } // Вывод матрицы for(i=0;i<m;i++) { for(j=0;j<m;j++) printf("%4d",x[i][j]); printf("\n"); } fflush(stdin); getchar(); return(0); } | | | Рис. 11.7. Обработка элементов квадратных матриц относительно главной и побочной диагоналей | | | 2. ЗАДАНИЕ 2.1. Изучить теоретические сведения. 2.2. Разобрать и выполнить примеры к данной лабораторной работе. 2.3. Написать и отладить семь программ на языке С++. 2.4. Задания для выполнения на занятиях 2.4.1. Задание 1. Вычисление сумм, количеств и произведений элементов матрицы 2.4.1.1. Условие задания В каждой из задач данного раздела (табл. 11.1) предполагается, что задана матрица размером NхM. Программа должна: 1) вводить размерность и элементы матрицы; 2) вводить некоторые дополнительные числа; 3) выполнять действия в соответствии с условием задачи; 4) выводить исходные данные и результаты вычислений. Исходные данные для отладки программы выбрать самостоятельно. Массив объявить как статический. Таблица 11.1 Варианты заданий | № | Задание | | Вычислить сумму положительных элементов, расположенных в столбцах с четными номерами. | | Вычислить произведение отрицательных элементов, расположенных в строках с нечетными номерами. | | Вычислить сумму квадратов элементов из интервала [A,B], расположенных в строках с четными номерами. | | Определить количество элементов, больших заданного А и расположенных в строках с нечетными номерами. | | Вычислить сумму элементов, меньших заданного В и расположенных в столбцах с номерами, кратными 3. | | Вычислить произведение положительных элементов, расположенных в строках с номерами, кратными 4. | | Вычислить сумму квадратов отрицательных элементов, расположенных в столбцах с четными номерами. | | Определить количество элементов, непринадлежащих промежутку (A,B) и расположенных в столбцах с нечетными номерами. | | Вычислить сумму элементов, неменьших заданного D и расположенных в строках с четными номерами. | | Вычислить произведение элементов, небольших заданного F и расположенных в строках с нечетными номерами. | | Вычислить сумму квадратов положительных элементов, расположенных в столбцах с номерами, кратными 3. | | Определить количество отрицательных элементов, расположенных в строках с номерами, кратными 3. | | Вычислить сумму элементов, принадлежащих промежутку [A,B) и расположенных в столбцах с четными номерами. | | Вычислить произведение элементов, больших заданно го Х и расположенных в столбцах с нечетными номерами. | | Вычислить сумму квадратов элементов, меньших Y и расположенных в строках с нечетными номерами. | | Определить, сколько положительных элементов расположено в строках с нечетными номерами. | | Вычислить сумму отрицательных элементов, расположенных в столбцах с номерами, кратными 3. | | Вычислить произведение элементов, непринадлежащих интервалу (X, Y) и расположенных в строках с номерами, кратными 3. | | Вычислить сумму квадратов элементов, неменьших заданного Z и расположенных в столбцах с четными номерами. | | Найти количество элементов, небольших S и расположенных в строках с нечетными номерами. | | Вычислить сумму положительных элементов, расположенных в строках с четными номерами. | | Вычислить произведение отрицательных элементов, расположенных в строках с нечетными номерами. | | Вычислить сумму элементов, принадлежащих промежутку [X, Y] и расположенных в столбцах с номерами, кратными 3. | | Определить, сколько элементов, больших заданного Т расположено в строках с номерами, кратными 3. | | Вычислить сумму квадратов элементов, меньших заданного D и расположенных в столбцах с четными номерами. | | Вычислить произведение положительных элементов, рас положенных в столбцах с нечетными номерами. | | Вычислить сумму квадратов отрицательных элементов, расположенных в строках с четными номерами. | | Вычислить количество элементов, не принадлежащих промежутку [B,C) и расположенных в строках с нечетными номерами. | | Вычислить сумму элементов, по абсолютной величине больших К и расположенных в столбцах с номерами, кратными 3. | | Вычислить произведение элементов, по абсолютной величине меньших G и расположенных в строках с номерами, кратными 3. | 2.4.1.2. Пример для варианта 30 Вычислить произведение элементов, по абсолютной величине меньших G и расположенных в строках с номерами, кратными 3. 2.4.1.3. Программа //Лабораторная работа № 11 //Задание 1 //Вариант 30 //Выполнила Петрова А.А. /* Вычисление произведения элементов, по абсолютной величине меньших G и расположенных в строках с номерами, кратными 3 */ #include <stdio.h> #include <conio.h> #include <math.h> #include <iostream.h> int main() { int i, j, m, n; float B[10][10]; float G,P; //Описание переменных cout <<" Введите число строк m ";cin >> m; cout <<" Введите число столбцов n "; cin >> n; for(i=0; i<m; i++) for(j=0; j<n; j++) { cout <<"Введите B[" << i << "," << j <<"]= "; cin >> B[i][j]; } cout <<" Введите число G "; cin >> G; //Контрольный вывод исходных данных cout <<"Число строк m = " << m << endl; cout <<"Число столбцов n = "<< n << endl; cout << "Матрица B:" << endl; for(i=0;i<m;i++) { for(j=0;j<n;j++) cout <<B[i][j] << " "; cout <<"\n"; } cout <<"Число G = "<< G << endl; P=1;//Правило вычисления произведений for ( i=1; i<m; i=i+3) for ( j=0; j<n;j++) if( fabs(B[i][j])<G) P=P* B[i][j]; cout << "Искомое произведение P = " << P << endl; cout << "Нажмите любую клавишу..." ; getch(); return 0; }//конец main 2.4.1.4. Тестирование 
2.4.2. Задание 2. Выполнение вычислений в строках и столбцах матрицы 2.4.2.1. Условие задания В каждой из задач данного раздела (табл. 11.2) предполагается, что задана матрица размером NxM. Программа должна: – вводить размерность и элементы матрицы; – вводить некоторые дополнительные числа; – выполнять действия в соответствии с условием задачи; –выводить исходные данные и результаты вычислений. Исходные данные для отладки программы выбрать самостоятельно. Массив объявить как динамический. Таблица 11.2 Варианты заданий | № | Задание | | В каждой нечетной по номеру строке матрицы найти минимальный элемент и вычислить произведение этих элементов. | | В каждом столбце матрицы найти произведение положительных элементов и вычислить сумму этих произведений. | | Определить количество столбцов матрицы, в которых больше трех положительных элементов. | | Определить количество строк матрицы, в которых суммы всех элементов отрицательные. | | В каждой строке матрицы найти самый левый отрицательный элемент и вычислить произведение этих элементов. | | Определить количество строк матрицы, в которых нет положительных элементов. | | Заменить в матрице элементы последней строки на произведение элементов соответствующих столбцов. | | В каждом столбце матрицы найти минимальный элемент и вычислить сумму этих элементов. | | В каждой строке матрицы найти произведение отрицательных элементов и вычислить сумму этих произведений. | | Заменить в матрице элементы предпоследней строки на минимальные элементы соответствующих столбцов. | | Определить количество строк матрицы, в которых произведение положительных элементов больше заданного В. | | В каждой строке матрицы найти самый правый положительный элемент и вычислить сумму этих элементов. | | Определить количество столбцов матрицы, в которых нет положительных элементов. | | Заменить в матрице элементы последнего столбца на суммы элементов соответствующих строк. | | В каждом столбце матрицы найти максимальный элемент и вычислить произведение этих элементов. | | В каждой четной по номеру строке матрицы найти минимальный элемент и вычислить сумму этих элементов. | | В каждом столбце матрицы найти сумму отрицательных элементов и вычислить произведение этих сумм. | | Определить количество строк матрицы, в которых произведение элементов положительное. | | Заменить в матрице элементы второго столбца на суммы положительных элементов соответствующих строк. | | В каждом столбце матрицы найти первый отрицательный элемент и вычислить сумму этих элементов. | | Определить количество строк матрицы, в которых все элементы отрицательные. | | Заменить в матрице элементы предпоследнего столбца на суммы элементов соответствующих строк. | | В каждом нечетном по номеру столбце матрицы найти минимальный элемент и вычислить произведение этих элементов. | | В каждой строке матрицы найти сумму положительных элементов и вычислить произведение этих сумм. | | Определить количество столбцов матрицы, в которых все элементы положительные. | | Заменить в матрице элементы предпоследней строки на количество положительных элементов соответствующих столбцов. | | В каждом столбце матрицы найти самый нижний положительный элемент и вычислить произведение этих элементов. | | Определить количество строк матрицы, в которых нет положительных элементов. | | Определить количество столбцов матрицы, в которых все элементы нулевые. | | В каждом столбце матрицы найти минимальный элемент и вычислить сумму этих элементов. | 2.4.2.2. Пример для варианта 30 В каждом столбце матрицы найти минимальный элемент и вычислить сумму этих элементов. 2.4.2.3. Программа //Лабораторная работа № 11 //Задание 2 //Вариант 30 //Выполнила Макова А.А /* Вычисление сумм элементов столбцов и поиск минимальных элементов столбцов */ #include <stdio.h> #include <conio.h> #include <math.h> #include <iostream.h> int main() { int i, j, m, n; float B[10][10]; float BMIN[10]; float BS[10]; float S,MIN; //Описание переменных cout <<" Введите число строк m ";cin >> m; cout <<" Введите число столбцов n "; cin >> n; for(i=0; i<m; i++) for(j=0; j<n; j++) { cout <<"Введите B[" << i << "," << j <<"]= "; cin >> B[i][j]; } S=0;//Правило накопления сумм // Вычисление сумм элементов столбцов for ( j=0; j<n;j++) { S=0; for ( i=0; i<m; i++) S=S +B[i][j]; BS[j]= S; } //Поиск минимальных элементов столбцов for ( j=0; j<n;j++) { MIN=B[0][j] ; for ( i=1; i<m; i++) if (MIN > B[i][j]) MIN =B[i][j] ; BMIN[j]= MIN; } //Контрольный вывод исходных данных cout <<"Число строк m = " << m << endl; cout <<"Число столбцов n = "<< n << endl; cout << "Матрица B:" << endl; for(i=0;i<m;i++) { for(j=0;j<n;j++) cout <<B[i][j] << " "; cout <<"\n"; } cout << "Массив минимальных элементов столбцов BMIN:" << endl; for(j=0;j<n;j++) cout <<BMIN[j] << " "; cout << "\nМассив сумм столбцов BS:" << endl; for(j=0;j<n;j++) cout <<BS[j] << " "; cout << "\nНажмите любую клавишу..." ; getch(); return 0; }//конец main Замечание: накопление сумм столбцов и поиск минимальных элементов столбцов можно совместить. Фрагмент программы, реализующий указанное замечание приведен ниже for ( j=0; j<n;j++) { S=B[0][j]; MIN=B[0][j] ; for ( i=1; i<m; i++) {if (MIN > B[i][j]) MIN =B[i][j] ; S=S +B[i][j]; } BS[j]= S; BMIN[j]= MIN; } Результат, естественно будет тем же. 2.4.2.4. Тестирование 
2.4.3. Задание 3. Дополнительные задачи 2.4.3.1. Условие задания Таблица 11.3 Варианты заданий | № | Задание | | Дана целочисленная прямоугольная матрица. Определить: – количество строк, не содержащих ни одного нулевого элемента; – максимальное из чисел, встречающихся в заданной матрице более одного раза. | | Дана целочисленная прямоугольная матрица. Определить количество столбцов, не содержащих ни одного нулевого элемента. Характеристикой строки целочисленной матрицы назовем сумму ее положительных четных элементов. Переставляя строки заданной матрицы, расположить их в соответствии с ростом характеристик. | | Дана целочисленная прямоугольная матрица. Определить: – количество столбцов, содержащих хотя бы один нулевой элемент; – номер строки, в которой находится самая длинная серия одинаковых элементов. | | Дана целочисленная квадратная матрица. Определить: – произведение элементов в тех строках, которые не содержат отрицательных элементов; – максимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы. | | Дана целочисленная квадратная матрица. Определить: – сумму элементов в тех столбцах, которые не содержат отрицательных элементов; – минимум среди сумм модулей элементов диагоналей, параллельных побочной диагонали матрицы. | | Дана целочисленная прямоугольная матрица. Определить: – сумму элементов в тех строках, которые содержат хотя бы один отрицательный элемент; – номера строк и столбцов всех седловых точек матрицы. Примечание. Матрица А имеет седловую точку А1, если А1 является минимальным элементом в i-й строке и максимальным в j-м столбце. | | Для заданной матрицы размером 8 на 8 найти такие k, что k-я строка матрицы совпадает с k-м столбцом. Найти сумму элементов в тех строках, которые содержат хотя бы один отрицательный элемент. | | Характеристикой столбца целочисленной матрицы назовем сумму модулей его отрицательных нечетных элементов. Переставляя столбцы заданной матрицы, расположить их в соответствии с ростом характеристик. Найти сумму элементов в тех столбцах, которые содержат хотя бы один отрицательный элемент. | | Соседями элемента Ау в матрице назовем элементы Akl с i - 1 <= k <= j-1 <= 1 <= (k, 1) <> (i, j). Операция сглаживания матрицы дает новую матрицу того же размера, каждый элемент которой получается как среднее арифметическое имеющихся соседей соответствующего элемента исходной матрицы. Построить результат сглаживания заданной вещественной матрицы размером 10 на 10. В сглаженной матрице найти сумму модулей элементов, расположенных ниже главной диагонали. | | Элемент матрицы называется локальным минимумом, если он строго меньше всех имеющихся у него соседей. Подсчитать количество локальных минимумов заданной матрицы размером 10 на 10. Найти сумму модулей элементов, расположенных выше главной диагонали. | | Коэффициенты системы линейных уравнений заданы в виде прямоугольной матрицы. С помощью допустимых преобразований привести систему к треугольному виду. Найти количество строк, среднее арифметическое элементов которых меньше заданной величины. | | Уплотнить заданную матрицу, удаляя из нее строки и столбцы, заполненные нулями. Найти номер первой из строк, содержащих хотя бы один положительный элемент. | | Осуществить циклический сдвиг элементов прямоугольной матрицы на n элементов вправо или вниз (в зависимости от введенного режима), n может быть больше количества элементов в строке или столбце. | | Осуществить циклический сдвиг элементов квадратной матрицы размерности М х N вправо на k элементов таким образом: элементы 1-й строки сдвигаются в последний столбец сверху вниз, из него - в последнюю строку справа налево, из нее — в первый столбец снизу вверх, из него - в первую строку; для остальных элементов - аналогично. | | Дана целочисленная прямоугольная матрица. Определить номер первого из столбцов, содержащих хотя бы один нулевой элемент. Характеристикой строки целочисленной матрицы назовем сумму ее отрицательных четных элементов. Переставляя строки заданной матрицы, расположить их в соответствии с убыванием характеристик. | | Упорядочить строки целочисленной прямоугольной матрицы по возрастанию количества одинаковых элементов в каждой строке. Найти номер первого из столбцов, не содержащих ни одного отрицательного элемента. | | Путем перестановки элементов квадратной вещественной матрицы добиться того, чтобы ее максимальный элемент находился в левом верхнем углу, следующий по величине — в позиции (2,2), следующий по величине - в позиции (3,3) и т. д., заполнив таким образом всю главную диагональ. Найти номер первой из строк, не содержащих ни одного положительного элемента. | | Дана целочисленная прямоугольная матрица. Определить: – количество строк, содержащих хотя бы один нулевой элемент; – номер столбца, в котором находится самая длинная серия одинаковых элементов. | | Дана целочисленная квадратная матрица. Определить: – сумму элементов в тех строках, которые не содержат отрицательных элементов; – минимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы. | | Дана целочисленная прямоугольная матрица. Определить: – количество отрицательных элементов в тех строках, которые содержат хотя бы один нулевой элемент; – номера строк и столбцов всех седловых точек матрицы. Примечание. Матрица А имеет седловую точку Ауесли Ауявляется минимальным элементом в i-й строке и максимальным в j-м столбце | | Дана целочисленная квадратная матрица. Определить: – сумму элементов в тех строках, которые не содержат отрицательных элементов; – номер столбца, в котором находится самая длинная серия одинаковых элементов. | | Дана целочисленная прямоугольная матрица. Определить: – количество строк, содержащих хотя бы один нулевой элемент; – максимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы. | | Дана целочисленная прямоугольная матрица. Определить: – сумму элементов в тех строках, которые содержат хотя бы один отрицательный элемент; – минимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы. | | Дана целочисленная квадратная матрица. Определить: – сумму элементов в тех строках, которые не содержат отрицательных элементов; – максимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы. | | Уплотнить заданную матрицу, удаляя из нее строки и столбцы, заполненные единицами. Найти номер первой из строк, содержащих хотя бы один отрицательный элемент. | | Дана целочисленная прямоугольная матрица. Определить: – количество строк, содержащих хотя бы один единичный элемент; – номер столбца, в котором находится самая длинная серия одинаковых элементов. | | Дана целочисленная квадратная матрица. Определить: – произведение элементов в тех строках, которые не содержат отрицательных элементов; – максимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы. | | Дана целочисленная прямоугольная матрица. Определить: – количество положительных элементов в тех строках, которые содержат хотя бы один нулевой элемент; – номера строк и столбцов всех седловых точек матрицы. Примечание. Матрица А имеет седловую точку Ауесли Ауявляется минимальным элементом в i-й строке и максимальным в j-м столбце | | Дана целочисленная прямоугольная матрица. Определить: – количество строк, содержащих хотя бы один отрицательный элемент; – минимум среди сумм элементов диагоналей, параллельных главной диагонали матрицы. | | Дана целочисленная квадратная матрица. Определить: – сумму элементов в тех строках, которые не содержат положительных элементов; – номер столбца, в котором находится самая длинная серия одинаковых элементов. | 2.4.3.2. Пример для варианта 30 Дана целочисленная квадратная матрица. Определить: – сумму элементов в тех строках, которые не содержат положительных элементов; – номер столбца, в котором находится самая длинная серия одинаковых элементов. 2.4.3.3. Программа //Лабораторная работа № 11 /* Вычисление суммы элементов, и нахождение номера столбца */ //Задание 3 //Вариант 30 //Выполнила Лебедева К.К. #include <stdio.h> #include <conio.h> #include <math.h> #include <iostream.h> int main() { int i, j, m,k,n,K,S,max, dlin; int B[10][10], ser[10]; //Описание переменных cout <<" Введите число строк и столбцов m ";cin >> m; for(i=0; i<m; i++) for(j=0; j<m; j++) { cout <<"Введите B[" << i << "," << j <<"]= "; cin >> B[i][j]; } //Контрольный вывод исходных данных cout <<"Число строк m = " << m << endl; cout <<"Число столбцов m = "<< m << endl; cout << "Матрица B:" << endl; for(i=0;i<m;i++) { for(j=0;j<m;j++) cout <<B[i][j] << " "; cout <<"\n"; } //Вычисление суммы элементов в тех строках, //которые не содержат положительных элементов for (i=0; i<m; i++) { S=0;K=0; for (j=0; j<m;j++) {if (B[i][j]<0){K = K +1;S = S + B[i][j];} else {cout << "Строка " << i << " содержит положительные элементы" << endl; break; } } if (K==m) cout << "Строка " << i << " Сумма элементов = " << S<< endl; } //Определение номера столбца, в котором находится самая длинная серия одинаковых элементов for (k=0; k<m;k++) {dlin=1; for (i=0; i<m-1;i++) {n=1; for (j=i+1; j<m;j++) if (B[i][k]== B[j][k]) n = n +1; if (n>dlin) dlin = n; } ser[k] = dlin; } max = ser[0];k=0; for (i=1; i<m;i++) if (max < ser[i]) {max=ser[i]; k=i;} cout << "\nДлинная серия равна " << max <<endl; cout << "\nи находится в "<< k<< " столбце"<< endl; cout << "\nНажмите любую клавишу..." ; getch(); return 0; }//конец main 2.4.3.4. Тестирование 
2.4.4. Задание 4. Перестановки строк или столбцов матрицы 2.4.4.1. Условие задания Разработать алгоритм и программу перестановки строк или столбцов матрицы. В каждой задаче задана прямоугольная матрица размeром МхN. Требуется составить и отладить программу, которая вводит и печатает все исходные данные, осуществляет перестановку строк или столбцов матрицы в соответствии с условием задачи и печатает полученную матрицу. Для отладки программы самостоятельно подберите необходимые наборы исходных данных. Задачу выбрать из таблицы 3 в соответствии со своим вариантом. Таблица 11.4 Варианты заданий | № | Задание | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность D1≥D2≥ … ≥ Di ≥ …≥ DN, где Di – максимальное значение элементов i-ой строки (i=1,2,…,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность С1<С2<^ < Cj <.. .< См, где Cj- минимальное значение элементов j-ого столбца (j=1,2,.. .,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность F1>F2> ... > Fi > .. .> FN, где Fi - сумма элементов i-ой строки (i=1,2,.. .,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность P1<P2<^ < Pj <.. .< PM, где Pj- произведение элементов j-ого столбца (j=1,2,.. .,M). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность K1>K2>_ >Kj >.. .> KM, где Kj- количество положительных элементов j-ого столбца G=1,2,-.,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность L1<L2< ... < Li <.. .< LN, где Li - количество отрицательных элементов i-ой строки (i=1,2,.. .,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность R1>R2>^ >Rj >.. .> RM, где Rj- количество нулевых элементов j-ого столбца (j=1,2,.. .,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность S1<S2< ... < Si <.. .< SN, где Si - сумма абсолютных значений элементов i-ой строки (i=1,2,_,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность T1<T2<_ < Tj <.. .< TM, где Tj- максимальное значение элементов j-ого столбца (j=1,2,.. .,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность Z1>Z2> ... > Zi > .. .> ZN, где Zi - максимальное значение элементов i-ой строки (i=1,2, ,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность T^T^... < Tj <.. .< TM, где Tj- сумма элементов j-ого столбца (j=1,2,_,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность X1>X2> ... > Xi > .. .> XN, где Xi - произведение элементов i-ой строки (i=1,2,.. .,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность H^H^... < Hj <.. .< HM, где Hj- количество положительных элементов j-ого столбца (j=1,2,...,M). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность A^A^... >Aj >_> AM, где Aj- количество отрицательных элементов j-ого столбца (j=1,2,..,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность B1<B2< ... < Bi <_< BN, где Bi - количество нулевых значений элементов i-ой строки (i=1,2,_,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность С1<С2<_ < Cj <_< CM, где Cj- сумма абсолютных значений элементов j-ого столбца (j=1,2,_,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность Y1<Y2< _ < Yi <_< YN, где Yi - максимальное элементов i-ой строки (i=1,2,_,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность E1>E2>_ >Ej >_> EM, где Ej- минимальное значение элементов j-ого столбца (j=1,2,_,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность F1<F2< _ < Fi <_< FN, где Fi - сумма элементов i-ой строки (i=1,2,_,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность G1>G2>^ >Gj >.. .> GM, где Gj- произведение элементов j-ого столбца (j=1,2,.. .,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность V1>V2> ... > Vi > .. .> VN, где Vi - количество положительных элементов i-ой строки (i=1,2,...,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность Q<C2<... < Cj <.. .< CM, где Cj- количество отрицательных значений элементов j-ого столбца (j=1,2,...,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность K1>K2> ... > Ki > .. .> KN, где Ki - количество нулевых элементов i-ой строки (i=1,2, ,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность P^P^... < Pj <.. .< PM, где Pj- сумма элементов j-ого столбца (j=1,2,.. .,M). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность X^X^... >Xj >.. .> XM, где Xj- максимальное значение элементов j-ого столбца (j=1,2,_,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность Y1<Y2< ... < Yi <.. .< YN, где Yi - минимальное значение элементов i-ой строки (i=1,2, ,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность ЩХЦ^... >Uj >.. .> UM, где Uj- среднее значение не нулевых элементов j-ого столбца (j=1,2,_,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность V1<V2< _ < Vi <_< VN, где Vi - произведение не нулевых элементов i-ой строки (i=1,2,_,N). | | В матрице размером M*N переставить столбцы таким образом, чтобы получилась последовательность W1<W2<_ < Wj <_< WM, где Wj- количество положительных значений элементов j-ого столбца (j=1,2,_,M). | | В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность Z1≥Z2≥ … ≥ Zi ≥ …≥ ZN, где Zi – количество отрицательных элементов i-ой строки (i=1,2,…,N). | 2.4.4.2. Пример для варианта 30 В матрице размером M*N переставить строки таким образом, чтобы получилась последовательность Z1≥Z2≥ … ≥ Zi ≥ …≥ ZN, где Zi – количество отрицательных элементов i-ой строки (i=1,2,…,N). 2.4.4.3. Программа 2.4.4.4. Тестирование 2.5. Домашние задания 2.4.5. Задание 5. Вычисление элементов матрицы 2.4.5.1. Условие задания Составить программу для вычисления элементов матрицы Y по известным элементам вектора X. Таблица 11.5 Варианты заданий 2.4.5.2. Пример для варианта 30 Составить программу для вычисления элементов матрицы Y по известным элементам вектора X. 
2.4.5.3. Программа //Лабораторная работа № 11 /* Формирование матрицы из вектора */ #include <stdio.h> #include <conio.h> #include <math.h> #include <iostream.h> int main() { int i, j, m, n; float X[10],Y[10][10]; //Описание переменных cout <<" Введите число строк m ";cin >> m; cout <<" Введите число столбцов n "; cin >> n; for(i=0; i<m; i++) { cout <<"Введите X[" << i << "]= "; cin >> X[i]; } //Контрольный вывод исходных данных cout <<"Число строк m = " << m << endl; cout <<"Число столбцов n = "<< n << endl; cout << "Вектор X:" << endl; for(i=0;i<m;i++) cout <<X[i] << " "; cout <<"\n"; //Формирование матрицы Y for(i=0; i<m; i++) { for ( j=0; j<n; j++) { if (sin(X[i]) <= sin(X[j])) Y[i][j] = sin((i-j)*X[i]); else Y[i][j] = i*cos(X[j]); } } //Вывод матрицы Y cout << "Матрица Y:" << endl; for(i=0;i<m;i++) { for(j=0;j<n;j++) cout <<Y[i][j] << " "; cout <<"\n"; } cout << "Нажмите любую клавишу..." ; getch(); return 0; }//конец main 2.4.5.4. Тестирование 
2.4.6. Задание 6. Вычисление суммы элементов матрицы 2.4.6.1. Условие задания Составить программу для вычисления величины S по формуле. Таблица 11.6 Варианты заданий
©2015 www.megapredmet.ru Все права принадлежат авторам размещенных материалов. |