 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Численное решение задачи Коши 12
Лабораторная работа №5 «Численное дифференцирование и решение дифференциальных уравнений » Волгоград 2012
СОДЕРЖАНИЕ 1. Цель работы.. 4 2. Краткие теоретические сведения. 4 3. Примеры программной реализации рассмотренных методов. 8 4. Задание к выполнению... 11 5. Контрольные вопросы.. 12 6. Рекомендуемая литература.. 12
Цель работы: научиться численно решать дифференциальные уравнения путем написания специализи-рованных программ на языке высокого уровня. Краткие теоретические сведения. Дифференциальные уравнения являются одним из основных математических понятий, наиболее широко применяемых при решении практических задач. Причина этого состоит в том, что при исследовании физических процессов, решении различных прикладных задач, как правило, не удается непосредственно найти законы, связывающие величины, характеризующие исследуемые явления. Обычно легче устанавливаются зависимости между теми же величинами и их производными или дифференциалами. Соотношения такого рода и называются дифференциальными уравнениями. Решение задачи исследования физического явления можно разделить на два этапа: Составление дифференциального уравнения, которое при определенных предположениях описывает сущность рассматриваемого явления. Нахождение решения дифференциального уравнения, то есть функциональной зависимости между величинами, характеризующими исследуемое физическое явление. Возможности и правила составления дифференциальных уравнений определяются знанием законов той области науки, с которой связана природа изучаемой задачи. Так, например, в механике могут использоваться законы Ньютона, в теории электрических цепей – законы Кирхгофа, в теории скоростей химических реакций – закон действия масс и так далее. Для нахождения приближенного решения уравнений применяются: аналитические методы – дающие приближенное решение дифференциального уравнения в виде аналитического выражения; графические методы – дающие приближенное решение в виде графика; численные методы – дающие приближенное решение в виде таблицы. Следует отметить, что приведенная классификация методов приближенного интегрирования является в известной мете условной. Так, например, графический метод ломаных Эйлера дает одновременно способ численного решения дифференциального уравнения. Численное решение задачи Коши Пусть необходимо найти решение уравнения
с начальным условием
Такая задача называется задачей Коши. Численные методы решения задачи (6.1) позволяют найти искомую функцию y(x) лишь приближенно в отличие от точных методов решения. Но при этом численные методы дают возможность приближенно решать многие из задач, точные решения которых аналитическими методами, найдены, не могут. Численное решение задачи (6.1) ищется на интервале [x0, X] левый конец которого x0 задан, а правый конец X может либо задан, либо определен в процессе расчетов некоторым условием. Искомое приближенное решение ищется в отдельных точках x1, x2, ….xk, …. , интервала, называемых узлами сетки, в виде последовательности векторов Y1, Y2, …, Yk,…, приближенно равных векторам , определяемым точным решением Y(x). Полученные результаты заносят в таблицу, которую и называют численным решением задачи Коши. Если на плоскости xOy построить точки таблицы и соединить их отрезками, получится так называемая ломаная Эйлера. Она будет приближением интегральной кривой y=j(x).
Рисунок 5.1. Ломаная Эйлера и интегральная кривая точного решения. Расстояние между соседними узлами называется шагом интегрирования h: h=xk+1-xk. Шаг может быть задан заранее (интегрирование с постоянным шагом) или может меняться в ходе вычислений. Чаще всего:
Метод Эйлера Разложим искомую функцию
Такой метод решения обыкновенных дифференциальных уравнений называется методом Эйлера. Геометрически метод Эйлера означает, что на каждом шаге мы аппроксимируем решение (интегральную кривую) отрезком касательной, проведенной к графику решения в начале интервала.
Рисунок 5.2. Геометрический смысл метода Эйлера. Точность метода невелика и имеет порядок h. Говорят, что метод Эйлера – метод первого порядка, то есть его точность растет линейно с уменьшением шага h. Существуют различные модификации метода Эйлера, позволяющие увеличить его точность. Все они основаны на том, что производную, вычисленную в начале интервала, заменяют на среднее значение производной на данном интервале. Среднее значение производной можно получить (конечно же только приближенно) различными способами. Можно, например, оценить значение производной в середине интервала
Можно также оценить среднее значение производной на интервале
Такие модификации метода Эйлера имеет уже точность второго порядка. Методы Рунге - Кутта Оценку значения производной можно улучшить, увеличивая число вспомогательных шагов. На практике наиболее распространенным методом решения обыкновенных дифференциальных уравнений является метод Рунге-Кутты четвертого порядка. Для оценки значения производной в этом методе используется четыре вспомогательных шага. Формулы метода Рунге-Кутты следующие
Перечисленные методы можно применять и для решения систем дифференциальных уравнений. Поскольку многие дифференциальные уравнения высших порядков могут быть сведены заменой переменных к системе дифференциальных уравнений первого порядка, рассмотренные методы могут быть использованы и для решения дифференциальных уравнений порядка выше первого. Таким образом, различают три основных типа задач для обыкновенных дифференциальных уравнений : задачи Коши, краевые задачи и задачи на собственные значения. Задача Коши или задача с начальными условиями имеет дополнительные условия в виде задания значений всех функций в одной и той же точке. Эти условия можно рассматривать как задание координат начальной точки интегральной кривой в n- мерном пространстве. Методы решения задач можно разделить на точные, приближенные и численные. К точным относят методы, позволяющие выразить решение дифференциального уравнения через элементарные функции. Эти методы изучаются в курсе дифференциального исчисления. Нахождение точного решения задачи облегчает качественное исследование этого решения и дальнейшие действия с ним. Однако классы уравнений, для которых разработаны методы получения точных решений сравнительно узки и охватывают только малую часть возникающих на практике задач. Приближенными называются методы, в которых решение получается как предел некоторой последовательности функций, выражающихся через элементарные. Ограничиваясь конечным числом членов разложения получаем приближенное решение. Примером может служить метод частотных характеристик, широко применяемый в теории автоматического управления. Однако эти методы удобны лишь в том случае, когда большую часть промежуточных выкладок удается сделать точно. Это выполнимо для сравнительно простых задач и сильно сужает область применения приближенных методов. Численные методы - это алгоритмы вычисления приближенных значений искомого решения на некоторой выбранной сетке значений аргумента х. Численные методы не позволяют найти общего решения, но могут дать частное решение для очень широкого класса уравнений и задач. Поэтому с появлением быстродействующих ЭВМ численные методы стали одним из основных способов решения дифференциальных уравнений для практических задач. Самым простым способом решения численного решения первого порядка является метод Эйлера (ломаных, трапеций), который заключается в следующем. Выразим производную в явном виде, как некую функцию от х и у.
Затем заменим производную отношением конечных разностей (приращений).
При известных начальных условиях получаем:
задаваясь приращением по х получим выражение для следующей точки интегральной кривой
и так далее. Соединяя отрезками полученные точки получим ломаную - приближенное изображение частного решения исходного дифферен-циального уравнения. Эта ломаная называется ломаной Эйлера. Недостатком этого метода является его низкая точность, обусловленная накоплением ошибки на каждом шаге, поскольку отношение конечных разностей не равно в точности производной. Поэтому добиться удовлетворительной точности метода можно лишь при очень малом шаге по х. Порядок точности можно повысить путем усложнения разностной схемы. Идея метода Рунге заключается в расчете по схеме Эйлера по двум сеткам имеющим общие узлы с шагами h1, h2 (h2=h1/2) и ввести корректирующий параметр s, повышающий точность решения. Дальнейшее развитие идей повышения точности произошло в методах Рунге-Кутта, среди которых наибольшее распространение получил метод четвертого порядка, реализуемый по следующим формулам (для системы диф. уравнений) :
Для одного диф. уравнения эти формулы также применимы, в них надо лишь опустить индекс j.
12 |




 (5.1)
(5.1) . (5.2)
. (5.2)

 в ряд вблизи точки
в ряд вблизи точки  и ограничимся первыми двумя членами разложения
и ограничимся первыми двумя членами разложения  . Учтя уравнение (1) и обозначив
. Учтя уравнение (1) и обозначив  , получаем
, получаем  Эту формулу можно применять многократно, находя значения функции во все новых и новых точках.
Эту формулу можно применять многократно, находя значения функции во все новых и новых точках. (5.3)
(5.3)
 и использовать его для аппроксимации решения на всем интервале
и использовать его для аппроксимации решения на всем интервале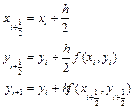




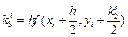




 , откуда
, откуда .
. , откуда,
, откуда,
