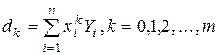 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Интерполяционная формула Лагранжа 12
Пусть на отрезке [a, b] даны n + 1 различных значений аргумента: x, x, ..., xn и известны для функции y = f (х) соответствующие значения выражений
Требуется построить полином Ln(x) степени не выше n, имеющий в заданных узлах x, x, ..., xn те же значения, что и функция f (х), т. е. тaкой, что Ln(xi) = yi (i = 0, 1, ..., n) Будем искать Ln(x) в виде:
где li(x) - полином степени n, причем
Очевидно, что требование (3.7) с учетом (3.6) обеспечивает выполнение условий (3.3) (Рисунок 3.2).
Рисунок 3.2. li (x) - полином степени n
Так как искомый полином li(x) обращaется в нуль в n точках x,…, xi - , xi + , ..., xn, то он имеет вид
где Сi - постоянный коэффициент. Полагая в формуле (8) х = xi и учитывая, что li(xi) = yi, получим: yi = Ci (xi - x)(xi - x) ... (xi - xi -)(xi - xi +) ... (xi - xn). Отсюда Сi = Заметим, что ни один из множителей не равен нулю. Подставляя Сi a (3.8), а также с учетом (3.6), окончательно имеем:
Это и есть интерполяционная формула Лагранжа. Если функция у(х) известна только в некоторых точках xi (называемых узлами сетки) и задана некоторой таблицей, то очень часто возникает необходимость знать значение этой функции в некоторых промежуточных точках. Для этого подбирают некоторую функцию j(х), которая по некоторому критерию близка к у(х) и относительно просто вычисляется. Наиболее просто потребовать, чтобы j(х) совпадала с табличными значениями в n выбранных узлах сетки. Поскольку функция j(х) зависит также от неизвестных параметров аi, то правильнее её рассматривать в виде j(x,ai). В этом случае нахождение функции j(x,ai) сводится к решению системы уравнений: j(xi,a1,a2,...,an)=y(xi) Если j(x,ai) нелинейно зависит от параметров, то интерполяцию называют нелинейной и в общем случае нахождение параметров из решения системы уравнений может быть трудной задачей. Если j(x,ai) линейно зависит от параметров, то интерполяция называется линейной, а функция j(x,ai) может быть представлена в виде так называемого обобщенного многочлена:
jk(x) - линейно-независимые функции, поскольку в противном случае число слагаемых можно было бы уменьшить. Таким образом, определение параметров ak может быть осуществлено из решения системы линейных уравнений:
Чтобы задача интерполяции имела единственное решение, необходимо, чтобы определитель системы уравнений был отличен от нуля. Система функций, удовлетворяющих этому требованию называется чебышевской.
Наиболее простой системой функций, удовлетворяющей вышеназванным требованиям является интерполяционный многочлен Лагранжа. В этом случае используется многочлен n-ой степени вида: P(x)=C0(x-x1)(x-x2)...(x-xn)+C1(x-x0)(x-x2)...(x-xn)+C2(x-x0)(x-x1)(x-x3)...(x-xn)+... ...+Cn(x-x0)(x-x1)...(x-xn-1). Коэффициенты C0,C1,...,Cn определяются из выполнения условий P(x0)=y0, P(x1)=y1, ...,P(xn)=yn. Подставив вместо x его значения xi получим следующие выражения для коэффициентов С:
............................................................
Подставив полученные значения С в исходную формулу получим интерполяционную формулу Лагранжа:
Другим видом интерполяционного многочлена является полином Ньютона. Этот полином строится с помощью так называемых разделенных разностей различных порядков, находимых по значениям функции в точках сетки. По определению разделенные разности первого порядка находятся так:
Разделенные разности второго порядка определяются с помощью разностей первого порядка:
И, соответственно, разности n-ого порядка вычисляются по формуле:
Построение интерполяционного полинома Ньютона очень просто и основывается на следующем. Пусть х - произвольная точка отрезка [a,b]. Рассмотрим разделенную разность первого порядка:
Из этого выражения можно выразить значение f(x)=y1+(x-x1)f(x,x1). Поскольку разность второго порядка имеет вид:
Откуда можно выразить разделенную разность первого порядка f(x,x1)=f(x1,x2)+f(x,x1,x2)(x-x2). Когда необходимо провести график функции по известным точкам y(xi), то проще всего воспользоваться лекалом. Однако, если токи расположены редко или несколько разбросано, то нелегко подобрать участок лекала, проходящий сразу через несколько точек. Тогда можно взять гибкое лекало - металлическую линейку, поставить её на ребро и зафиксировав пальцами в известных точках изогнуть так, чтобы ребро линейки проходило через все точки. Этот способ интерполяции можно описать математически. Он называется интерполяцией с помощью сплайн-функций. Сплайн (splain) в переводе с английского как раз и означает «гибкая линейка». При этом сплайн-функцию можно наглядно трактовать как линию, которую образовала бы гибкая линейка, будучи закрепленной в ряде точек - узлов интерполяции. Математически же сплайн - специальный многочлен, принимающий в узлах интерполяции значения y(x)=yi=y(xi) и обеспечивающий непрерывность производных в этих точках. Для определения вида сплайн- функции пользуются известным из курса сопротивления материалов уравнением равновесия гибкого упругого бруска jIV(x)=0. Откуда следует, что в промежутке между парой соседних узлов интерполяционная функция является многочленом третьей степени, который удобно записать в следующем виде: j(x)=ai+bi(x-xi-1)+ci(x=xi-1)2+di(x-xi-1)3, xi-1 £x £xi. Коэффициенты многочлена на каждом интервале определяют из условия равенства многочлена значениям функции в узлах интерполяции: yi-1=j(xi-1)=ai, 1£ i £ N yi=j(xi)=ai+bihi+cihi2+dihi3, где hi=xi-xi-1 Число этих уравнений меньше числа неизвестных коэффициентов, поэтому для определенности системы нужны дополнительные условия. Для их получения вычислим первую и вторую производные многочлена j(х) и наложим условие их непрерывности (т.е. гладкости линейки) во всех его точках, включая узлы. j’(x)=bi+2ci(x-xi-1)+3di(x-xi-1)2, j’’=2ci+6di(x-xi-1) при хi-1 £ x £ xi Приравнивая правые и левые производные в узле xi получим дополнительные уравнения: bi+1=bi+2cihi+3dihi2, 1£ i £ N-1 ci+1=ci+3dihi , 1£ i £ N-1 Недостающие два уравнения получают из предположения о нулевой кривизне графика на концах рассматриваемого участка: 1/2j’’(x0)=c1=0, 1/2j’’(xn)=cn+3dnhn=0. Но если есть иные дополнительные сведения о поведении функции на границах интервала, то можно записать другие краевые уравнения. Таким образом, мы получили систему для определения 4N неизвестных коэффициентов. Эта система может быть решена рассмотренными ранее способами решения систем уравнений. В более широком смысле задача интерполяции функции сплайном эквивалентна задаче определения многочлена n-ой степени:
коэффициенты которого кусочно- постоянны и который в узлах интерполяции принимает заданные значения и непрерывен вместе со своими n-1 производными. При нечетной степени многочлена n=2p-1 сплайн- интерполяцию можно рассматривать как решение задачи Лагранжевой интерполяции при дополнительном условии:
Из этого условия как раз и следует S(2p)(x)=0 для интерполирующей функции, условия непрерывности (2p-2) производных во внутренних узлах и естественные ограничения на производные в крайних узлах. Хотя сплайн- интерполяция осуществима при переменном шаге, но значительное изменение шага нецелесообразно, поскольку при этом теряются её преимущества и существенно возрастает погрешность. С применением сплайн -интерполяции также возможно численное интегрирование , спектральный анализ и другие математические операции. На практике наиболее часто используются два случая. Один - подробно рассмотренный случай с n=3, второй - n=1, когда сплайн соответствует аппроксимации графика ломаной (определение коэффициентов при этом очевидно). Таким образом, для каждого отрезка [xi,xi+1] кубическая сплайн - функция может быть записана в виде:
hi=xi+1-xi ,fi(x)=y(x), mi=f’’(xi) и i=1,2,...,n (n- количество узлов). При проведении интерполяции необходимо вначале определить между какими двумя известными узлами расположена интересующая нас точка, затем подставить соответствующие значения и подсчитать сплайн- функцию. При проведении экстраполяции интересующая нас точка находится вне интервала и для отыскания значения функции в ней предполагается, что наклон линейного участка f(x) равен первой производной сплайн -функции в точке (x1,y1) для x<x1 или в точке (xn,yn) при x>xn. Пусть в результате измерений в процессе опыта получено табличное задание некоторой функции f(х), выражающей связь между двумя географическими параметрами: Таблица 3.1.
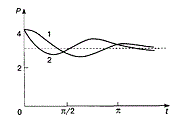
Конечно, можно найти формулу, выражающую эту зависимость аналитически, применив метод интерполяции. Однако, совпадение значений полученного аналитического задания функции в узлах интерполяции с имеющимися эмпирическими данными часто может вовсе не означать совпадение характеров поведения исходной и интерполирующей функции на всем интервале наблюдения. Кроме того, табличная зависимость географических показателей всегда получается в результате измерений различными приборами, имеющими определенную и не всегда достаточно малую погрешность измерения. Требование точного совпадения значений приближающей и приближаемой функций в узлах является тем более неоправданным, если значения функции f(х), полученные в результате измерений уже сами являются приближенными. Задача аппроксимации функции одной переменной с самого начала обязательно учитывает характер поведения исходной функции на всем интервале наблюдений. Формулировка задачи выглядит следующим образом. Функция у= f(х) задана таблицей (3.1). Необходимо найти функцию заданного вида: y=F(x) (3.10) которая в точках x1, x2, …, xn принимает значения, как можно более близкие к табличным y1, y2, …, yn. На практике вид приближающей функции чаще всего определяют путем сравнения вида приближенно построенного графика функции у= f(х) с графиками известных исследователю функций, заданных аналитически (чаще всего простых по виду элементарных функций). А именно, по таблице (1) строится точечный график f(x), затем проводится плавная кривая, по возможности наилучшим образом отражающая характер расположения точек. По полученной таким образом кривой на качественном уровне устанавливается вид приближающей функции. Рассмотрим рисунок 4.1.
Рисунок 3.3 На рисунке изображены три ситуации: На графике (а) взаимосвязь х и у близка к линейной; прямая линия здесь близка к точкам наблюдений, и последние отклоняются от нее лишь в результате сравнительно небольших случайных воздействий. На графике (b) реальная взаимосвязь величин х и у описывается нелинейной функцией, и какую бы мы ни провели прямую линию, отклонение точек наблюдения от нее будет существенным и неслучайным. В то же время, проведенная ветка параболы достаточно хорошо отражает характер зависимости между величинами. На графике (с) явная взаимосвязь между переменными х и у отсутствует; какую бы мы ни выбрали формулу связи, результаты ее параметризации будут здесь неудачными. В частности, обе выбранные прямые одинаково плохи для того, чтобы делать выводы об ожидаемых значениях переменной у по значениям переменной х. Следует заметить, что строгая функциональная зависимость для таблицы исходных данных наблюдается редко, ибо каждая из участвующих в ней величин может зависеть от многих случайных факторов. Однако формула (3.10) (ее называют эмпирической формулой или уравнением регрессии у на х) интересна тем, что позволяет находить значения функции f для нетабличных значений х, "сглаживая" результаты измерений величины у, т.е. на всем интервале изменения х. Оправданность такого подхода определяется в конечном счете практической полезностью полученной формулы. Через имеющееся "облако" точек всегда можно попытаться провести линию установленного вида, которая является наилучшей в определенном смысле среди всех линий данного вида, то есть "ближайшей" к точкам наблюдений по их совокупности. Для этого определим вначале понятие близости линии к некоторому множеству точек на плоскости. Меры такой близости могут быть различными. Однако, любая разумная мера должна быть, очевидно, связана с расстоянием от точек наблюдения до рассматриваемой линии (задаваемой уравнением y=F(x)). Предположим, что приближающая функция F(x) в точках х1, x2, ..., xn имеет значения y1, y2, ..., yn. Часто в качестве критерия близости используется минимум суммы квадратов разностей наблюдений зависимой переменной yi и теоретических, рассчитанных по уравнению регрессии значений yi. Здесь считается, что yi и xi - известные данные наблюдений, а F - уравнение линии регрессии с неизвестными параметрами (формулы для их вычисления будут приведены ниже). Метод оценивания параметров приближающей функции, минимизирующий сумму квадратов отклонений наблюдений зависимой переменной от значений искомой функции, называется методом наименьших квадратов (МНК) или Least Squares Method (LS). Итак, задачу приближения функции f теперь можно сформулировать следующим образом: для функции f, заданной таблицей (1), найти функцию F определенного вида так, чтобы сумма квадратов Ф была наименьшей.
Рассмотрим метод нахождения приближающей функции в общем виде на примере аппроксимирующей функции с тремя параметрами:
Пусть F(xi, a, b, c) = yi, i=1, 2, ..., n. Сумма квадратов разностей соответствующих значений f и F будет иметь вид:
Эта сумма является функцией Ф(а, b, c) трех переменных (параметров a, b и c). Задача сводится к отысканию ее минимума. Используем необходимое условие экстремума:
Получаем систему для определения неизвестных параметров a, b, c. Данная система называется нормальной системой уравнений метода наименьших квадратов.
Решив эту систему трех уравнений с тремя неизвестными относительно параметров a, b, c, мы и получим конкретный вид искомой функции F(x, a, b, c). Как видно из рассмотренного примера, изменение количества параметров не приведет к искажению сущности самого подхода, а выразится лишь в изменении количества уравнений в системе (3.13). Естественно ожидать, что значения найденной функции F(x, a, b, c) в точках х1, x2, ..., xn, будут отличаться от табличных значений y1, y2, ..., yn. Значения разностей yi-F(xi,a, b, c)=e i (i=1, 2, ..., n) называются отклонениями измеренных значений y от вычисленных по формуле (3.10). Для найденной эмпирической формулы (3.10) в соответствии с исходной таблицей (3.1) можно, следовательно найти сумму квадратов отклонений
которая в соответствии с методом наименьших квадратов для заданного вида приближающей функции (и найденных значений параметров) должна быть наименьшей. Из двух разных приближений одной и той же табличной функции, следуя методу наименьших квадратов, лучшим нужно считать то, для которого сумма (3.12) имеет наименьшее значение. В экспериментальной практике в качестве приближающих функций в зависимости от характера точечного графика f часто используются приближающие функции с двумя параметрами:
Очевидно, что когда вид приближающей функции установлен, задача сводится только к отысканию значений параметров. Рассмотрим наиболее часто встречающиеся в практических исследованиях эмпирические зависимости. 1. Линейная функция (линейная регрессия). Начальным пунктом анализа зависимостей обычно является оценка линейной зависимости переменных. Следует при этом учитывать, однако, что "наилучшая" по методу наименьших квадратов прямая линия всегда существует, но даже наилучшая не всегда является достаточно хорошей. Если в действительности зависимость y=f(x) является квадратичной, то ее не сможет адекватно описать никакая линейная функция, хотя среди всех таких функций обязательно найдется "наилучшая". Если величины х и у вообще не связаны, мы также всегда сможем найти "наилучшую" линейную функцию y=ax+b для данной совокупности наблюдений, но в этом случае конкретные значения а и b определяются только случайными отклонениями переменных и сами будут очень сильно меняться для различных выборок из одной и той же генеральной совокупности. Рассмотрим теперь задачу оценки коэффициентов линейной регрессии более формально. Предположим, что связь между x и y линейна и искомую приближающую функцию будем искать в виде:
Найдем частные производные по параметрам: Подставим полученные соотношения в систему вида ( 3.15 ):
Далее имеем:
или, деля каждое уравнение на n:
Введем обозначения:
Тогда последняя система будет иметь вид:
Коэффициенты этой системы Mx , My , Mxy , Mx2 - числа, которые в каждой конкретной задаче приближения могут быть легко вычислены по формулам ( 4.7 ), где xi, yi - значения из таблицы (3.1). Решив систему (3.13), получим значения параметров a и b , а следовательно, и конкретный вид линейной функции .
2. Квадратичная функция (квадратичная регрессия). Будем искать приближающую функцию в виде квадратного трехчлена:
Находим частные производные:
Составим систему вида (5):
После несложных преобразований получается система трех линейных уравнений с тремя неизвестными a, b, c. Коэффициенты системы, так же как и в случае линейной функции, выражаются только через известные данные из таблицы (4.1):
Здесь использованы обозначения (3.16), а также
Решение системы (3.19) дает значение параметров a, b и с для приближающей функции (3.18). Квадратичная регрессия применяется, если все выражения вида у2 -2y1 + y0 , y3 -2 y2 + y1 , y4 -2 y3 + y2 и т.д. мало отличаются друг от друга. Линейный парный регрессионный анализ заключается а определении параметров эмпирической линейной зависимости y(x)=b1x+b0 описывающим связь между некоторым числом n пар значений xi и yi, обеспечивающим при этом наименьшую среднеквадратичную погрешность. Графически эту задачу можно представить следующим образом - в облаке точек на плоскости XOY требуется провести прямую так, чтобы величина всех отклонений отвечала условию:
где y(xi) - эмпирическая зависимость с неизвестными параметрами. Для нахождения неизвестных параметров в соответствии со свойствами экстремума необходимо приравнять нулю частные производные от целевой функции по неизвестным параметрам.
что и дает систему линейных уравнений для определения неизвестных коэффициентов.
Выражая решение системы в явном виде получим:
Нелинейная парная регрессия сводится к получению заданной нелинейной зависимости (в большинстве случаев линейной по параметрам), приближающей совокупность точек с наименьшей среднеквадратичной погрешностью. Для упрощения расчетов производится сведение нелинейной регрессии к линейной с помощью линеаризующих преобразований. Хотя в общем случае гораздо удобнее использовать специальные программы нелинейных регрессий. Примеры линеаризующих преобразований приведены в следующей таблице.
Гиперболическая регрессия заключается в нахождении параметров функции y(x)=b0+b1/x из решения системы уравнений:
Степенная регрессия обеспечивает нахождение параметров функции y(x)=b0xb1. Это производится по формулам:
Показательная регрессия обеспечивает получение параметров a и b показательной функции y(x)=abx из решения системы уравнений.
Экспоненциальная регрессия обеспечивает получение параметров функции y(x)=b0exp(b1x) по формулам:
Логарифмическая регрессия дает параметры a и b функции y=a+blgx из решения системы уравнений:
Параболическая регрессия обеспечивает получение трех параметров b0,b1 и b2 приближения параболической функцией y(x)=b0+b1x+b2x2 из решения системы трех уравнений.
Полиномиальная аппроксимация обеспечивает нахождение коэффициентов полинома y(x)=a0+a1x+a2x2+...+amxm из решения системы уравнений:
где
Полином степени m<n, где n - число пар точек, обеспечивает аппроксимацию с определенной погрешностью в узлах интерполяции. При m=n значения полинома точно совпадают с Yi. Для решения систем уравнений можно использовать ранее рассмотренные программы из лабораторной работы №1.
12 |
.
, где
, 1£ i £ n.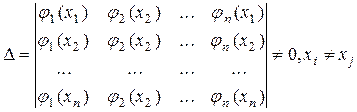
Практика показала, что аппроксимация с помощью интерполяционного полинома Лагранжа является достаточно эффективной, когда интерполируются гладкие функции и число точек является малым. Более того, в математическом обеспечении ЭВМ для сглаживания данных часто используется формула Лагранжа при N=4. При большем числе точек пользоваться Формулой Лагранжа становится не очень удобно.
,
, где
(3.11)
(3.12)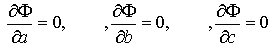
(3.13)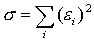
,
(3.14)
(3.16)
(3.17)
(3.18)
(3.19)
,
,
.
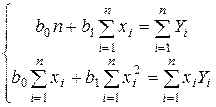
