 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Обробка результатів вимірювання.
Лабораторна робота № 6 Визначення коефіцієнта лінійного розширення твердих тіл. Мета роботи – визначити коефіцієнт лінійного розширення твердих тіл. Прилади і обладнання: прилад для визначення коефіцієнта лінійного розширення твердих тіл (ПРТТ); стержні: стальний, латунний, алюмінієвий, металева пробірка, термометр.
Теоретичні відомості. Тепловий рух частинок твердого тіла, як конденсованого середовища, суттєво відрізняється від теплового руху в газі. Структурні частинки, з яких складається кристал ( атоми, молекули або іони), зв’язані між собою силами взаємодії, що залежать від відстаней, здійснюють коливання навколо положень рівноваги, які збігаються з вузлами кристалічної гратки. У речовин в твердому стані енергія теплового руху Щоб пояснити теплове розширення твердих тіл, розглянемо криву залежності потенціальної енергії взаємодії частинок від відстані між ними ( рис. 6.1).
Рис. 6.1. Для порівняння на цьому рисунку пунктирною лінією зображена залежність від відстані результуючої сили взаємодії частинок. Якщо частинка крім потенціальної енергії має ще й деяку кінетичну енергію
Рис. 6.2. Отже, з ростом температури зростає середня відстань між частинками тіла і його об’єм збільшується. Якщо б частинки твердого тіла виконували гармонічні коливання, або, іншими словами, коли б крива енергії була симетричною, то тверді тіла б не розширялись при нагріванні. При нагріванні тіла з початковою довжиною
де Коефіцієнт лінійного розширення чісельно рівений відносному видовженню тіла при нагріванні його на один градус і виражається формулою
де Користуватись формулою (6.1) для визначення
де Довжина тіла при будь – якій температурі може бути виражена через його довжину при 0 0С. Із формули (6.1) випливає, що
де
З цієї формули випливає фізичний зміст В результаті розширення збільшується і об’єм тіла. Розглянемо тіло у вигляді куба з ребром
Піднесемо
де
Для твердих тіл Для анізотропних кристалів коефіцієнт лінійного розширення
Опис приладу. У цій роботі необхідно визначити середній коефіцієнт лінійного розширення трьох стержневих зразків: стального, алюмінієвого і латунного в інтервалі температур від кімнатної Прилад для визначення коефіцієнта лінійного розширення металів ( рис. 6.3) складається із корпуса 1, до якого кріпиться захисний корпус – кожух 2. Всередині кожуха 2 встановлений нагрівник. При проведенні дослідів у нагрівник через прокладку 3 вставляють металеву пробірку 4 зі стержнем. На корпусі приладу встановлений стояк з кронштейном для індикатора малих переміщень 5. На панелі корпуса розташовані лампа 6 і кнопковий вимикач 7. Штепсельна вилка служить для вмикання приладу в електричну мережу напругою 220 В.
Рис. 6.3.
Порядок виконання роботи. 1. Виміряти штангенциркулем лінійні розміри трьох стержнів із різних металів. 2. Пробірку на 0,5 об’єму наповнити водою з крана і виміряти термометром її температуру 3. Опустити в пробірку один із зразків і ввести пробірку в нагрівач. 4. Встановити індикатор над пробіркою і опустити шток вимірювача в заглибину на торці стержня. Установити стрілку індикатора на нульову позначку. 5. Увімкнути живлення приладу. 6. При закипанні води в пробірці досліджуваний стержень набуває температури кипіння води 7. Довжину стержня 8. Температуру кипіння 9. Для проведення дослідів з іншими зразками необхідно: а) вимкнути живлення приладу; б) вийняти із приладу нагріту металеву пробірку із стержнем; в) витягнути стержень і вилити гарячу воду; г) охолодити пробірку водою з крана. 10. Повторити пп. 2 – 8 з другим, а потім з третім стержнем. 11. Дані вимірювань, обрахунків і табличні дані для
Обробка результатів вимірювання. 1. За формулою (6.2) розрахувати середній коефіцієнт лінійного розширення стержнів, виготовлених із різних матеріалів.
=
=
=
2. Точність вимірювання
Висновки: В результаті проведених експериментів було визначено коефіцієнти лінійного розширення твердих тіл:
- стального стержня a =
- латунного стержня a =
- алюмінієвого стержня a = |



 набагато менша, ніж потенціальна енергія взаємодії частинок між собою. З підвищенням температури зростає енергія теплових коливань частинок, а також відбувається теплове розширення – збільшення об’єму тіла.
набагато менша, ніж потенціальна енергія взаємодії частинок між собою. З підвищенням температури зростає енергія теплових коливань частинок, а також відбувається теплове розширення – збільшення об’єму тіла.
 , яка відповідає температурі
, яка відповідає температурі  , то вона перебуватиме не в точці
, то вона перебуватиме не в точці  , а дещо вище – в точці
, а дещо вище – в точці  на рівні
на рівні  . Точки перетину прямої
. Точки перетину прямої  з кривою енергії визначають крайні положення, які займає частинка при коливаннях. Причому в положенні
з кривою енергії визначають крайні положення, які займає частинка при коливаннях. Причому в положенні  кінетична енергія частинки дорівнює потенціальній енергії відштовхування, а в положенні
кінетична енергія частинки дорівнює потенціальній енергії відштовхування, а в положенні  - потенціальній енергії притягання. Внаслідок різної залежності сил притягання і відштовхування між частинками від відстані між ними крива потенціальної енергії несиметрична. Тому при русі вправо частинка зміщується на більшу відстань, ніж при русі вліво і, отже, коливання частинки є ангармонічними. Очевидно, що положення рівноваги частинки при даній температурі відповідає середині відрізка
- потенціальній енергії притягання. Внаслідок різної залежності сил притягання і відштовхування між частинками від відстані між ними крива потенціальної енергії несиметрична. Тому при русі вправо частинка зміщується на більшу відстань, ніж при русі вліво і, отже, коливання частинки є ангармонічними. Очевидно, що положення рівноваги частинки при даній температурі відповідає середині відрізка  ( лінія, що відповідає середнім положенням частинки, зображена на рис. 6.2 пунктиром).
( лінія, що відповідає середнім положенням частинки, зображена на рис. 6.2 пунктиром).
 його відносне видовження
його відносне видовження  пропорційне зміні температури тіла
пропорційне зміні температури тіла  :
: ,
, - приріст довжини тіла;
- приріст довжини тіла;  - коефіцієнт пропорційності, який називається істинним коефіцієнтом лінійного розширення
- коефіцієнт пропорційності, який називається істинним коефіцієнтом лінійного розширення 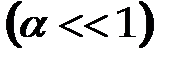 .
.  , (6.1)
, (6.1) - довжина тіла при 0 0С;
- довжина тіла при 0 0С;  - довжина тіла при
- довжина тіла при  0С;
0С;  .
. і
і  при температурах відповідно
при температурах відповідно 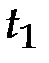 і
і  за допомогою (6.5) виводять таку робочу формулу для визначення
за допомогою (6.5) виводять таку робочу формулу для визначення  :
: , (6.2)
, (6.2) . Визначений за формулою (6.2) коефіцієнт слід вважати середнім, оскільки
. Визначений за формулою (6.2) коефіцієнт слід вважати середнім, оскільки  .
. , (6.3)
, (6.3) , оскільки
, оскільки  = 0 0С. Разом з тим формулу (6.1) можна представити у вигляді
= 0 0С. Разом з тим формулу (6.1) можна представити у вигляді .
. стержня довжиною
стержня довжиною  .Початковий його об’єм при 0 0С буде
.Початковий його об’єм при 0 0С буде  . Очевидно, при температурі
. Очевидно, при температурі  об’єм тіла буде дорівнювати
об’єм тіла буде дорівнювати .
. до кубу і нехтуючи членами, які містять
до кубу і нехтуючи членами, які містять  і
і  , скільки вони мають малі значення, одержимо
, скільки вони мають малі значення, одержимо ,
, - середній коефіцієнт об’ємного розширення. Істинний коефіцієнт об’ємного розширення дорівнює
- середній коефіцієнт об’ємного розширення. Істинний коефіцієнт об’ємного розширення дорівнює .
. - величина порядку 10-5 К-1, а для газів – 10-3 К-1.
- величина порядку 10-5 К-1, а для газів – 10-3 К-1. до температури кипіння води
до температури кипіння води  .
.
 , де
, де  - ціна однієї поділки;
- ціна однієї поділки;  - кількість поділок, на які відхилилась стрілка індикатора від нульової позначки.
- кількість поділок, на які відхилилась стрілка індикатора від нульової позначки. .
. , мм
, мм , мм
, мм , мм
, мм , К-1
, К-1 , К-1
, К-1











 =
= 
 =
= 
 =
= 