 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Исследование переходных процессов в электрических цепях
по дисциплине «Электротехника»
Выполнил студент 2 курса группы 11-ББ-ИБ-3 Благочиннов Е.Д. Проверил: профессор Тельнов Г.В.
Краснодар Цель работы: 1. Исследование переходных процессов в линейных электрических цепях при наличии одного или двух накопителей энергии. 2. Определить влияние параметров исследуемой цепи на характер переходного процесса. 3. Привить навыки проведения научных исследований и использования электронного осциллографа для исследования быстропротекающих периодических процессов.
Учебные вопросы: 1. Исследование переходного процесса в RC цепях. 2. Исследование переходного процесса в RL цепях. 3. Исследование переходного процесса в последовательной RLС цепи.
1 Исследование переходного процесса в RC цепях
Составим электрическую схему для исследования переходных процессов в RC цепи и подключим её к источнику постоянного напряжения через коммутационный элемент, как показано на рисунке 1.1.
Рис 1.1 Схема для исследования переходного процесса в RC цепи Пронаблюдаем на экране осциллографа, представленного на рисунке 1.2, переходный процесс в исследуемой цепи до полной развёртки, осуществляя при этом коммутацию ключа (размыкание и замыкание). При замкнутом ключе конденсатор заряжен, значит, при размыкании ключа конденсатор начнёт разряжаться, а так как мгновенно конденсатор разрядиться не может, то возникнет переходный процесс, связанный с разрядкой конденсатора. Если при полной разрядке конденсатора замкнуть ключ, то возникнет переходный процесс, связанный с зарядкой конденсатора. Для измерения длительности переходного процесса установим курсор «1» в начало изменения сигнала на входе, что соответствует максимальному значению напряжения на конденсаторе. Курсор «2» установим в положение соответствующее 5% от максимального напряжения на конденсаторе. Снимем значение, соответствующее времени окончания переходного процесса (3

  Рис 1.2 Осциллограмма переходного процесса в RC цепи Как видно из осциллограммы измеренное время окончания переходного процесса практически равно расчётному:
На графическом дисплее (Display Graph), представленном на рисунке 1.3, показаны графические зависимости переходного процесса.

 
    Рис 1.3 Графические зависимости переходного процесса в RC цепи
Зная, что постоянная времени равна
Для измерения постоянной времени подведём курсор «1» в начало изменения сигнала на входе, что соответствует максимальному значению напряжения на конденсаторе, а курсор «2» к точке где напряжение на конденсаторе падает в e раз (
Измерив разность во времени между положениями курсоров получим значение приблизительно равное теоретическому:
Проведём аналогичные исследования для различных параметров RC цепей и результаты занесём в таблицу 1.1. Так как входное параметры источника постоянного напряжения не меняются, то вычислим значения напряжений для установки курсоров (при условии, что конденсатор заряжается и разряжается полностью):
Таблица 1.1
Исходя из таблицы видно, что постоянная времени в RC цепях линейно зависит от ёмкости конденсатора и от сопротивления резистора, причём зависимость – прямо пропорциональная. Так как время переходного процесса есть троекратное значение постоянной времени, то оно так же линейно и прямо пропорционально зависит от сопротивления и ёмкости. Чем больше ёмкость и сопротивление, тем больше постоянная времени и, соответственно, время переходного процесса и наоборот.
2 Исследование переходного процесса в RL цепях
Составим электрическую схему для исследования переходных процессов в RL цепи и подключим её к источнику постоянного напряжения через коммутационный элемент, как показано на рисунке 2.1.
Рис 2.1 Схема для исследования переходного процесса в RL цепи Пронаблюдаем на экране осциллографа, представленного на рисунке 2.2, переходный процесс в исследуемой цепи до полной развёртки, осуществляя при этом коммутацию ключа (размыкание и замыкание). При замкнутом ключе катушка индуктивности подключена к источнику постоянного напряжения, а при размыкании ключа возникает переходный процесс.
Для измерения длительности переходного процесса установим курсор «1» в начало изменения сигнала на входе, что соответствует максимальному значению отклонения напряжения от нулевого значения. Курсор «2» установим в положение соответствующее 5% от максимального значения отклонения от нулевого значения напряжения на катушке. Снимем значение, соответствующее времени окончания переходного процесса (3
 
  Рис 2.2 Осциллограмма переходного процесса в RL цепи Как видно из осциллограммы измеренное время окончания переходного процесса практически равно расчётному:
На графическом дисплее (Display Graph), представленном на рисунке 1.3, показаны графические зависимости переходного процесса.
 

 Рис 2.3 Графические зависимости переходного процесса в RL цепи Зная, что постоянная времени равна
Для измерения постоянной времени подведём курсор «1» в начало изменения сигнала на входе, что соответствует максимальному значению напряжения на конденсаторе, а курсор «2» к точке где напряжение на конденсаторе падает в e раз (
Измерив разность во времени между положениями курсоров получим значение приблизительно равное теоретическому:
Проведём аналогичные исследования для различных параметров RL цепей и результаты занесём в таблицу 2.1.
Таблица 2.1
Исходя из таблицы видно, что время переходного процесса в RL цепях зависимость напряжения на катушке от её индуктивности прямо пропорциональна, а зависимость от сопротивления резистора обратно пропорциональна. Значит чем больше индуктивность и меньше сопротивление тем больше длительность переходного процесса в RL цепи.
2 Исследование переходного процесса в последовательной RLC цепи
Составим электрическую схему для исследования переходных процессов в RLC цепи и подключим её к источнику постоянного напряжения через коммутационный элемент, как показано на рисунке 3.1.
Рис 3.1 Схема для исследования переходного процесса в RLC цепи
Пронаблюдаем на экране осциллографа, представленного на рисунке 3.2, переходный процесс в исследуемой цепи до полной развёртки, осуществляя при этом коммутацию ключа (размыкание и замыкание). При замыкании ключа ёмкостной элемент заряжается от источника постоянного напряжения, а при размыкании ключа конденсатор разряжается и его энергия электрического поля переходит в энергию магнитного поля катушки и частично рассеивается на резистивном элементе. Возникает переходный процесс.
При помощи осциллограммы, показанной на рисунке 3.3, измерим период колебаний колебательного процесса разрядки и зарядки.
   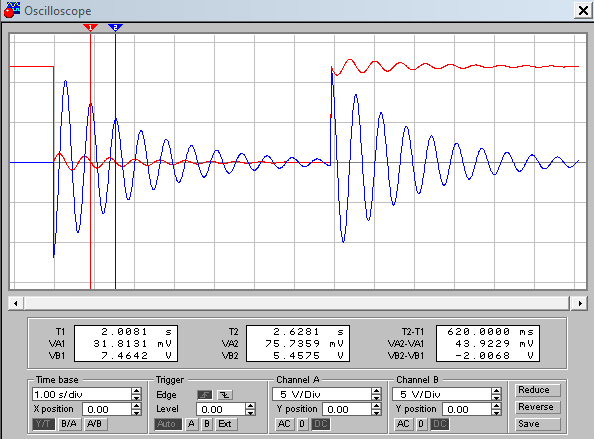 Рис 3.2 Осциллограмма переходного процесса в RLС цепи Из показаний осциллограммы снимем период колебаний:
Учитывая настройки потенциометра, рассчитаем коэффициент затухания (α) по формуле:
На графическом дисплее (Display Graph), представленном на рисунке 3.3, показаны графические зависимости переходного процесса.
   Рис 3.3 Графические зависимости переходного процесса в RLС цепи
Как видно из графических зависимостей процесс разрядки ёмкостного элемента в исследуемой RLC цепи имеет колебательный характер, значит для корней характеристического уравнения справедливо неравенство:
Найдём сопротивление, при котором процесс разрядки ёмкостного элемента в имеет апериодический характер для этого решим неравенство:
Проведём аналогичные исследования для различных параметров RL цепей и результаты занесём в таблицу 3.1.
Таблица 3.1
Из таблицы видно, что коэффициент затухания прямо пропорционально зависит от сопротивления и обратно пропорционально от ёмкости.
Вывод
|




 ). Рассчитаем теоретическое время окончания переходного процесса по следующей формуле, зная, что постоянная времени
). Рассчитаем теоретическое время окончания переходного процесса по следующей формуле, зная, что постоянная времени  :
: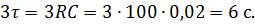







 ) и замерим разницу во времени:
) и замерим разницу во времени:



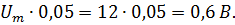



 :
:




















