 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Приближенное решение уравнений
Лабораторная работа 4 РЕШЕНИЕ НЕЛИНЕЙНЫХ УРАВНЕНИЙ И СИСТЕМ НЕЛИНЕЙНЫХ УРАВНЕНИЙ. РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ Цель работы: - изучить встроенные функции root(), polyroots(), Given-Find(); - найти корни нелинейных уравнений с одной переменной; - найти корни полинома; - решить систему нелинейных уравнений; - решить систему линейных уравнений
Задание 1. Решить одно уравнения с одним неизвестным с точностью до 0,0001. Выполнить проверку решения.
Рассмотрим одно алгебраическое уравнение с одним неизвестным х f(x)=0. Для решения таких уравнений в Mathcad’e имеется встроенная функция root( ), которая имеет два формата: - root(f(х),х); - root(f(х),х,а,b); Здесь: - f (х) - скалярная функция с одним неизвестным, - х- скалярная переменная, относительно которой решается уравнение, - а, b - границы интервала, внутри которого происходит поиск корня. Первый формат функции root( ) требует дополнительного задания начального значения (guess value) переменной х, вблизи которой будет производиться поиск корня. Приведем пример решения уравнения 2·sin(x)+cos(x)=0 (рис. 4.1):
Рис 4.1. Поиск корня нелинейного алгебраического уравнения
Хотя уравнение имеет бесконечное количество корней, функция root() находит (с заданной точностью) только один из них, лежащий наиболее близко к х=0.6. Если задать другое начальное значение, то и решением будет другой корень уравнения. Таким образом, для поиска корня средствами Mathcad требуется его предварительная локализация. Это связано с особенностями выбранного численного метода, который является методом секущих и состоит в следующем (рис. 4.2): - начальное приближение принимается за 0-е приближение к корню: х0=х; - выбирается шаг h=TOL∙х и определяется первое приближение к корню x1=x0+h; - через эти две точки (f(x0) и f(x1)) проводится секущая - прямая линия, которая пересекает ось х в некоторой точке х2. Эта точка принимается за второе приближение; - новая секущая проводится через первую и вторую (f(x1) и f(x2)) точки, тем самым определяя третье приближение, и т. д.; - если на каком-либо шаге оказывается, что уравнение выполнено, т. е. if |(x)|<TOL, то итерационный процесс прерывается, и х выдается в качестве решения.
Рис. 4.2. Иллюстрация метода секущих
Чем меньше константа TOL, тем ближе к нулю будет значение f(x) в найденном корне, но тем больше времени будет затрачено вычислительным процессором Mathcad на его поиск. Если уравнение неразрешимо, то при попытке найти его корень будет выдано сообщение об ошибке. Кроме того, к ошибке или выдаче неправильного корня может привести и попытка применить метод секущих в области локального максимума или минимума f(х). В этом случае секущая может иметь направление, близкое к горизонтальному, выводя точку следующего приближения далеко от предполагаемого положения корня. Приближенное решение уравнений
Когда невозможно найти решение с помощью функции Find( ), можно попытаться потребовать вместо точного выполнения уравнений условий минимизировать их невязку. Для этого следует в вычислительном блоке вместо функции Find( ) использовать функцию Minerr( ), имеющую тот же самый набор параметров и ту же методику применения: - x1:=C1 ... хm: =Cm – начальные приближения для неизвестных; - Given - ключевое слово; - система алгебраических уравнений и неравенств, записанная логическими операторами; - Minerr (x1,... ,хm) - приближенное решение системы относительно переменных х1;... ,хм, минимизирующее невязку системы уравнений. В функции Minerr( ) реализованы те же самые алгоритмы, что и в функции Find( ), иным является только условие завершения работы численного метода. Поэтому пользователь может тем же самым образом, с помощью контекстного меню, выбирать численный алгоритм приближенного решения для функции Minerr( ). Пример использования функции Minerr( ) показан на рис. 4.3.
Рис. 4.3. Приближенный метод решения уравнения, имеющего корень (x=0, y=0) Уравнение k·x2+y2=0 при любом значении коэффициента k имеет единственный точный корень (х=0,у=0). Тем не менее, при попытке решить его функцией Find( ) для больших k происходит генерация ошибки "No solution was found" (Решение не найдено). Это связано с иным поведением функции f(x,y)=k·x2+y2 вблизи ее корня, поэтому и найти корень изложенными в предыдущем разделе градиентными методами сложнее, поскольку вблизи корня производные f(х,у) близки к нулю, и итерации могут уводить предполагаемое решение далеко от корня.
Задание 2. Решить два нелинейных уравнения с точностью до 0,0001. Выполнить проверку решения.
1. а) 2. а) 3. а) 4. а) 5. а) 6. а) 7. а) 8. а) 9. а) 10. а) 11. а) 12. а) 13. а) 14. а) 15. а) 16. а) 17. а) 18. а) 19. а) 20. а) 21. а) 22. а) 23. а) 24. а) 25. а) 26. а)
Задание 2. Решить систему нелинейных уравнений с точностью до 0,0001. Приближенное решение системы найти графически.
1.
3. 5.
7.
9.
11.
13.
15.
17.
19.
21.
23.
25.
Задание 3. Решить систему линейных уравнений с точностью до 0,01. Выполнить проверку решения.
1.
3.
5.
7.
9.
11.
13. 15.
17.
19.
21.
23.
25.
Примеры выполнения заданий №2÷№4 даны в конце методички. .
|






 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
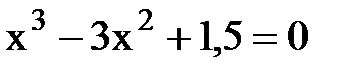 б)
б) 
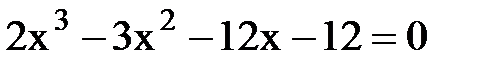 б)
б) 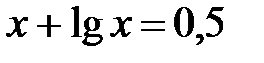
 б)
б) 
 б)
б) 
 б)
б) 
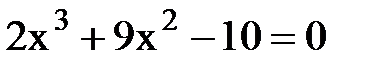 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 
 б)
б) 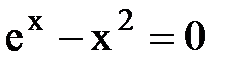
 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 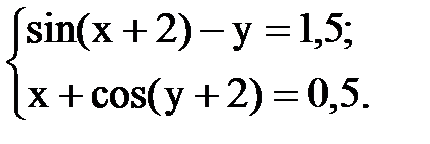
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 
 2.
2. 
 4.
4. 
 6.
6. 
 8.
8. 
 10.
10. 
 12.
12. 
 14.
14. 
 16.
16. 
 18.
18. 
 20.
20. 
 22.
22. 
 24.
24. 
 26.
26. 