ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Решение по нескольким целевым функциям
Лабораторная работа №2. Двойственность в задачах линейного программирования. Анализ полученных решений Цель работы Решение двух задач вариантного анализа для задач распределения ресурсов: - параметрического анализа, в ходе которого решаются задачи при различных значениях одного из параметров; - поиска решений по нескольким целевым функциям.
Задание на лабораторную работу Провести вариантный анализ для задачи распределения ресурсов.
Порядок выполнения работы Анализ оптимального решения выполняется на основании применения положений симплекс-метода и начинается после успешного решения задачи, когда на экране появляется диалоговое окно Результат поиска решения. Решение найдено. С помощью этого окна можно вызвать отчеты трех типов: 1. результаты; 2. устойчивость; 3. пределы. Отчет по результатам состоит из трех таблиц (рисунок 2.1):
Рисунок 2.1 Таблица сведений о целевой функции. В столбце Исходное значение приведены значения целевой функции до начала вычислений. Таблица значений искомых переменных, полученных в результате решения задачи. Таблица результатов оптимального решения для ограничений и для граничных условий. Для Ограничений в графе Формула приведены зависимости, которые были введены в диалоговое окно Поиск решения; в графе Значение приведены величины использованного ресурса; в графе Разница показано количество неиспользованного ресурса. Если ресурс используется полностью, то в графе Состояние указывается связанное; при неполном использовании ресурса в этой графе указывается не связан. Для граничных условий приводятся аналогичные величины с той лишь разницей, что вместо величины неиспользованного ресурса показана разность между значением переменной в найденном оптимальном решении и заданным для нее граничным условием. Отчет по устойчивости состоит из двух таблиц (рисунок 2.2):
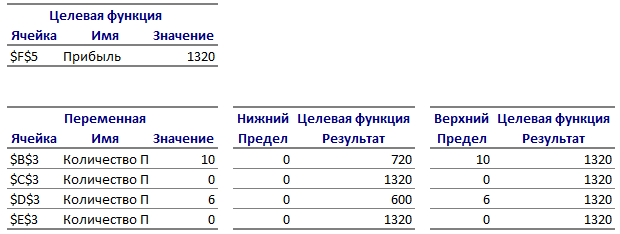
Рисунок 2.2 В таблице Ячейки переменных приводятся следующие значения для переменных: - результат решения задачи; - градиент (редуцированная стоимость), т.е. дополнительные двойственные переменные, которые показывают, насколько изменяется целевая функция при принудительном включении единицы этой продукции в оптимальное решение; В таблице Ограничения приводятся аналогичные значения для ограничений: - величина использованных ресурсов; - теневая цена, т.е. двойственные (маргинальные) оценки ресурсов (множители Лагранжа), которые показывают, как изменится целевая функция при изменении ресурсов на единицу; В отчете по пределам приводятся значения xj в оптимальном решении; приводятся нижние пределы изменения значений xj. Кроме того, в отчете указаны значения целевой функции при выпуске данного типа продукции на нижнем пределе (рисунок 2.3).
Рисунок 2.3
2. Параметрический анализ для задачи распределения ресурсов выполняется при различных вариантах изменения параметров модели (коэффициентов целевой функции, вектора ограничений, коэффициентов матрицы ограничений). Выполним параметрический анализ задачи, решая ее при различных значениях имеющихся финансов (т.е. будем варьировать параметры вектора ограничений). Под параметрическим анализом будем понимать решение задачи оптимизации при различных значениях того параметра, который ограничивает улучшение целевой функции. Алгоритм 1. Выполнение параметрических расчетов. Решить задачу, изменяя значения параметра «финансы»: 50, 100, 150, 200, 250. - Вызвать на экран таблицу с результатом решения задачи из лабораторной работы №1 (пример 1). - Удалить результат решения, находящийся в В3:Е3. - Ввести в ячейку G10 = 50. - Сервис, Поиск решения... - Выполнить. - На экране: диалоговое окно Результаты поиска решения - Сохранить сценарий... (рисунок 2.4)
Рисунок 2.4 Ввести имя сценария Финансы = 50 Аналогично решить задачи для последующих вариантов, при этом вводить имя сценария, соответствующего значению финансов. Представление результатов решения вызывается следующим образом: Вкладка Данные → раздел Работа с данными → кнопка Анализ “что если” → Диспетчер сценариев (рисунок 2.5).
Рисунок 2.5 На экране: диалоговое окно Диспетчер сценариев (рисунок 2.6).
Рисунок 2.6
Выбираем кнопку Отчет... На экране: диалоговое окно Отчет по сценарию (рисунок 2.7).
Рисунок 2.7 Выбираем тип отчета Структура На экране: отчет Структура сценария для всех значений финансов, принятых в таблице вариантов. Для удобства дальнейшей работы необходимо выполнить редактирование структуры сценария. После этого отчет Структура сценария будет выглядеть так, как показано на рисунке 2.8:
Рисунок 2.8 Построить гистограмму для искомых переменных: - Выделить C3:H9. - Вкладка Вставка → Гистограмма. - Выполнить форматирование гистограммы На рисунке 2.9 представлена гистограмма, на основании которой можно сделать следующие выводы:
Рисунок 2.9 При различном финансировании в план входит продукция различных видов, однако ни в один вариант не входит выпуск продукции П2. Это объясняется тем, что при высоком потреблении ресурсов прибыль от ее производства ниже, чем от производства других видов продукции. Для значений финансов 50, 150, 200 величина выпускаемой продукции является дробной. Такое положение допустимо при планировании, например, выпуска ткани, добычи нефти и т.д. При выпуске штучной продукции, очевидно, что в плане должны быть целые числа. Для получения такого плана следует решать задачу целочисленного программирования. Построить смешанную диаграмму для целевой функции и требуемого сырья (рисунок 2.10)
Рисунок 2.10 На основании данной диаграммы можно сделать следующие выводы. Увеличение финансирования дает увеличение прибыли, что вполне естественно. При увеличении финансирования, начиная со 150, происходит уменьшение потребляемого сырья. Такой результат является неожиданным, но это не ошибка. Это следствие того, что выпуск П3, П4, обеспечивающих увеличение прибыли, требует при этом меньшего потребления сырья.
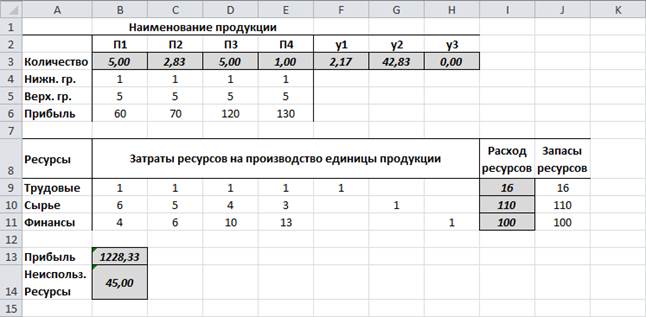
Решение по нескольким целевым функциям В задаче распределения ресурсов возможны две постановки: - максимизация результата при заданных ресурсах; - минимизация используемых ресурсов при заданном результате. Как решать такие задачи в EXCEL рассмотрим на примере. Назначим граничные условия на все виды выпускаемой продукции 1 £ П*£ 5, которые введем в ячейки В4:Е5. Сформулируем целевые функции для решения задачи в двух постановках. Целевая функция при максимизации прибыли, которая остается без изменений, введена в В13. Для решения задачи при минимизации используемых ресурсов в математическую модель введем дополнительные переменные и запишем задачу в следующем виде: F2 = y1 + y2 + y3 ® max x1 + x2 + x3 + x4 + y1 = 16 6x1 + 5x2 + 4x3 + 3x4 + y2 = 110 4x1 + 6x2 + 10x3 + 13x4 + y3 = 100 1 £ xj £ 5; j = 1, 2, 3, 4 Здесь y1, y2,, y3 – это дополнительные переменные, которые определяют величину неиспользованного ресурса. Следовательно, если мы хотим минимизировать используемые ресурсы, то должны максимизировать неиспользуемые ресурсы. Целевая функция для такой для такой постановки введена в ячейку В14. Решение задачи по нескольким целевым функциям производится по следующему алгоритму. - ввести условия задачи и все целевые функции в таблицу для ввода условий задачи; - назначить первую целевую функцию и ввести ограничения и граничные условия; - решить задачу последовательно по всем целевым функциям (в нашем примере их две) аналогично параметрическому анализу (рисунки 2.11-2.12).
Рисунок 2.11
Рисунок 2.12
Назначить целевую функцию В13 - Сохранить сценарий - Ввести имя «Max прибыль». Назначить целевую функцию В14 - Сохранить сценарий - Ввести имя «Min ресурсы» Вывести Отчет по сценарию (рисунок 2.13). Выполнить форматирование отчета.
Рисунок 2.13 Представить результаты в виде трехмерной гистограммы.
|