 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| C. Синтез КИХ-фильтра ФНЧ с произвольными требованиями к АЧХ (входные параметры function-файла).
Московский Технический Университет Связи и Информатики (МТУСИ)
Кафедра радиотехнических систем Лабораторная работа №5 Синтез КИХ-фильтров методом окон
Выполнила студентка группы БРА1101 Тюрина А.В. Проверила Мирошникова Н.Е.
Москва 2013 ЦЕЛЬ РАБОТЫ
Изучить процедуру синтеза КИХ-фильтров методом окон и овладеть программными средствами MATLAB для синтеза и анализа КИХ-фильтров; познакомиться с GUI WinTool (Window Design and Analysis Tool – средство создания и анализа окон) и GUI FVTool (Filter Visualization Tool – средство визуализации фильтра).
ИСХОДНЫЕ ДАННЫЕ Таблица 1.Требования к АЧХ ФНЧ
Таблица 2.Требования к АЧХ ФВЧ
Таблица 3.Требования к АЧХ ПФ
Таблица 4.Требования к АЧХ РФ
ДОМАШНЕЕ ЗАДАНИЕ Вариант 12.
C. Синтез КИХ-фильтра ФНЧ с произвольными требованиями к АЧХ (входные параметры function-файла). Для проверки выполнения требований к АЧХ использовать function-файл check_low. Вывести графики ИХ, АЧХ и ФЧХ с помощью function-файла plot_fir. Выходным параметром function-файла является вектор коэффициентов КИХ-фильтра.
function [b] = Untitled1( input_args ) clc clear disp('п.1. ВВОД ТРЕБОВАНИЙ К АЧХ ФНЧ') disp('Введите требования к АЧХ') DATA=0; while DATA==0; Fs = input('Fs = '); % ЧАСТОТА ДИСКРЕТИЗАЦИИ (Гц) ft = input('ft = '); % ГРАНИЧНАЯ ЧАСТОТА ПП (Гц) fk = input('fk = '); % ГРАНИЧНАЯ ЧАСТОТА ПЗ (Гц) d1 = input('d1 = '); % МАКСИМАЛЬНО ДОПУСТИМОЕ ОТКЛОНЕНИЕ В ПП d2 = input('d2 = '); % МАКСИМАЛЬНО ДОПУСТИМОЕ ОТКЛОНЕНИЕ В ПЗ disp('Проверьте ПРАВИЛЬНОСТЬ ввода ИСХОДНЫХ ДАННЫХ') disp('При ПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 1') disp('При НЕПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 0 и ПОВТОРИТЕ ввод') DATA = input('--> '); end m = [1 0]; % ВЕКТОР ЗНАЧЕНИЙ ИДЕАЛЬНОЙ АЧХ f = [ft fk]; % ВЕКТОР ГРАНИЧНЫХ ЧАСТОТ ripple = [d1 d2]; % ВЕКТОР МАКСИМАЛЬНО ДОПУСТИМЫХ ОТКЛОНЕНИЙ [R,wc,beta,ftype] = kaiserord(f,m,ripple,Fs);% ВЫЧИСЛЕНИЕ ПАРАМЕТРОВ ОКНА КАЙЗЕРА disp(['R = ' num2str(R)]) % ОЦЕНКА ПОРЯДКА КИХ-ФИЛЬТРА disp(['wc = ' num2str(wc)]) % НОРМИРОВАННАЯ ЧАСТОТА РАЗРЫВА disp(['beta = ' num2str(beta)]) % ПАРАМЕТР ОКНА КАЙЗЕРА disp(['ftype = ' char(ftype)]) % ТИП КИХ-ФИЛЬТРА disp(' ') pause disp('п.2. СИНТЕЗ КИХ-ФИЛЬТРА ФНЧ') b = fir1(R,wc,ftype,kaiser(R+1,beta),'noscale'); % КОЭФФИЦИЕНТЫ КИХ-ФИЛЬТРА ФНЧ disp(' ') disp([' Синтезирован КИХ-фильтр ФНЧ порядка R = ' num2str(R)]) disp(' ') disp('Для вывода ФАКТИЧЕСКИХ максимальных отклонений АЧХ') disp('в ПП (dp) и ПЗ (ds) и ЗАДАННЫХ отклонений d1 и d2 нажмите <ENTER>') pause [dp,ds] = check_low(b,ft,fk,Fs); % ВЫЧИСЛЕНИЕ ФАКТИЧЕСКИХ МАКСИМАЛЬНЫХ ПО МОДУЛЮ ОТКЛОНЕНИЙ В ПП И ПЗ disp(' ') disp(['dp = ' num2str(dp) ' ds = ' num2str(ds)]) disp(['d1 = ' num2str(d1) ' d2 = ' num2str(d2)]) disp(' ') disp('Для продолжения нажмите <ENTER>') pause disp('п.3. АНАЛИЗ ХАРАКТЕРИСТИК КИХ-ФИЛЬТРА ФНЧ') disp(' ') disp(' Для вывода ГРАФИКОВ ИХ, АЧХ и ФЧХ нажмите <ENTER>') pause figure('Name','Lowpass FIR Filter - Impulse Response, Magnitude, Phase','NumberTitle', 'off') plot_fir(R,b,Fs) % ПОСТРОЕНИЕ ГРАФИКОВ ИХ, АЧХ и ФЧХ disp(' ') disp('СИНТЕЗ КИХ-ФИЛЬТРА ФНЧ ЗАВЕРШЕН') end
п.1. ВВОД ТРЕБОВАНИЙ К АЧХ ФНЧ Введите требования к АЧХ Fs = 5200 ft = 200 fk = 800 d1 = 0.01 d2 = 0.05 Проверьте ПРАВИЛЬНОСТЬ ввода ИСХОДНЫХ ДАННЫХ При ПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 1 При НЕПРАВИЛЬНЫХ ИСХОДНЫХ ДАННЫХ введите 0 и ПОВТОРИТЕ ввод --> 1 R = 20 wc = 0.19231 beta = 3.3953 ftype = low
п.2. СИНТЕЗ КИХ-ФИЛЬТРА ФНЧ
Синтезирован КИХ-фильтр ФНЧ порядка R = 20
Для вывода ФАКТИЧЕСКИХ максимальных отклонений АЧХ в ПП (dp) и ПЗ (ds) и ЗАДАННЫХ отклонений d1 и d2 нажмите <ENTER>
dp = 0.0063574 ds = 0.0087982 d1 = 0.01 d2 = 0.05
Для продолжения нажмите <ENTER> п.3. АНАЛИЗ ХАРАКТЕРИСТИК КИХ-ФИЛЬТРА ФНЧ
Для вывода ГРАФИКОВ ИХ, АЧХ и ФЧХ нажмите <ENTER>
СИНТЕЗ КИХ-ФИЛЬТРА ФНЧ ЗАВЕРШЕН
2С. Вычисление реакции КИХ-фильтра ФНЧ на воздействие в виде периодической последовательности с периодом
Входными параметрами function-файла являются: · вектор коэффициентов КИХ-фильтра (см. п. 1C); · частота дискретизации · амплитуды гармоник А1 и А2; · частоты гармоник Вводимые значения частот должны быть согласованы с граничными частотами в требованиях к АЧХ КИХ-фильтра. Частота
Реакцию КИХ-фильтра Вывести графики воздействия и реакции КИХ-фильтра. Выходными параметрами function-файла являются векторы отсчетов воздействия и реакции.
function [x,y] = Untitled2(b,Fs,fk,ft) DATA=0; while DATA==0; A1 = input('A1 = '); % A2 = input('A2 = '); % Амплитуды гармоник f1 = input('f1 = '); % f2 = input('f2 = '); % Частоты гармоник (Гц) disp('Проверка данных') disp(' ') if f1<=ft & f2>=fk disp('Частоты гармоник введены корректно') DATA = 1; else disp ('Частоты гармоник введены некорректно, повторите ввод') DATA = 0; end end N=64; n=0:(N-1); x=A1*cos(2*pi*f1*n/Fs)+A2*cos(2*pi*f2*n/Fs); y=filter(b,1,x); subplot(2,1,1), stem(n,x,'fill','MarkerSize',3), grid xlabel('n'), ylabel('x(n)'), title('Input Signal') subplot(2,1,2), stem(n,y,'fill','MarkerSize',3), grid xlabel('n'), ylabel('y(n)'), title('Output Signal ') end
>> [x,y] = My1(b,Fs,fk,ft) A1 = 1 A2 = 10 f1 = 162.5 f2 = 2600 Проверка данных
Частоты гармоник введены корректно
|
:
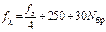
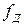(она должна совпадать с заданной в требованиях к АЧХ КИХ-фильтра);
и 
.
вычислить с помощью функции filter.