 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ПРИМЕР ПРИМЕНЕНИЯ КОРРЕЛЯЦИОННО-РЕГРЕССИРННОГО АНАЛИЗА ДЛЯ ОЦЕНКИ ДЕЯТЕЛЬНОСТИ КОНКРЕТНОГО ПРЕДПРИЯТИЯ 12
1 Экономическая постановка задачи
При анализе финансовой состояния предприятия необходимо оценить факторы, влияющие на обеспеченность предприятия финансовыми ресурсами. На РПУП «Торгмаш» основными источниками, определяющими формирование финансовых ресурсов, являются собственные оборотные средства. В результате произведенного анализа финансовых показателей предприятия было установлено, что на РПУП «Торгмаш» постоянно возрастает потребность в собственных оборотных средствах, что влияет на сокращение использования финансовых ресурсов и ведет к неустойчивому финансовому положению предприятия. Поэтому следует произвести экономические исследования, цель которых будет состоять в выявлении показателей, таких как – кредиторская задолженность и сумма оборотных активов, влияющих на изменения потребности в собственных оборотных средствах РПУП «Торгмаш». Таблица 1 – Исходные данные, млн. руб.
На основании приведенных в таблице 1 данных необходимо: а) построить математическую модель, определяющую зависимость между потребностью в собственных оборотных средствах, кредиторской задолженностью и суммой оборотных активов; б) определить уравнение связи этих показателей; в) спрогнозировать, как измениться потребность в собственных оборотных средствах в 2007 и 2008 году.
2 Математическая постановка задачи
В экономике каждому значению одной переменной соответствует множество значений. Связи между переменными можно изучать методом корреляционного и регрессионного анализа. Корреляционная связь является частным случаем статистической связи, при которой изменение среднего значения результативного признака обусловлено изменением значений факторного признака (парная корреляция) или множества факторных признаков (множественная корреляция). Для оценки тесноты связи (связь отсутствует, слабая, умеренная, сильная), определения ее направленности (связь прямая или обратная), а также формы (связь линейная, параболическая, гиперболическая, степенная) используется корреляционно-регрессионный метод. Корреляционно-регрессионный анализ позволяет количественно измерить тесноту, направление связи (корреляционный анализ), а также установить аналитическое выражение зависимости результата от конкретных факторов при постоянстве остальных действующих на результативный признак факторных признаков (регрессионный анализ). Задачи проведения корреляционно-регрессионного анализа по предложенной модели (таблица 1) следующие: а) определить уравнение связи между кредиторской задолженностью (x1), суммой оборотных активов (x2) и потребностью в собственных оборотных средствах (y); б) вычислить коэффициенты корреляции и проанализировать тесноту связи между ними; в) оценить качество построенной модели, вычислить среднюю ошибку аппроксимации и коэффициент детерминации; г) дать экономическую интерпретацию полученных результатов; д) определить точечные интервальные прогнозные оценки факторов модели на 2 года вперед.
3 Решение задачи в среде Excel
Чтобы определить, как повлияет изменение факторов x1 и x2 на изменение величины y, необходимо вычислить матрицу коэффициентов парной корреляции (таблица 2). Данную матрицу находим с помощью команды «Сервис / Анализ данных / Корреляция».
Таблица 2 – Матрица коэффициентов парной корреляции
Данные таблицы 2 указывают на явление мультиколиниарности (rx1x2 = 0,84102043, следовательно, rx1x2 > 0,8). Полученная связь делает вычисление параметров модели затруднительным, поэтому, чтобы избавиться от мультиколиниарности в анализируемую модель необходимо включить один из факторов, который теснее связан с y. В этом случае, в модели останется лишь переменная x1, т.к. она наиболее тесно связана с y. Парный коэффициент корреляции (ryx1)определяется по формуле 1.1
Таблица 3 – Промежуточные расчеты коэффициента парной корреляции
Анализ матрицы коэффициентов показывает, что зависимая переменная х1 имеет весьма тесную связь с у (rуx1= 0,934486151). Следовательно, величина кредиторской задолженности весьма тесно связана с величиной потребности в собственных оборотных средствах предприятия. Однако показатель тесноты связи может искажаться под действием случайных величин. Это вызывает необходимость поверки его существенности с помощью t-критерия Стьюдента (tr), табличное значение которого (tk) равно 2,353
где n – количество наблюдений.
Таким образом, произведенные расчеты показали, что tr > tk, поэтому величина коэффициента корреляции признается существенной. Для отображения линейной зависимости переменных используется уравнение регрессии: y = a0 + a1*x1, (1.3) где а0 и а1 – коэффициенты регрессии. Необходимо рассчитать такие значения коэффициентов а0 и а1, при которых сумма квадратов отклонений расчетных значений y от фактических была бы минимальной
В результате произведенных расчетов в среде Excel а0 = 294,4741754 и а1 = 1,77. Значит уравнение регрессии примет вид (формула 1.6) y= 294,47+1,77x1, (1.6) Применяя команду «Сервис / Анализ данных / Регрессия» можно найти все неизвестные параметры (рисунок 1), характеризующие уравнение регрессии и зависимость между параметрами.
Рисунок 1 – Регрессионная статистика Для оценки качества подбора линейной функции рассчитывается коэффициент детерминации (R2), который характеризует долю дисперсии результативного показателя y, объясняемую регрессией, в общей дисперсии результативного показателя. Т.е. коэффициент детерминации позволяет проверить, не упущен ли какой-либо фактор, оказывающий заметное влияние на показатель y. R2 = ryx12, (1.7) По расчетам в среде Excel R2 = 0,873264367(следовательно, R2 > 0,7) , это означает, что 87% рассеивания зависимых переменных объясняется линейной регрессией, а 13% рассеивания y остались необъяснимы. Эти 13% рассеивания у могут быть вызваны либо случайными ошибками эксперимента, либо тем, что линейная регрессионная модель плохо согласуется с экспериментальными данными. Чтобы проверить значимость уравнения регрессии используется критерий Фишера (F)
где k – количество степеней свободы.
Табличное значение F при указанных значениях: Fтабл = 10,1. Так как расчетное F>Fтабл, то приходим к выводу, что линейная модель регрессии согласуется с экспериментальными данными (имеет линейный вид), коэффициенты регрессии значимы. Важную роль при оценке влияния факторов играют коэффициенты регрессионной модели. Но непосредственно с их помощью нельзя сопоставить факторы по степени их влияния на зависимую переменную из-за различия единиц измерения и разной степени их колеблемости. Для устранения таких различий применяется коэффициент эластичности (формула 1.9)
Коэффициент эластичности показывает, насколько процентов измениться y при увеличении x1 на 1%. Полученные значения эластичности свидетельствуют о том, что при уменьшении кредиторской задолженности на 1%, потребность предприятия в собственных оборотных средствах уменьшится на 0,93%. Значимость отдельных коэффициентов проверяем с помощью Т-критерия (ta1) путем проверки гипотезы
где Sa1 – ошибка коэффициента регрессии:
Таблица .4 – данные для расчета ошибки коэффициента регрессии
Данные значения можно также определить при помощи следующей команды «Сервис / Анализ данных / Регрессия»(рисунок 5.1) в столбце t-статистика. Так как tкр=1,86, следовательно ta1 > tкр, то коэффициенты уравнения линейной регрессии значимы. Для принятия серьезных решений в экономике и бизнесе необходим прогноз и предвидение развития экономической ситуации. Для того чтобы предвидеть будущее, надо хорошо знать прошлое и присущие ему закономерности (временные ряды). Во временном ряде содержится информация об особенностях и закономерностях протекания процесса, а статистический анализ позволяет выявить и использовать их для оценки характеристик процесса в будущем, т.е. для прогнозирования. При анализе временных рядов широко применяются графические методы. Визуальный анализ графика временного ряда позволяет сделать выводы о наличии тренда и его характере. В Excel для анализа временных рядов можно использовать «Мастер диаграмм». Модель для фактора кредиторской задолженности х1 определяется с помощью метода наименьших квадратов. Аппроксимирующей функцией выступает линейная функция. Получаем следующую модель (формула 1.12) x1 = 526,7*t + 774,9, (1.12) где t – период наблюдения. По данному уравнению получим прогноз на два года вперед. Для этого построим график временного ряда и линию тренда.
Рисунок 2 – График временного ряда кредиторской задолженности и ее линия тренда
Для временного ряда кредиторской задолженности х1 рассчитываются следующие прогнозные значения: при t = 6 х1 = 3935,1; при t = 7 х1 = 4461,8 Для получения прогнозных оценок потребности предприятия в собственных оборотных средствах на 2 года вперед необходимо в модель y= 294,47+1,77x1 подставить найденные прогнозные значения х1: при t = 6 у =7259,597; при t = 7 у =8191,856 Выводы Таким образом, проведя корреляционно-регрессионный анализ, были получены следующие выводы: а) величина кредиторской задолженности весьма тесно связана с величиной потребности в собственных оборотных средствах, коэффициент корреляции между этими величинами равен rуx1= 0,934486151, величина коэффициента корреляции признана существенной; б) уравнение регрессии имеет вид: y= 294,47+1,77x1; в) при проведении анализа было установлено, что при уменьшении кредиторской задолженности на 1%, потребность предприятия в собственных оборотных средствах уменьшится на 0,93%; г) коэффициент детерминации R2 = 0,873264367(следовательно, R2 > 0,7), это означает, что 87% рассеивания зависимых переменных объясняется линейной регрессией, а 13% рассеивания y остались необъяснимы. Значение критерия Фишера подтверждает, что линейная модель регрессии согласуется с экспериментальными данными (имеет линейный вид), коэффициенты регрессии значимы. д) при прогнозировании на 2007 и 2008 году были найдены исследуемые величины: так величина кредиторской задолженности в будущем будет возрастать и составит в 2007г. – 3935,1 млн. руб., в 2008г. – 4461,8 млн. руб., а потребность РПУП «Торгмаш» в собственных оборотных средствах в 2007г. составит 7259,597 млн. руб., в 2008г. – 8191,856 млн. руб. Эти данные лишний раз подтверждают нестабильное финансовое положение субъекта хозяйствования, чтобы выйти из кризисного состояния предприятию необходимо направлять основную деятельность на пополнение собственных оборотных средств, за счет которых изменятся показатели деловой активности в направлении роста, а также увеличится величина основного финансового ресурса – прибыли. 12 |



 , (1.1)
, (1.1) , (1.2)
, (1.2)
 , (1.4)
, (1.4) , (1.5)
, (1.5)
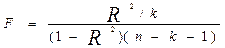 , (1.8)
, (1.8)
 , (1.9)
, (1.9)
 (1.10)
(1.10) , (1.11)
, (1.11)

