 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Сопоставление численных методов решения нелинейных уравнений
Лабораторная работа №1 Цель: освоить алгоритмы численных методов решения нелинейных уравнений, условия их применения и технологию сопоставления.
Задание: Дано уравнение
Таблица 1
Рисунок 1
На основе численных результатов сопоставить методы по скорости сходимости, понимая под скоростью сходимости число итераций n, необходимых для достижения заданной точности ε. Полученными экспериментальными данными подтвердить теоретические положения.
Варианты заданий: 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20.
Ход выполнения лабораторной работы: 1 осуществить отделение корней, используя любой из известных методов: 1.1 аналитический метод; 1.2 графический метод; 1.3 табулирование с шагом h.
2 Уточнить изолированные корни используя: 2.1 метод бисекций и хорд для всех ε; 2.2 метод бисекций и Ньютона для всех ε; 2.3 метод Ньютона и хорд для всех ε.
1.1 Отделение корней аналитическим методом
Рассмотрим уравнение
на отрезке [-3,3]. 1) Находим производную
2) Решаем уравнение
Корни уравнения
3) Рассмотрим отрезки
Проанализируем поведение функции
f (-3)= -13<0.
Следовательно, корень существует и единственный На отрезке
Следовательно, корень существует и единственный. . На отрезке
f (3)=17>0
Следовательно, корень существует и единственный.
1.2 Отделение корней графическим методом
Строим качественно график функции (в любом математическом пакете)
на отрезке [-3,3].
Из графика видно функция
пересекается с осью ОХ три раза в отмеченных точках. Следовательно, берем промежутки [-2,4; -2,1], [0,4; 0,9], [1,5; 1,8].
1.3 Отделение корней табулированием функции
1) Проведем табулирование функции
с шагом
Таблица 1- Табулирование функции
Вывод: нашли три отрезка, содержащие корни. Уравнение
третей степени, следовательно, различных корней не более 3, т.е. каждый из выделенных отрезков содержит по одному корню: [-2,4;-2,2], [0,4;0,6], [1,6;1,8]. 2) Если количество отрезков не совпадает с количеством корней, то необходимо осуществить табулирование функции
(разные знаки на концах).
2 Уточнение изолированных корней
2.1Уточнение корней методом бисекций
Алгоритм: 1. 2. 3. Если 1. 2. Если 3. Иначе: 1. 2. Если 3. Если
2.2Уточнение корней методом Ньютона
Алгоритм: 1. 2. Выбрать 3. Пока 1. 2.
2.3 Уточнение корней методом хорд
Алгоритм: 1. 2. Выбрать 3. Пока 1. 2.
Выводы (образцы): 1. Подстановка полученных корней в заданное уравнение показала, что алгоритм реализован правильно. 2. Анализ таблицы 1 показал, что при увеличении заданной точности от 3. На основе анализа таблицы можно сделать вывод, что метод1 сходится быстрее чем метод2 при заданной точности от |



 на отрезке
на отрезке  . Используя численные методы: метод бисекций, метод Ньютона, метод хорд осуществить его решение с заданной точностью ε = 10-3, 10-4, 10-5, 10-6, 10-7, 10-8. Полученное решение (для всех найденных корней) представить в сводной таблице (таблица 1) и изобразить графически (рисунок 1).
. Используя численные методы: метод бисекций, метод Ньютона, метод хорд осуществить его решение с заданной точностью ε = 10-3, 10-4, 10-5, 10-6, 10-7, 10-8. Полученное решение (для всех найденных корней) представить в сводной таблице (таблица 1) и изобразить графически (рисунок 1).




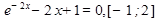













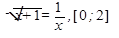


 .
. .
. .
.
 на отрезке
на отрезке  функция
функция  возрастает и имеет разные знаки на концах отрезка:
возрастает и имеет разные знаки на концах отрезка: ,
, . Функция
. Функция 
 .
.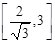 функция
функция  ,
,

 с шагом h.
с шагом h. .
.



 , то:
, то:
 , то:
, то:  – корень.
– корень.
 , то:
, то:  , вернуться к шагу 3
, вернуться к шагу 3 , то:
, то:  , вернуться к шагу 3
, вернуться к шагу 3
 :
:

 до
до  метод1 сходится медленнее в m раз.
метод1 сходится медленнее в m раз.