 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Описание метода и экспериментальной установки
Лабораторная работа 1.3.
ИЗУЧЕНИЕ РЕАЛЬНОГО СОУДАРЕНИЯ ШАРОВ. ОПРЕДЕЛЕНИЕ НЕОБРАТИМОЙ ПОТЕРИ
Библиографический список
1. Трофимова Т. И. Курс физики. М.: Высшая школа, 1985. 2. Савельев И.В. Курс общей физики. – М.: Наука, 1988. Т. 1.
Цель работы: экспериментальная проверка закона сохранения импульса при упругом и неупругом центральных ударах шаров, определение работы диссипативных сил. Приборы и принадлежности: лабораторная установка «Соударение шаров», штангенциркуль, линейка, динамометр.
Описание метода и экспериментальной установки
В механике под ударом понимают кратковременное взаимодействие двух или более тел, возникающее при их столкновении. При ударе происходит полный или частичный переход кинетической энергии тел в потенциальную энергию упругой деформации. Явление удара позволяет существенно увеличить силы взаимодействия. Например, при ударе слесарным молотком по наковальне на нее действует сила 105 Н. Так как сила разгона молотка перед ударом всего около 20 Н, то в результате удара достигается эффект трансформации силы в десятки тысяч раз. Этим вполне можно объяснить, почему человек с незапамятных времен стал использовать удар прежде, чем какое-либо другое механическое явление. Современное применение удара чрезвычайно многообразно и эффективно. В физической теории ударное взаимодействие рассматривают как процесс преобразования импульса и энергии. Физические основы ударного взаимодействия наглядно иллюстрируют соударения шаров со стенкой и между собой.
Прямой удар о неподвижную стенку изменяет направление полета шара на обратное в результате сложного процесса преобразования импульса и энергии. Первая часть этого процесса начинается с момента соприкосновения шара со стенкой. Если шар движется поступательно со скоростью V1, то все его точки дви В первой стадии удара ближайший к стенке слой вещества шара останавливается, а набегающие остальные слой сжимают его (рис. 1б). По мере расходования кинетической энергии на работу деформации толщина деформированного слоя растет. Иными словами, по телу шара с некоторой скоростью распространяется волна сжатия, которая спустя некоторое время достигнет свободного края, и деформированное состояние охватит весь объем шара. Аналогичная волна сжатия будет распространяться от места соприкосновения и в стенке. Следовательно, к концу первой стадии соударения кинетическая энергия шара будет израсходована на работу деформации шара и стенки. При абсолютно неупругом ударе упругих сил нет, действуют только диссипативные силы, и кинетическая энергия шара полностью расходуется на перемещение частей шара или стенки, или того и другого (на пластическую деформацию). В этом случае соударение заканчивается первой стадией, после которой наступает механическое равновесие сил. При абсолютно упругом ударе, наоборот, нет диссипативных сил и кинетическая энергия полностью преобразуется в потенциальную энергию упругой деформации и система стенка – шар не может оставаться в равновесии. Начнется вторая стадия соударения, при которой силы упругости последовательно, от вершины к месту соприкосновения будут ускорять слои шара, т. е. по шару в направлении стенки побежит волна разряжения (рис. 1в). Такая же обратная волна, восстанавливающая форму стенки, побежит к месту соприкосновения и внутри стенки.
будет равен единице. Если к моменту восстановления формы шара обратная волна деформации в стенке не достигнет места соприкосновения с шаром, то шар оторвется при меньшей кинетической энергии Таким образом, коэффициент восстановления скорости шара
Время соударения, согласно изложенному, зависит от размеров шара и стенки, от скоростей распространения волн деформации в соударяющихся телах, от величины начальной кинетической энергии или количества движения. Кроме того, время соударения зависит от формы и размеров соударяющихся тел и от формы соприкасающихся при ударе частей этих тел.
Расчет времени соударения – задача сложная, но для геометрически правильных тел из однородного материала – теоретически разрешимая. Например, при ударе шара радиусом R по полубесконечному телу из стали (плотность r = 7,8 г/см3, модуль упругости E = 2.107 Н/см2 и коэффициент Пуассона e = 0,286) время соударения получают равным а наибольшую силу удара
Согласно этим формулам, для стального шарика, падающего на торец стальной болванки с высоты 10 см (со скоростью Таким, образом, зависимости времени соударения, силы удара от скорости шара до соударения, т. е. зависимости
Количество движения шара при нормальном ударе о стенку сначала уменьшится от значения
и по второму закону Ньютона средняя сила удара равна Косой удар о стенку отличается тем, что шар перед ударом движется по траектории (линия удара), образующей с нормалью к поверхности стенки угол a (угол падения или угол удара).
Если начальная скорость шара  , то вектор количества движения , то вектор количества движения  можно разложить на составляющие: нормальную к стенке можно разложить на составляющие: нормальную к стенке  и касательную к стенке и касательную к стенке 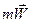 . При отсутствии трения скольжения шара по стенке составляющая . При отсутствии трения скольжения шара по стенке составляющая  в процессе соударения не изменяется, а нормальная составляющая в процессе соударения не изменяется, а нормальная составляющая  уменьшается до 0 в первой стадии и возрастает от 0 до уменьшается до 0 в первой стадии и возрастает от 0 до  - во второй стадии удара (рис. 2). - во второй стадии удара (рис. 2).
Легко подсчитать, что изменение количества движения шара при не вполне упругом ударе Если за время удара шар из-за трения не может скользить по стенке, то в области касания скорость W будет погашена и на шар подействует кратковременный вращательный момент силы трения.
При абсолютно упругом соударении (рис. 3) коэффициент восстановления скорости может быть равным единице, тогда V2 = V1, b = a, U2 = U1 и изменение количества движения шара будет равно
При соприкосновении шары деформируются по направлению линии удара, проходящей через центры шаров. За первую и вторую стадии соударения осуществляется перераспределение энергии между шарами и преобразование импульсов. Если для двух шаров с массами m и m' известны нормальные составляющие скоростей
и коэффициент восстановления k, то можно определить значения скоростей
скоростям. Так, для случая, изображенного на рис. 4 коэффициент восстановления будет равен Если траектории центров соударяющихся шаров совпадает
Абсолютно упругим называют такой удар, при котором механическая энергия тел не переходит в немеханические виды энергии, в частности, во внутреннюю энергию тел. При таком ударе кинетическая энергия частично или полностью переходит в потенциальную энергию упругой деформации, а затем тела возвращаются к первоначальной форме, отталкивая друг друга. В итоге, потенциальная энергия упругой деформации снова переходит в кинетическую энергию и тела разлетаются со скоростями, величина и направление которых определяются законом сохранения энергии и законом сохранения количества движения для замкнутой системы тел. Пусть шар ударяется о массивную неподвижную стенку. Если удар абсолютно упругий, кинетическая энергия после удара должна быть такой же, как до удара. Следовательно, шар должен иметь после удара такую же по величине скорость, как и до удара. В реальном же не вполне упругом ударе скорость тела после удара U будет несколько меньшей по величине, чем скорость до удара V. Очевидно, что величиной коэффициента восстановления скорости Рассмотрим реальный упругий центральный удар двух шаров (рис. 6). Прямую, проходящую через точку соприкосновения тел и нормальную к поверхности их соприкосновения, называют линией удара. Если линия удара проходит через центры масс обоих тел, то удар будет центральным.
Вывод расчетных формул
Если отвести шар массой m2, подвешенный на нити, на угол 90° от положения равновесия (рис.6), то свободно возвращаясь в нижнее положение этот шар приобретет кинетическую энергию
и скорость
где g — ускорение силы тяжести. С этой скоростью V2 шар массой m2 ударит во второй шар массы m1, тоже подвешенный на нити. В процессе удара между шарами перераспределяются импульс m2V2 и энергия. Шары разлетятся со скоростями U1 и U2. При реальном ударе действуют диссипативные силы, работа которых АД обычно отрицательна, приводит к потере телом энергии DW и определяется из закона сохранения энергии:
Если после удара шары m1 и m2 поднимаются на высоты h1
Как видно из рис.6 в треугольнике АВС
Отсюда
Аналогично можно записать и для шара массой m1:
Окончательно получаем:
Подставляя значения V2, U1 и U2 в (3), найдем значение работы диссипативных сил
Так как работа диссипативных сил всегда отрицательна, то ее величина может быть рассчитана по формуле
Скорости после реального удара U1 и U2 будут меньше скоростей после абсолютно упругого удара W1 и W2. Потери скоростей можно определить равными соответственно
Скорости W1 и W2 можно найти из решения системы уравнений, состоящей из закона сохранения импульса и закона сохранения механической энергии:
(8)
Поделим первое уравнение на второе и получим: Подставив полученное значение
Окончательно получаем выражения для скоростей шаров после абсолютно упругого удара
(9)
(10)
Подставим полученные значения в (7):
(11)
(12)
(13)
(14)
Описание установки Два шара разных масс
Порядок выполнения работы 1. Измерить штангенциркулем диаметры шаров
2. Измерить линейкой высоту подвеса каждого шара (Н1 3. Определить длины подвесов 4. Массы шаров могут быть указаны на основании прибора или необходимо измерить их с помощью лабораторного динамометра и оценить погрешность массы. 5. Шар меньшей массы ( 6. Результаты записать в таблицу наблюдений по форме:
Таблица 1
7. Рассчитать по методу Стьюдента доверительные интервалы 8. По (11), (12), (13) и (14) рассчитать значения 9. Рассчитать по (6) среднее значение потерянной механической энергии 10. Полагая погрешность ускорения силы тяжести
где: Dj — в радианах 11. Рассчитать
Контрольные вопросы 1. Почему силы, возникающие при ударе, велики? 2. Какие законы сохранения используются в данной работе? 3. Какие законы сохранения выполняются: а) при абсолютно упругом ударе? б) при абсолютно неупругом ударе? 4. Какие силы называются диссипативными? 5. Что такое коэффициент восстановления скорости и чему он равен для реального удара шаров? |









 до 0, затем возрастет от 0 до
до 0, затем возрастет от 0 до  (рис. 1а, 1г). Поэтому изменение количества движения за время удара t равно
(рис. 1а, 1г). Поэтому изменение количества движения за время удара t равно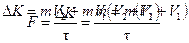





 и конечные скорости
и конечные скорости  . Рассматривая систему двух шаров как замкнутую, применяют законы сохранения количества движения и энергии.
. Рассматривая систему двух шаров как замкнутую, применяют законы сохранения количества движения и энергии.

 можно характеризовать отступление удара от абсолютно упругого и в конечном итоге – упругие свойства соударяющихся тел (шара и стенки или двух шаров). При абсолютно упругом ударе
можно характеризовать отступление удара от абсолютно упругого и в конечном итоге – упругие свойства соударяющихся тел (шара и стенки или двух шаров). При абсолютно упругом ударе  , при абсолютно неупругом равен нулю. Всякий реальный удар в большей или меньшей степени отличается от абсолютно упругого и, следовательно, характеризуется значением коэффициента восстановления скорости k, меньшим единицы.
, при абсолютно неупругом равен нулю. Всякий реальный удар в большей или меньшей степени отличается от абсолютно упругого и, следовательно, характеризуется значением коэффициента восстановления скорости k, меньшим единицы.
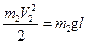 (1)
(1)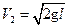 (2)
(2) — расстояние от точки подвеса до центра масс шара,
— расстояние от точки подвеса до центра масс шара,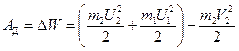 (3)
(3)




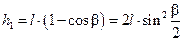
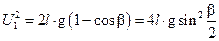
 (4)
(4) (5)
(5)
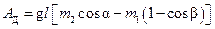 (6)
(6) (7)
(7)

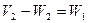
 в уравнение закона сохранения импульса, получим
в уравнение закона сохранения импульса, получим


 В условиях опыта относительная скорость шаров
В условиях опыта относительная скорость шаров  и
и  к моменту соударения равна
к моменту соударения равна  . Поэтому коэффициенты восстановления скорости шаров можно определить следующим
. Поэтому коэффициенты восстановления скорости шаров можно определить следующим и
и  (рис. 6). На основании прибора укреплены две шкалы, которые позволяют отсчитывать углы отклонения шаров. В положении равновесия шаров нити подвеса должны совпадать с нулевыми делениями шкал.
(рис. 6). На основании прибора укреплены две шкалы, которые позволяют отсчитывать углы отклонения шаров. В положении равновесия шаров нити подвеса должны совпадать с нулевыми делениями шкал.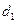 и
и 

 и
и  . Сравнить
. Сравнить  и
и  и, изменяя одну из высот подвеса (
и, изменяя одну из высот подвеса (  или
или  ), добиться равенства
), добиться равенства  . Величину
. Величину  .
.


















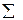



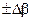 и
и  .
. ,
,  ,
,  и
и 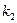 .
. .
. пренебрежимо малой, оценить относительную погрешность определения потерь энергии по формуле
пренебрежимо малой, оценить относительную погрешность определения потерь энергии по формуле (15)
(15)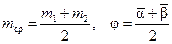
 и результат записать по форме
и результат записать по форме  , например, в виде
, например, в виде  , e = 5%, a = 0,9
, e = 5%, a = 0,9