 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА
ФГБОУ ВПО «КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» КАФЕДРА ФИЗИКИ ЛАБОРАТОРНАЯ РАБОТА № 110.2.10 ИЗУЧЕНИЕ ЭФФЕКТА ХОЛЛА В ПОЛУПРОВОДНИКАХ Методическое указание к выполнению лабораторных работ по разделу «Электричество и магнетизм» для студентов всех форм обучения по всем специальностям
Калининград ВВЕДЕНИЕ
В 1880 году американский физик Э. Холл обнаружил, что в проводнике, помещённом в магнитное поле, возникает разность потенциалов в направлении, перпендикулярном вектору магнитной индукции
Рис. 1
На рис. 1 изображена проводящая пластина, которую пронизывает магнитное поле с индукцией Эффект Холла наблюдается у металлов и полупроводников. У металлов, а также у полупроводников
a) б) Рис. 2 (а,б)
У проводников Так как вектор
Заряды, скопившиеся на верхней и нижней гранях пластины, создают электрическое поле напряжённостью
Когда устанавливается стационарное распределение зарядов в поперечном сечении проводника, эти две силы уравновешивают друг друга, т.е.
Из формулы плотности тока
где
Подставив данное выражение в формулу (1), получим
Тогда разность потенциалов между верхней и нижней гранями проводника, расстояние между которыми
Коэффициент пропорциональности в этой формуле
называется постоянной Холла. Уравнение (2) принимает вид
Т.е. разность потенциалов между гранями проводника, находящегося в поперечном магнитном поле, прямо пропорциональна толщине проводящей пластины Знак постоянной Холла совпадает со знаком заряда
Рис.3 Блок генераторов постоянных напряжений с наборным полем
проводимости, то по знаку постоянной Холла можно судить о том, какой из них является преобладающим. С помощью постоянной Холла можно также определить концентрацию носителей заряда, если характер проводимости и их заряд известны (например, для металлов):
МЕТОДИКА ПРОВЕДЕНИЯ ЭКСПЕРИМЕНТА 2.1. Задание на лабораторную работу Снять зависимость ЭДС Холла от магнитной индукции, определить постоянную Холла и концентрацию носителей заряда, приняв толщину пластины полупроводника
2.2. Порядок проведения эксперимента
2.2.1. Установите на панель блока БГННП миниблок «Датчик Холла». 2.2.2. Соберите схему эксперимента в соответствии с рис.3, подключив сначала мультиметр « 2.2.3. Присоединив блоки установки к сети ~ 220 2.2.4. Установите пределы измерений на «= 2.2.5. Запишите значение тока
2.2.6. Переключите мультиметр «А», как показано на рис.3 сплошной линией и установите на нём предел измерения 2.2.7. Соедините перемычкой гнёзда на панели, к которым был подключён мультиметр « 2.2.8. Установите регулятором выходного напряжения ток в катушке по мультиметру «
Таблица 1
Примечание.В случае затруднения при попытках точной установки указанных значений тока оставляйте на шкале мультиметра ближайшее значение, которое и заносите в таблицу.
2.2.9. Увеличивая ток в катушке до максимального значения с шагом 2.2.10. Выведите ручку регулятора выходного напряжения против часовой стрелки до упора, выключите блоки установки, отсоедините их от сети ~ 220 2.2.11. Рассчитайте среднее значение ЭДС Холла 2.2.12. Рассчитайте величину магнитной индукции в зазоре сердечника, на который намотана катушка, по формуле:
где
2.2.13. На миллиметровке формата
2.2.14. Рассчитайте постоянную Холла:
2.2.15. Рассчитайте концентрацию носителей заряда по формуле:
КОНТРОЛЬНЫЕ ВОПРОСЫ (ПРИМЕРНЫЕ)
3.1. Движение частиц в магнитном поле. 3.2. Сила Лоренца. Результирующая сила, действующая на заряженную частицу в электромагнитном поле. 3.3. Заряженная частица в скрещенных электрическом и магнитном полях. 3.4. Электропроводность материалов. 3.5. Эффект Холла. 3.6. Вывод рабочей формулы.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
4.1. Савельев И.В. Курс общей физики: учеб.пособие: в 3-х т./ И.В. Савельев.-М.,1992 – т.2. – 480 с. 4.2. Трофимова Т.И. Курс физики: учеб.пособие – 3–е изд., испр. и доп./ Т.И.Трофимова. – М.: Высш.шк.,1994. – 541с 4.3. Детлаф А.А. Курс физики: учеб.пособие / А.А.Детлаф, Б.М. Яворский. – М.: Высш. шк., 2000. – 717 с.
|



 и току
и току  .Объясняется это действием силы Лоренца.
.Объясняется это действием силы Лоренца.

 , направленное перпендикулярно чертежу от нас (обозначено крестиком). У отрицательных зарядов вектор скорости
, направленное перпендикулярно чертежу от нас (обозначено крестиком). У отрицательных зарядов вектор скорости  и ток
и ток  – типа, где носителями зарядов являются электроны, на верхней грани будут скапливаться избыточные отрицательные заряды, а нижняя грань, испытывая недостаток электронов, зарядится положительно (рис.2, а). В результате между верхней и нижней гранями проводника возникает определённая разность потенциалов
– типа, где носителями зарядов являются электроны, на верхней грани будут скапливаться избыточные отрицательные заряды, а нижняя грань, испытывая недостаток электронов, зарядится положительно (рис.2, а). В результате между верхней и нижней гранями проводника возникает определённая разность потенциалов  .
.
 – типа, у которых носителями тока являются дырки, имеющие положительный заряд, верхняя грань приобретает в магнитном поле положительный заряд, а нижняя – отрицательный (рис.2, б).
– типа, у которых носителями тока являются дырки, имеющие положительный заряд, верхняя грань приобретает в магнитном поле положительный заряд, а нижняя – отрицательный (рис.2, б).
 перемещения зарядов, то сила Лоренца численно будет равна
перемещения зарядов, то сила Лоренца численно будет равна
 , воздействующее на заряды с силой, модуль которой
, воздействующее на заряды с силой, модуль которой
 , поэтому
, поэтому , откуда
, откуда  (1)
(1) ,
, – заряд движущейся частицы,
– заряд движущейся частицы, 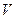 – скорость их упорядоченного движения, получаем
– скорость их упорядоченного движения, получаем

 , будет равна
, будет равна (2)
(2)

 и магнитной индукции
и магнитной индукции  .
. , то проводимость дырочная, если
, то проводимость дырочная, если  , то электронная. Если в полупроводнике одновременно осуществляются оба типа
, то электронная. Если в полупроводнике одновременно осуществляются оба типа

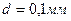 .
. », как показано пунктиром.
», как показано пунктиром. , выведите ручку регулировки выходного напряжения на панели блока БГННП против часовой стрелки до упора.
, выведите ручку регулировки выходного напряжения на панели блока БГННП против часовой стрелки до упора.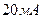 , на «=
, на «= 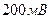 , включите блоки установки выключателями «Сеть» и кнопками мультиметра.
, включите блоки установки выключателями «Сеть» и кнопками мультиметра. в датчике Холла с мультиметра «А» в отчёт:
в датчике Холла с мультиметра «А» в отчёт:
 .
. и запишите значение ЭДС Холла
и запишите значение ЭДС Холла  с мультиметра «
с мультиметра «  . Знак «минус» при записи опустите.
. Знак «минус» при записи опустите.
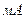




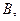

 ,
, сила тока в катушке;
сила тока в катушке; число витков в катушке(
число витков в катушке(  );
);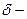 величина зазора(
величина зазора( 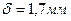 ).
).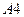 постройте график зависимости
постройте график зависимости  , аппроксимируйте его прямой линией и определите коэффициент наклона по формуле:
, аппроксимируйте его прямой линией и определите коэффициент наклона по формуле:
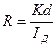 , где
, где толщина пластины полупроводника (
толщина пластины полупроводника ( 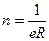 , где
, где величина элементарного заряда (
величина элементарного заряда (  ).
).