 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Погрешности измерения сопротивлений.
ОСНОВЫ ТЕОРИИ Закон Ома для однородного участка цепи. Если на концах однородного участка цепи существует разность потенциалов Dj=j2-j1, то в данной цепи возникает электрический ток. Сила тока I , текущего через данный участок, пропорциональна разности потенциалов Dj на концах участка и обратно пропорциональна сопротивлению R этого участка цепи (или этого проводника)
Величина U = I×R называется падением напряжения на проводнике и численно равна количеству тепла, выделяющегося в проводнике при прохождении через него единичного электрического заряда. Для однородного участка (т.е. не содержащего э.д.с.) разность потенциалов на концах участка численно равна падению напряжения на этом участке, т.е. Dj= U. Если обычный аналоговый вольтметр (отклонение стрелки которого обусловлено током, проходящим в рамке или катушке) присоединить к точкам 1 и 2 участка цепи, то он покажет разность потенциалов Dj между этими точками. Разность потенциалов в этом случае будет равна падению напряжения U на вольтметре, т.е.
где Rv - сопротивление вольтметра, Iv - ток, протекающий через вольтметр. Сопротивление проводников. Если участок цепи представляет собой проводник длиной l постоянного сечения S, однородного химического состава, то сопротивление R этого проводника определяется по формуле:
где r- удельное сопротивление материала. Удельное сопротивление численно равно сопротивление однородного проводника единичной длины и единичного сечения. Оно зависит от химического состава материала проводника, его температуры, и измеряется в системе СИ в Ом×м. На практике часто пользуются внесистемной единицей - Ом×мм2/м При комнатной температуре наименьшее удельное сопротивление имеют проводники из химически чистых металлов. Удельное сопротивление сплавов имеет большую величину, что позволяет применять их для изготовления резисторов с большим сопротивлением (реостаты, нагревательные элементы, шунты и добавочные сопротивления). В табл. 1 даны значения удельного сопротивления некоторых материалов. Таблица 1.
Методы измерения сопротивления. Одним из методов измерения сопротивления проводника является метод "амперметра-вольтметра", состоящим в практическом использовании закона Ома для однородного участка цепи. Из формул (1) и (2) следует
т.е. измеряя разность потенциалов U на концах проводника и величину тока I, протекающего через него, можно определить сопротивление R проводника. Другим методом измерения сопротивлений является метод мостовых схем, который рассматривается в другой лабораторной работе. В мостовых схемах не требуется измерять токи и напряжения, поэтому они дают более точные результаты. Погрешности измерения сопротивлений. При измерениях возникают погрешности, имеющие различную природу. Погрешность метода (или теоретическая погрешность) связана с несовершенством метода, с упрощениями, принятыми в уравнениях для измерений. Погрешность метода проявляется, прежде всего, как систематическая, для компенсации которой возможно введение поправок. При измерении сопротивления методом "амперметра-вольтметра" возникает погрешность, определяемая способом подключения амперметра и вольтметра к исследуемому участку цепи. Для измерения сопротивления R вольтметр и амперметр могут быть включены в цепь по одной из схем, изображенных на рис.1 В схеме 1 а (технический метод с точным измерением тока) вольтметр измеряет разность потенциалов U =j -j на последовательно соединенных проводнике сопротивлением R и амперметре PA сопротивлением RA. Поэтому разность потенциалов, измеренная вольтметром между точками 1 и 2, будет равна сумме падений напряжения на сопротивлении R проводника и сопротивлении RA амперметра:
а б Рис.1 Расчет по формуле (4) будет содержать систематическую погрешность, обусловленную особенностями метода (упрощениями, принятыми при таком расчете). Величина истинного сопротивления R проводника будет равна
где через U обозначена разность потенциалов на участке 1-2. Следовательно, разница DR между результатами измерения сопротивления RЭ по формуле (4) и истинным R и является той методической ошибкой, которая возникает при данном способе включения измерительных приборов.
Относительная погрешность этого метода равна:
Т.е. точность измерения сопротивления будет тем больше, чем меньше сопротивление RA амперметра по сравнению с сопротивлением R проводника. (Идеальным будет амперметр с бесконечно малым собственным сопротивлением). В схеме 1б (технический метод с точным измерением напряжения) амперметром измеряется суммарный ток I , текущий через сопротивление R и вольтметр PV , имеющий собственное сопротивление Rv . Разность потенциалов в этом случае одинакова как для проводника, так и для вольтметра. Тогда по закону Ома (1):
где IR и IV - токи, текущие соответственно через проводник и вольтметр PV , U - разность потенциалов, измеренная вольтметром. Так как измеряемый ток равен I = IR + IV то, учитывая (9), получим
Если не учитывать тока IV , текущего через сопротивление RV вольтметра, то величину сопротивления RЭ проводника также можно найти по упрощенной формуле (4). Величина истинного сопротивления R проводника будет равна
Следовательно, в этом способе измерения также возникает погрешность метода
Относительная погрешность этого метода равна:
т.е. точность измерения сопротивления будет тем больше, чем больше сопротивление вольтметра по сравнению с сопротивлением R проводника Идеальным будет вольтметр с бесконечно большим собственным сопротивлением. Высокоомными являются электронные аналоговые и цифровые вольтметры, вносящие малую погрешность. Погрешности метода возникают при использовании формулы (4). Они могут быть скорректированы, если известны сопротивления амперметра RA или вольтметра RV . Формулы (6) и (10) дают уже исправленный результат измерений, свободный от погрешности этого типа. Другим источником погрешности являются инструментальные погрешности, обусловленные конструкцией прибора. Инструментальные погрешности содержат как систематическую, так и случайную составляющую. При каждом отдельном измерении сопротивления R мы производим измерения тока I и разности потенциалов U с погрешностью, определяемой классом точности измерительного прибора
где gA- класс точности амперметра, имеющего предельный ток Im, gV - класс точности вольтметра с пределом Um. Погрешность определения сопротивления, обусловленная погрешностями приборов определяется по правилам переноса погрешностей косвенных измерений
Из формул (13)-(13') видно, что приборную погрешность можно уменьшить, применяя амперметр и вольтметр высокого класса точности, а также выбирать токи и напряжения такой величины, чтобы стрелки приборов при снятии показаний находились во второй половине шкалы (возможно ближе к пределу измерений). Случайные погрешности возникают при сочетании не воспроизводимых от измерения к измерению факторов: нестабильности источника тока, погрешности оператора, случайной составляющей приборной погрешности и т.д. Для определения случайной погрешности проводят серию многократных измерений Ri при разных токах и напряжениях. Статистическая погрешность DRСТ определяется в соответствии с правилами обработки многократных измерений. Полная погрешность определяется композицией приборной DRПР и статистической DRСТ погрешностей
ОПИСАНИЕ УСТАНОВКИ Прибор FRM-01 представлен на рис.2. К основанию (1) прикреплена колонна (2) с нанесенной миллиметровой шкалой (3). На колонне укреплены два неподвижных кронштейна (4) и один подвижный кронштейн (5), который может передвигаться вдоль колонны и фиксироваться в любом положении. Между верхним и нижним кронштейном натянут нихромовый провод (6).
Рис. 2 Через контактный зажим на подвижном кронштейне обеспечивается хорошее гальваническое соединение с проводом. На подвижном кронштейне нанесена черта, которая облегчает определение по шкале длины отрезка измеряемого нихромового провода. Нижний, верхний и центральный подвижный контакты нихромового провода подведены при помощи проводов низкого сопротивления к измерительной части прибора (7), которая помещена в центральном корпусе. На лицевой панели корпуса расположены амперметр PA, вольтметр PV , клавиша W1 для включения установки в сеть напряжением 220 В, переключатели W2 и W3, ручка реостата R1 регулировки тока. Отжатая клавиша переключателя W3 позволяет использовать нихромовый провод в мостовых схемах измерения сопротивления. Нажатая клавиша W3 позволяет произвести измерение активного сопротивления провода с использованием амперметра и вольтметра. Если клавиша W2 отжата, то измерение происходит по схеме рис.1а - технический метод с точным измерением тока, если нажата- по схеме рис.1б - технический метод с точным измерением напряжения. ВЫПОЛНЕНИЕ РАБОТЫ 1. Заготовьте таблицу результатов измерений. Таблица 2
2. Ручку регулятора тока установите в положение минимального тока (поверните против часовой стрелки до упора). Передвигая подвижный кронштейн (5), установите произвольную длину l проводника. Определите длину проводника, его диаметр (микрометром), класс точности приборов и запишите результаты в табл. 3 Таблица 3 -Справочные данные
3. Включите установку и произведите пять измерений сопротивления при разных токах методом точного измерения тока 4. Заготовьте таблицу, аналогичную табл. 2. Произведите аналогичную серию измерений методом с точным измерением напряжения 5. Выключите установку. ОБРАБОТКА РЕЗУЛЬТАТОВ 1. Вычислите неисправленное RЭi и исправленное значения Ri сопротивления проводника по формулам (4), (6) и (10), а также их средние значения <RЭ> и <R> в каждом методе измерения. 2. Определите погрешности метода em1 и em2 по формулам (8)и (11) для каждого метода измерения. 3. Определите приборные погрешности DRПР и eR для двух опытов по формулам (12)-(13') (для минимального и максимального тока), используя данные более точного метода. 4. Определите случайную погрешность DRСТ и eСТ (для более точного метода). 5. Определите полную абсолютную и относительную погрешности измерения сопротивления DR и eR по формулам (14) и (14'). 6. Определите удельное сопротивление r нихромового провода по формуле (3). 7. Выведите формулу для определения погрешности по правилам оценки погрешностей косвенных измерений (через погрешности DR, Dd, и Dl). Определите абсолютную и относительную Dr погрешности для наиболее точного результата измерений <R>. ВЫВОДЫ 1. Запишите результат измерения R и r в стандартной форме. 2. Какой метод измерения сопротивления точнее? Подтвердите это сравнением погрешностей обоих методов включения амперметра и вольтметра. 3. Какой вид погрешности (метода, приборная или статистическая) имеет наибольшее влияние на результат определения погрешности сопротивления в Ваших опытах? 4. Следует ли учитывать сопротивления амперметра и вольтметра в данных опытах? КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Дайте определение разности потенциалов и падения напряжения на участке цепи. В каком случае они равны? 2. Каков физический смысл сопротивления проводника? От чего оно зависит? 3. В чем состоит метод измерения сопротивления с точным измерением тока? За счет чего возникает погрешность этого метода? Чему она равна, и как ее можно уменьшить? 4. В чем состоит метод измерения сопротивления с точным измерением напряжения? За счет чего возникает погрешность этого метода? Чему она равна, и как ее можно уменьшить? 5. Как определяются приборные и случайные погрешности измерения в данной работе?
ЛИТЕРАТУРА: [1: 34]; [2: 9.1, 9.2]; [3: 98]. |



 (1)
(1) (2)
(2) (3)
(3) (4)
(4) (5)
(5)
 (6)
(6) (7)
(7) (8)
(8) (9)
(9) (9)
(9)
 (10)
(10) (10’)
(10’)
 (11)
(11)

 (12)
(12)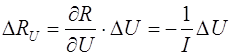 (12’)
(12’) (13)
(13) (13’)
(13’) (14)
(14) (14’)
(14’)