 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Характерные скорости распределения Максвелла
Дополнение к работе № 2 Распределение Максвелла
Движение молекул, совершающих тепловое движение, аналогично движению блуждающей точки. Поэтому
Положим, в (1)α = β, где m –масса молекулы. Тогда выражение (1) примет вид:
где постоянная А определяется из условия нормировки вероятности
Следовательно,
Пользуясь формулой (3), определим среднее значение кинетической энергии молекул:
где учтены значения соответствующих интегралов Пуассона. Таким образом, β характеризует важнейшую величину статистической системы частиц – их среднюю кинетическую энергию. Введем обозначение:
Тогда :
где k – постоянная Больцмана, Т – абсолютная температура, причем в (6)температура введена по определению. С учетом обозначения (5) формула (3) принимает вид:
где φ (νх) является функцией распределения (плотностью вероятности) по проекции скорости νх на ось х. Распределение вероятности движения частиц вдоль осей x, y, z независимы. Для независимых событий по теореме умножения вероятностей имеем:
Переходя от вероятностей к относительному числу частиц, формулу (8) можно представить в ином виде:
где 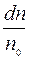 - доля молекул от их общего числа, обладающих вектором скорости в интервале - доля молекул от их общего числа, обладающих вектором скорости в интервале  . Функция . Функция  имеет смысл объемной плоскости вероятности , с которой молекула может оказаться в объеме имеет смысл объемной плоскости вероятности , с которой молекула может оказаться в объеме  пространства скоростей. пространства скоростей. Векторное обозначение аргумента в выражениях (8) и (9) означает, что речь идет о тех молекулах, скорости Вероятность (8) в сферических координатах имеет вид:
Если нас интересует распределение молекул по величине скорости ν, то, используя теорему сложения вероятностей, мы можем интегрировать (10) по углам θ и φ, задающим направление вектора скорости (направление вектора скорости нам безразлично). В результате получим:
Соответствующая функция плотности вероятности имеет вид:
Выражения(8), (9), (12) называются функциями распределения Максвелла по скоростям. Отметим, что в (12) множитель
Характерные скорости распределения Максвелла
1.Величина скорости, при которой функция F(ν) максимальна, называется наиболее вероятной скоростью. Будем обозначать ее через νв. Для нахождения νв нужно продифференцировать функцию F(ν) по аргументу ν и полученный результат приравнять к нулю:
где μ – молярная масса газа. Для воздуха 2.Средняя арифметическая скорость. Пусть при данной температуре газа Δn1 молекул, от общего их числа n, имеют скорость ν1, Δn2 молекул имеют скорость ν2 и т. д. Строго говоря, под Δni надо понимать число молекул, скорости которых лежат в интервале (νi νi + d νi). Составим отношение:
Переходя к пределу, получим значение средней арифметической скорости:
Это же значение можно получить с помощью определения средней величины, а именно: 3.Средняя квадратичная скорость. Определяя средний квадрат скорости по общей формуле, получим:
Из (1), (2), (3) следует, что:
На рисунке3 значение этих скоростей несколько раздвинуты. С увеличением температуры максимум функции распределения F(ν) смещается в сторону больших скоростей, а высота кривой в максимуме несколько понижается.
|



 вероятность того, что тепловая молекула имеет проекцию скорости на ось х в интервале (ν
вероятность того, что тепловая молекула имеет проекцию скорости на ось х в интервале (ν  νх + dνх), будет определяться соотношением:
νх + dνх), будет определяться соотношением: (1)
(1) (2)
(2)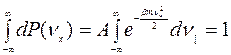 =>
=> 
 (3)
(3) (4)
(4) (5)
(5) (6)
(6) (7)
(7)
 (8)
(8) (9)
(9)
 которых на рис.1 изображаются векторами с концами внутри данного объема
которых на рис.1 изображаются векторами с концами внутри данного объема  пространства скоростей.
пространства скоростей. (10)
(10) (11)
(11) (12)
(12) при возрастании ν убывает быстрее, чем растет множитель ν2 и функция F(ν), начинаясь в нуле (из-за множителя ν2), достигает максимума и затем асимптотически стремится к нулю. Этим объясняется асимметрия графика функции F(ν) (рис.2).Отметим также, что вид кривой F(ν) зависит от массы молекулы и температуры газа. Однако площади, ограниченные каждой кривой F(v,m,T) b и осью скоростей, должны, по условию нормировки, оставаться одинаковыми при любой температуре и для любого газа.
при возрастании ν убывает быстрее, чем растет множитель ν2 и функция F(ν), начинаясь в нуле (из-за множителя ν2), достигает максимума и затем асимптотически стремится к нулю. Этим объясняется асимметрия графика функции F(ν) (рис.2).Отметим также, что вид кривой F(ν) зависит от массы молекулы и температуры газа. Однако площади, ограниченные каждой кривой F(v,m,T) b и осью скоростей, должны, по условию нормировки, оставаться одинаковыми при любой температуре и для любого газа. (1)
(1) при температуре Т= 273К, νв=400м/с.
при температуре Т= 273К, νв=400м/с.
 (2)
(2) , где учтены значения соответствующих интегралов Пуассона.
, где учтены значения соответствующих интегралов Пуассона.
 (3)
(3)