ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Анализ качества и прогнозирование модели временных рядов
ЛАБОРАТОРНАЯ РАБОТА №4
1. Производим сглаживание временного ряда. Представим таблицу исходных данных для удобства расчетов следующим образом.
В качестве скользящей средней выберем простое среднее арифметическое по трем последовательным уровням временного ряда. 2. Определяем вид модели временного ряда (аддитивная или мультипликативная). Дополним расчетную таблицу столбцом «Циклическая составляющая». Так как циклическая составляющая имеет периодический характер изменения своего значения, то выбираем аддитивную модель временного ряда. 3. Выделим и устраним сезонные колебания из временного ряда. В нашей задаче сезонность будем рассматривать годовую и понимать как го-довую специфику изменения фактора риска.. Дополним расчетную таблицу столбцом «Абсолютное отклонение в сезоне (оценки сезонных колебаний)». Вычисляем абсолютное отклонение по каждому году, усредняя циклическую состав-ляющую, то есть получаем оценку сезонной составляющей по соответствующему году.
Проверим выполнимость требований к сезонным составляющим для аддитивной модели: сумма всех сезонных компонент должна быть равна нулю. Сумма равна 0,294,то есть не равна 0. Так как требование к сезонным составляющим не выполняется, то рассматривать будем исправленное абсолютное отклонение по каждому году. Для этого дополним расчетную таблицу еще одним столбцом «Исправленное абсолютное отклонение в сезоне (оценки сезонных колебаний)». Таким образом, в столбце 8 получили оценки сезонных составляющих с учетом требований к ним. Дополним расчетную таблицу столбцом «Ряд с удаленной сезонной компонентой (У)». Удалять сезонную составляющую будем, вычитая из уровней исходного временного ряда соответствующую оценку сезонной составляющей. 4. Определим вид функции тренда. Дополним расчетную таблицу столбцами: «Конечные разности первого порядка», «Конечные разности второго порядка» и «Темпы прироста».
Сравнивая столбцы 10 – 12 можно сказать, что темпы прироста наиболее постоянны, следовательно, тенденцию лучше выражать показательной регрессией.
5. Оценим параметры тренда и устраним последний из временного ряда. Произведем линеаризацию уравнения тренда, переписав предварительно его в виде:
Произведем следующую замену:
Получили уравнение парной линейной регрессии, параметры которой нужно оценить:
Составим соответствующую систему нормальных уравнений для модели парной линейной регрессии, из которой найдем оценки параметров:
Получаем оценку параметров исходного уравнения тренда:
Дополним расчетную таблицу еще тремя столбцами: « Вычислим средние значения
Вычисляем оценки параметров
Вычисляем оценки параметров
Записываем уравнение тенденции
Получим ряд остатков, удаляя значения тренда из исходного временного ряда. Получив ряд остатков временного ряда, можно произвести анализ качества построенной модели временного ряда, а в отношении исходного временного ряда можно сказать, что он стал стационарным и представляет теперь ряд остатков временного ряда. 6. Произведем анализ качества построенной модели временного ряда. Проверяем условие случайности возникновения отдельных отклонений от тренда. Дополним расчетную таблицу столбцом «Повторные точки».
Определяем, какие уровни ряда остатков являются повторными точками. Определим количество повторных точек в ряде остатков. Оно равно 9. Определяем критическое значение Р для критерия случайности отклонений от тренда.
Так как 6<8, то ряд остатков нельзя считать случайным, то есть он содержит детерминированную составляющую. В таком случае либо необходимо строить новую модель, либо пренебречь этим условием и проверить остальные условия, характеризующие качество построенной модели. Проверим равенство математического ожидания уровней ряда остатков нулю. Вычисляем среднее значение ряда остатков.
Вычисляем стандартную ошибку отклонения от тренда.
Проверяем гипотезы:
Строим статистику:
Находим квантиль распределения Стьюдента с (T-1) степенью свободы при уровне значимости, равном 0,05, где T– объем выборки.
Делаем вывод о принятии гипотезы Гипотеза отвергается и принимается альтернативная гипотеза, следовательно, математическое ожидание случайной составляющей не равно нулю. Проверим нормальность распределения уровней ряда остатков по RS-критерию. Проверяем гипотезы:
Строим статистику:
Определяем критические границы RS-критерия:
Делаем вывод о принятии гипотезы:
принимается, то есть ряд остатков нормален. Допуская неслучайность уровней ряда остатков, можно считать, что построенная модель временного ряда качественная, то есть она адекватно описывает исходные данные.
7. Осуществим точечный прогноз объема товарооборота на первый квартал 2013 года по построенной модели, подставив номер квартала в уравнение тренда и определив значение зависимой переменной
Фактор риска на первый квартал 2013 года составит 14,041. 8. Дадим графическую интерпретацию построенной модели временного ряда, изобразив на одной плоскости оценку тренда, исходный временной ряд и ряд, очищенный от влияния цикличности и сезонности.
|









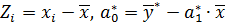


 », «Оценка тренда» и «Ряд остатков».
», «Оценка тренда» и «Ряд остатков». :
: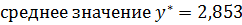

 и
и 
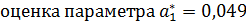

 ,
, 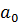




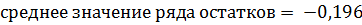










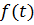 .
.