 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Делимость суммы, разности, произведения целых неотрицательных чисел
Лекция 4. Делимость на множестве целых неотрицательных чисел 1. Понятие отношения делимости, его свойства. 2. Признаки делимости суммы, разности, произведения. 3. Признаки делимости на 2, 3, 4, 5, 9 (два доказать).
В начальном курсе математики делимость натуральных чисел, как правило, не изучается, но многие факты из этого раздела математики неявно используются. Отношение делимости и его свойства Рассмотрим отношение делимости на множестве целых неотрицательных чисел. Определение 1. Пусть даны целые неотрицательные числа а и b. Говорят, что число а делится на натуральное число b, если существует такое целое неотрицательное число q, что а=bq. В этом случае число b называют делителем числа а, а число а - кратным числа b. Обознаение: а Заметим, что понятие "делитель данного числа" следует отличать от понятия "делитель", обозначающего то число, на которое делят. Например, если 18 делят на 5, то число 5 - делитель, но не является делителем числа 18. Если 18 делят на 6, то в этом случае понятия "делитель" и "делитель данного числа" совпадают. Замечание. Из определения 1 и равенства а=1а, следует, что 1 является делителем любого целого неотрицательного числа. Свойства отношения делимости: Отношение делимости рефлексивно, антисимметрично, транзитивно. Теорема 1. Отношение делимости рефлексивно, т.е. любое натуральное число делится само на себя Доказательство: Для Теорема 2. Отношение делимости антисимметрично, т. е.
Доказательство (методом от противного): Предположим, что Теорема 3. Отношение делимости транзитивно, то есть
Доказательство: Т.к. Тогда a=bq=(cp)q=c(pq). Число рq- натуральное. Это означает по опр.1, что а Таким образом, отношение делимости на множестве N, обладая свойствами рефлексивности, антисимметричности и транзитивности, является отношением нестрогого порядка. Делимость суммы, разности, произведения целых неотрицательных чисел Теорема 4 (признак делимости суммы):Если каждое слагаемое суммы делится на натуральное число b, то и вся сумма делится на это число, то есть если Доказательство: Пусть Теорема 5 (признак делимости разности): Если каждое из чисел а и b делится на с и а≥b, то разность а-b делится на с, т. е. если Доказательство: Пусть Теорема 6 (признак делимости произведения): Если хотя бы один из множителей произведения делится на натуральное число b, то и все произведение делится на это число, то есть Доказательство: Пусть аk Теорема 7: Если в произведении ab множитель а делится на натуральное число m, а множитель b делится на натуральное число n, то произведение ab делится на произведение nm, то есть Доказательство: Пусть a Теорема 8: Если в сумме одно слагаемое не делится на натуральное число b, а все остальные слагаемые делятся на это число, то и вся сумма на число b не делится. Доказательство: Пусть S=a1+a2+…+an+c, где а1 Признаки делимости Теорема 9 (признак делимости на 2) Для того чтобы число х делилось на 2, необходимо и достаточно, чтобы его десятичная запись оканчивалась одной из цифр 0,2,4,6,8. Доказательство. Пусть число х записано в десятичной системе счисления, т.е. х = аn·10 + аn-1·10n-1 + ... + а 1·10 + а0, где аn, аn-1,…,a1 принимают значения 0, 1, 2, ...9, аn ≠0 и а 0 принимает значения 0,2,4,6,8. Докажем, что тогда х :.2. Так как 10:.2, то 102 :.2, 103 :.2,…,10 n :.2 и, значит, (аn·10 + аn-1·10n-1 + ... + а1·10) :.2. По условию а0 тоже делится на 2, поэтому число х можно рассматривать как сумму двух слагаемых, каждое из которых делится на 2. Следовательно, согласно признаку делимости суммы, число хделится на 2. Докажем обратное: если число х делится на 2, то его десятичная запись оканчивается одной из цифр 0,2,4,6,8. Запишем равенство х = аn·10 + аn-1·10n-1 + ... + а 1·10 + а0 в таком виде: а0 = х - ( аn·10 + аn-1·10n-1 + ... + а 1·10 ). Но тогда, по теореме о делимости разности, а0 : . 2, поскольку х : . 2 и (аn·10 + аn-1·10n-1 + ... + а 1·10) :. 2. Чтобы однозначное число а0 делилось на 2, оно должно принимать значения 0,2,4,6,8. Теорема 10 (признак делимости на 5). Для того чтобы число х делилось на 5, необходимо и достаточно, чтобы его десятичная запись оканчивалась цифрой 0 или 5. Доказать самостоятельно! Доказательство этого признака аналогично доказательству признака делимости на 2. Теорема 11 (признак делимости на 4). Для того чтобы число х делилось на 4, необходимо и достаточно, чтобы на 4 делилось двузначное число, образованное последними двумя цифрами десятичной записи числа х. Доказательство. Пусть число х записано в десятичной системе счисления, т.е. х = аn·10 + аn-1·10n-1 + ... + а 1·10 + а0 и последние цифры в этой записи образуют число, которое делится на 4. Докажем, что тогда х: . 4. Так как 100:. 4, то (аn·10 + аn-1·10n-1 + ... + а 2·102) :. 4. По условию, а 1 ·10 + а0 (это и есть запись двузначного числа) также делится на 4. Поэтому число х можно рассматривать как сумму двух слагаемых, каждое из которых делится на 4. Следовательно, согласно признаку делимости суммы, и само число х делится на 4. Докажем обратное, т.е. если число х делится на 4, тo двузначное число, образованное последними цифрами его десятичной записи, тоже делится на 4. Запишем равенство х = аn·10 + аn-1·10n-1 + ... + а 1·10 + а0 в таком виде: а1·10 + а0 = х- (аn·10 + аn-1·10n-1 + ... + а 2·102). Так как х :. 4 и (аn·10 + аn-1·10n-1 + ... + а 2·102) : . 4, то по теореме о делимости разности (а1·10 + а0) :. 4. Но выражение а1·10 + а0 есть запись двузначного числа, образованного последними цифрами записи числа х. Теорема12 (признак делимости на 9)Для того чтобы число х делилось на 9, необходимо и достаточно, чтобы сумма цифр его десятичной записи делилось на 9. Доказательство. Докажем сначала, что числа вида 10n - 1 делятся на 9. Действительно, 10n - 1 = (9·10n-1 + 10n-1) - 1 = (9·10n-1 +9·10n-2+ 10n-2)-1 = (9·10n-1 +9·10n-2+ …+10)-1=9·10n-1 +9·10n-2+ …+9. Каждое слагаемое полученной суммы делится на 9, значит, и число 10n- 1 делится на 9. Пусть число х = аn·10 + аn-1·10n-1 + ... + а1·10 + а0 и (a n +a n-1 +…+a 1 +a 0 ):. 9. Докажем, что тогда х:. 9. Преобразуем сумму аn·10 + аn-1·10n-1 + ... + а1·10 + а0, прибавив и вычтя из нее выражение a n +a n-1 +…+a 1 +a 0 и записав результат в таком виде: х = (аn·10 - a n )+( аn-1·10n-1 - a n-1 )+…+( а1·10 - a 1 )+ (а0 – а 0 )+ (a n+a n-1 +…+a 1 +a 0 )= =аn·(10n -1)+ a n-1 ·(10n-1 -1)+…+ a 1·(10 -1)+ (a n +a n-1 +…+a 1 +a 0 ). В последней сумме каждое слагаемое делится на 9: аn·(10n -1) :. 9, так как (10n -1) :. 9, a n-1 ·(10n-1 -1) :. 9,так как(10n-1 -1) :. 9 и т.д. a 1·(10 -1) :. 9, так как (10- 1) :. 9, (a n +a n-1 +…+a 1 +a 0 ) :. 9 по условию. Следовательно, х:. 9. Докажем обратное, т.е. если х:. 9, то сумма цифр его десятичной записи делится на 9. Равенство х = аn·10 + аn-1·10n-1 + ... + а 1·10 + а0 запишем в таком виде: a n +a n-1 +…+a 1 +a 0 = х - (аn(10n - 1) + аn-1·(10n-1 -1) +…+ a 1·(10 -1). Так как в правой части этого равенства и уменьшаемое, и вычитаемое кратны 9, то по теореме о делимости разности (a n +a n-1 +…+a 1 +a 0 ) :. 9, т.е. сумма цифр десятичной записи числа x делится на 9, что и требовалось доказать. Теорема15 (признак делимости на 3):Для того чтобы число х делилось на 3, необходимо и достаточно, чтобы сумма цифр его десятичной записи делилась на 3. Доказательство этого утверждения аналогично доказательству признака делимости на 9.
|



 b и говорят а кратно b, а b называют делителем числа а.
b и говорят а кратно b, а b называют делителем числа а. .
. справедливо равенство а=а•1. Т.к. 1
справедливо равенство а=а•1. Т.к. 1  , то по опр. 1
, то по опр. 1  .
. .
.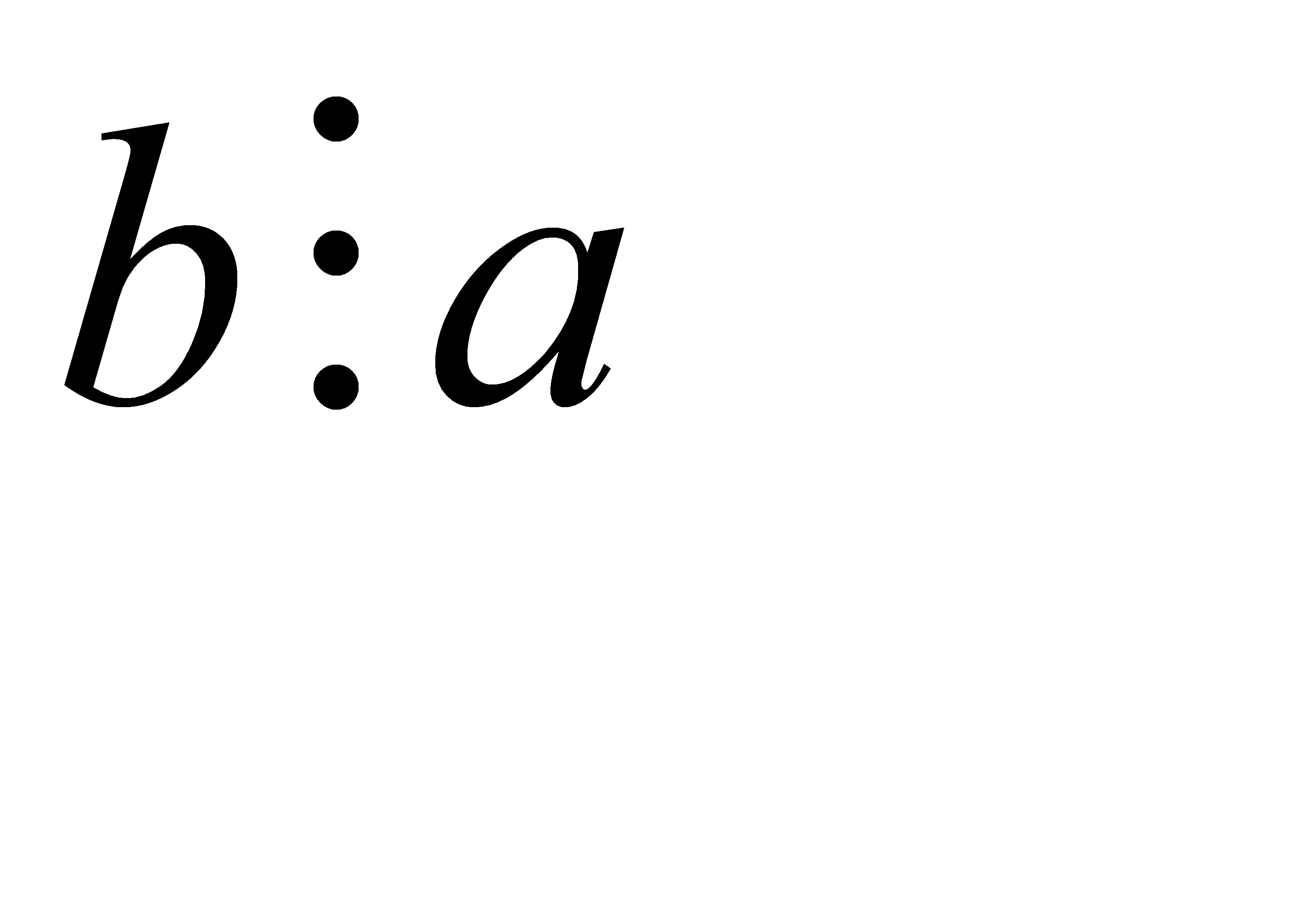 . Тогда очевидно, что b≥a. Но по условию
. Тогда очевидно, что b≥a. Но по условию  и значит а≥b. Выполнение этих неравенств возможно только при а=b, что противоречит условию. Следовательно, наше предположение неверно и справедливость свойства установлена.
и значит а≥b. Выполнение этих неравенств возможно только при а=b, что противоречит условию. Следовательно, наше предположение неверно и справедливость свойства установлена. .
. . Аналогично, т.к. b
. Аналогично, т.к. b  .
.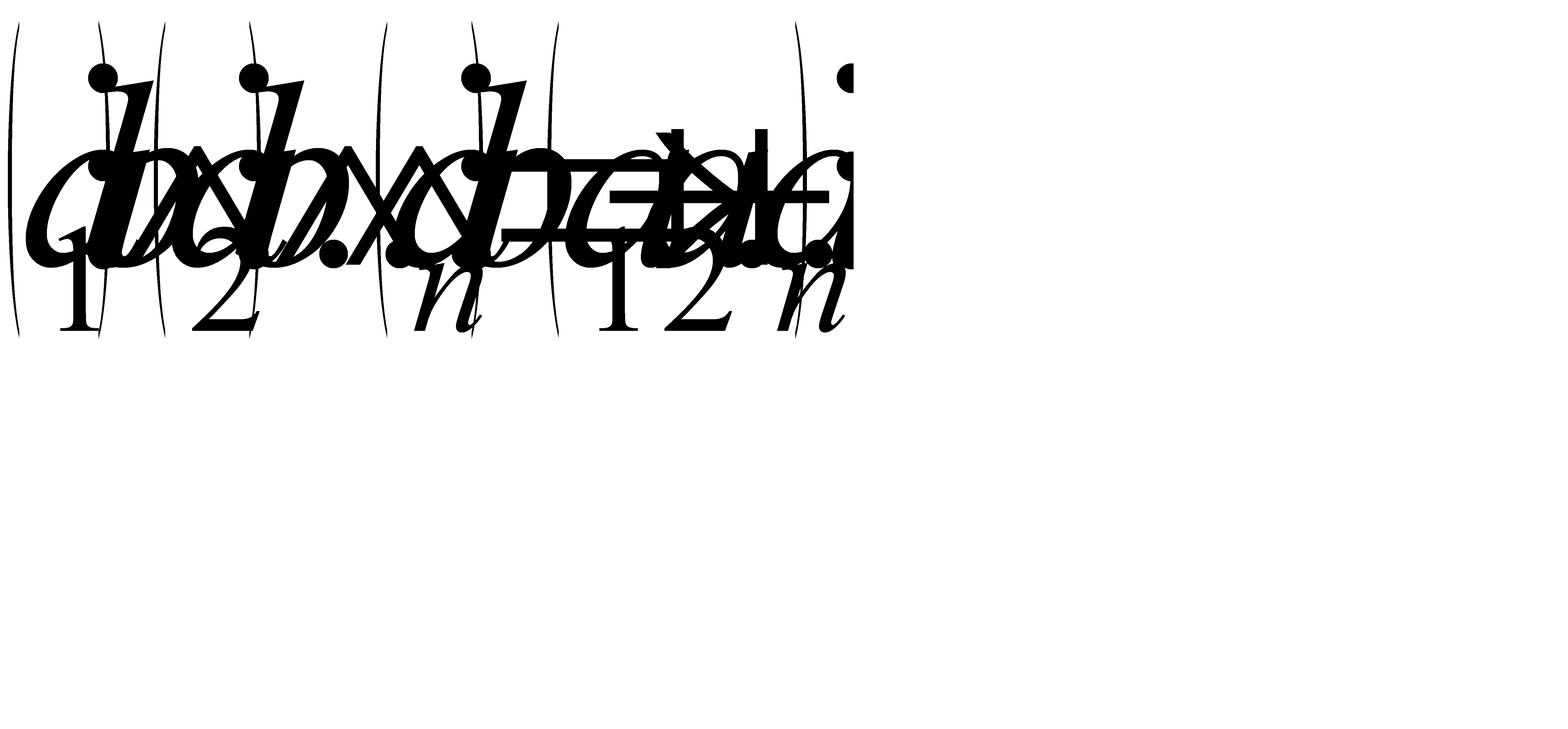 .
. . Тогда существуют q1,q2,…qn
. Тогда существуют q1,q2,…qn  N такие, что выполняются равенства: а1=bq1, а2=bq2, …, а1n=bqn. Из этих равенств следует, что а1+а2+…аn=bq1+bq2+…+bqn=b(q1+q2+…+qn), где q1+q2+…+qn=q
N такие, что выполняются равенства: а1=bq1, а2=bq2, …, а1n=bqn. Из этих равенств следует, что а1+а2+…аn=bq1+bq2+…+bqn=b(q1+q2+…+qn), где q1+q2+…+qn=q  .
. .
. . Тогда существуют q1,q2
. Тогда существуют q1,q2  .
. .
. . Поскольку произведение целых неотрицательных чисел является целым неотрицательным числом, то последнее равенство означает, что
. Поскольку произведение целых неотрицательных чисел является целым неотрицательным числом, то последнее равенство означает, что  .
. .
. . Докажем, что
. Докажем, что  . Предположим противное, то есть S
. Предположим противное, то есть S