 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Электродвижущая сила и электромагнитный момент машины постоянного тока
Электродвижущая сила. Она наводится в обмотке якоря основным магнитным потоком. Исходной формулой для получения выражения электродвижущей силы обмотки якоря является формула закона электромагнитной индукции
Е = Blvsinα
Если применить ряд упрощений, например, заменим действительное распределение индукции в зазоре прямоугольным (график 2), при этом высоту прямоугольника примем равной максимальному значению индукции Величина bm длина полюсной дуги(внутренняя дуга полюсного наконечника) Величина bi называется расчетной полюсной дугой. αi=
αi - коэффициент полюсного перекрытия
τ - полюсное деление В машинах постоянного тока расчетная полюсная дуга мало отличается от полюсной дуги
Воспользовавшись коэффициентом полюсного перекрытия
получим
Коэффициент полюсного перекрытия Обычно
При выводе формулы ЭДС будем исходить из прямоугольного закона распределения индукции в зазоре, при этом магнитная индукция на участке расчетной полюсной дуги А также приняв ряд других упрощений, получим выражение ЭДС машины постоянного тока (В):
(4.13)
Рис. 4.9. Распределение магнитной индукции в воздушном зазоре машины постоянного тока
В системе СИ формула 4.13 примет вид
где
Еа - ЭДС машины постоянного тока се - постоянная для данной машины величина; k - постоянная для данной машины величина в системе СИ Ф — основной магнитный поток, Вб;
ω - частота вращения якоря, рад/с; р - число пар полюсов обмотки якоря; N - число пазовых сторон обмотки якоря; а - число пар параллельных ветвей обмотки якоря;
Электромагнитный момент.
При прохождении по пазовым проводникам обмотки якоря тока
Совокупность всех электромагнитных сил Можно получить формулу для определения электромагнитного момента М обмотки якоря
(4.15) или в системе СИ
где
М - электромагнитный момент машины постоянного тока, Н/м (ньютон делить на метр) см - постоянная для данной машины величина; Ф — основной магнитный поток, Вб (вебер) р - число пар полюсов обмотки якоря N - число пазовых сторон обмотки якоря а - число пар параллельных ветвей обмотки якоря
Электромагнитный момент машины при ее работе в двигательном режиме является вращающим, а при генераторном режиме — тормозящим по отношению к вращающему моменту приводного двигателя.
Подставив из (4.13) в (4.15) выражение основного магнитного потока
М = Рэм/ω
где
Рэм— электромагнитная мощность машины постоянного тока,Вт.
Из (4.16) следует, что в машинах равной мощности электромагнитный момент больше у машины с меньшей частотой вращения якоря.
|



 , а ширину — равной величине
, а ширину — равной величине  , при которой площадь прямоугольника равна площади, ограниченной криволинейной трапецией.
, при которой площадь прямоугольника равна площади, ограниченной криволинейной трапецией. , где (4,10)
, где (4,10) :
: , (4.11)
, (4.11) ,
, (4.12)
(4.12) имеет большое влияние на свойства машины постоянного тока. На первый взгляд кажется целесообразным выбрать наибольшее значение
имеет большое влияние на свойства машины постоянного тока. На первый взгляд кажется целесообразным выбрать наибольшее значение  равна
равна  се =
се = 

 Фω=kФω
Фω=kФω 
 — частота вращения якоря, об/мин;
— частота вращения якоря, об/мин; на каждом из проводников появляется электромагнитная сила, которая определяется по закону Ампера
на каждом из проводников появляется электромагнитная сила, которая определяется по закону Ампера . (4.14)
. (4.14) на якоре, действующих на плечо, равное радиусу сердечника якоря
на якоре, действующих на плечо, равное радиусу сердечника якоря  , создает на якоре электромагнитный момент М.
, создает на якоре электромагнитный момент М.

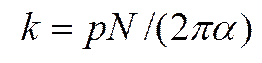
 — ток якоря, А;
— ток якоря, А; , получим еще одно выражение электромагнитного момента:
, получим еще одно выражение электромагнитного момента: , (4.16)
, (4.16) — угловая скорость вращения;
— угловая скорость вращения; (4.17)
(4.17)