ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

Описание опытного устройства

12 3

ЛАБОРАТОРНЫЙ ПРАКТИКУМ НА ПОРТАТИВНОЙ УСТАНОВКЕ «КАПЕЛЬКА»

ЛАБОРАТОРНАЯ РАБОТА № 3

ИЛЛЮСТРАЦИЯ УРАВНЕНИЯ БЕРНУЛЛИ. ПОСТРОЕНИЕ ЛИНИЙ ЭНЕРГИИ И ПОТЕНЦИАЛЬНОЙ ЭНЕРГИИ

Общие сведения

Закон сохранения энергии в гидравлике выражается уравнением Бернулли. Для струйки невязкой жидкости оно имеет вид

, (1)

где z – нивелирная высота, м;

p – давление, Па;

ρ – плотность, кг/м³;

g – ускорение свободного падения, м/с²;

u – скорость, м/с.

При движении вязкой жидкости имеют место потери на трение h_1-2. Для потока вязкой жидкости уравнение Бернулли имеет вид

(2)

Индексы «1» и «2» указывают на номер сечения, к которому относится величина.

Слагаемые уравнения выражают энергии, приходящиеся на единицу веса (силы тяжести) жидкости, которые в гидравлике принято называть напорами

– пьезометрический напор (потенциальная энергия),

– скоростной напор (кинетическая энергия),

– полный (гидродинамический) напор (полная механическая энергия жидкости),

h_1-2 – потери напора (потери механической энергии за счет ее преобразования в тепловую энергию). Такие энергии измеряются в единицах длины/

Через гидродинамический напор уравнение Бернулли имеет вид

H₀₁-H₀₂=h_1-2 (3)

В формуле (2) v означает среднюю скорость, а коэффициент Кориолиса α учитывает распределение скоростей в живом сечении. Если мы соединим уровни жидкости в пьезометрах (рис. 2), то получим линию потенциальной энергии, показывающую изменение потенциальной энергии потока относительно плоскости сравнения. Соединив гидродинамические напоры в разных сечениях, получим линию энергии. Энергия h_1-2 превращается в тепло и рассеивается в пространстве. Процесс превращения механической энергии в тепловую с последующим рассеиванием в пространстве называется диссипацией. Диссипация – процесс необратимый.

Потеря энергии на единицу длины называется гидродинамическим уклоном

(4)

Изменение потенциальной энергии характеризуется пьезометрическим уклоном

. (5)

Гидравлический уклон всегда положителен и равен тангенсу угла наклона между касательной к линии энергии в рассматриваемом сечении и обратным направлением движения.

В то же время давление вдоль движения может уменьшаться или увеличиваться (при увеличении или уменьшении скорости), вследствие чего пьезометрический уклон может быть и положительным и отрицательным.

Цель работы

Визуально наблюдать переход энергии из потенциальной в кинетическую и обратно.

Построить линии энергии и потенциальной энергии для трубопровода переменного сечения.

Описание опытного устройства

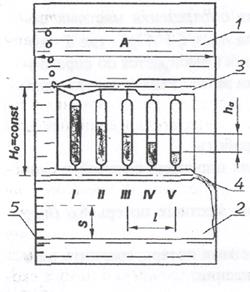
Устройство содержит баки 1 и 2, сообщаемые через каналы переменного 3 и постоянного 4 сечений (рис. 1). Каналы соединены между собой равномерно расположенными пьезометрами I-V, служащими для измерения пьезометрических напоров в характерных сечениях. Устройство заполнено подкрашенной водой. В одном из баков предусмотрена шкала 5 для измерения уровня воды. При перевертывании устройства благодаря постоянству напора истечения Н_о во времени обеспечивается установившееся движение воды в нижнем канале. Другой канал в это время пропускает воздух, вытесняемый жидкостью из нижнего бака в верхний.

Рис.1. Опытное устройство: 1,2 - баки; 3,4 — каналы переменного и постоянного сечения; 5 - уровнемерная шкала; I-V – пьезометры

Порядок выполнения работы

1. При заполненном водой баке 2 (рисунок 1) перевернуть устройство для получения течения в канале переменного сечения 3.

2. Снять показания пьезометров Н=p/(ρg) по нижним частям менисков воды в них.

3. Измерить время t перемещения уровня в баке на произвольно заданную величину S.

4. По размерам А и В поперечного сечения бака, перемещению уровня S и времени t определить расход Q воды в канале, а затем скоростные и полные напоры в сечениях канала по порядку, указанному в таблице 1.

Таблица 1 – Исходные данные

Наименование величин	Обозначения, формулы	Сечения канала
I	II	III	IV	V	VI
1. Площадь сечения канала, см	ω
2. Средняя скорость, см/с
3. Пьезометрический напор, см
4. Скоростной напор, см
5. Полный напор, см

ПримечаниеА =... см; B =... см; S=... см; t =... с; Q = ABS/t =... см³/с

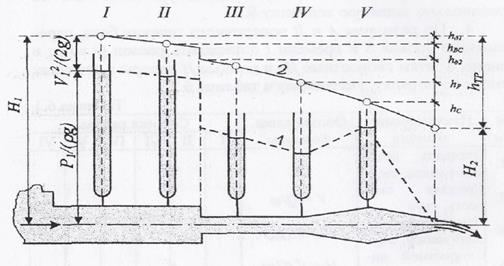
5. Вычертить в масштабе канал с пьезометрами (рисунок 2). Соединив уровни жидкости в пьезометрах и центром выходного сечения VI, получить пьезометрическую линию 1, показывающую изменение потенциальной энергии (давления) вдоль потока. Для получения напорной линии 2 (линии полной механической энергии) отложить от оси канала полные напоры H и соединить полученные точки.

6. Проанализировать изменение полной механической H, потенциальной и кинетической энергий жидкости вдоль потока; выяснить соответствие этих изменений уравнению Бернулли.

Рисунок 2 – . Иллюстрация уравнения Бернулли:

1,2 – пьезометрическая и напорная линии;

Н₁, Н₂ – полные напоры (механические энергии) на входе и выходе из канала;

h_ТР, h_δ₁, h_δ₂,, h_BC, h_Р, h_С – потери напора: суммарные, по длине на 1 и 2 участках, на внезапное сужение, на плавные расширения и сужения

Содержание отчета

1. Записать цель работы.

2. Нарисовать схему лабораторной установки.

3. Выписать расчетные формулы.

4. Заполнить таблицу с данными наблюдений и результатами расчетов.

5. Нанести линии энергии и потенциальной энергии.

6. Проанализировать изменение полной, потенциальной и кинетической

энергии и сделать вывод.

Вопросы для самопроверки

1. В чем заключается геометрический и энергетический смысл уравнения Бернулли?

2. Чем вызваны потери энергии при движении вязкой жидкости по трубопроводу?

3. Что такое диссипация энергии?

4. Что такое гидравлический уклон и от чего он зависит?

5. Что такое гидродинамический напор?

6. Как определяется средняя скорость потока?

7. О чем говорит коэффициент Кориолиса?

8. Написать уравнение сплошности потока.

9. Указать на графике скоростной напор в любом сечении.

10. Как по графику линий энергии и потенциальной энергии определить гидравлический (пьезометрический) уклон в заданном сечении?

11. В каком сечении будет наименьшая пьезометрическая высота?

ЛАБОРАТОРНАЯ РАБОТА №4

12 3