ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| МЕТОД ОПРЕДЕЛЕНИЯ ТЕПЛОЁМКОСТИ ТВЁРДОГО ТЕЛА
ФГБОУ ВПО «КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» КАФЕДРА ФИЗИКИ ЛАБОРАТОРНАЯ РАБОТА № 303 ОПРЕДЕЛЕНИЕ ТЕПЛОЁМКОСТИ МЕТАЛЛОВ МЕТОДОМ ОХЛАЖДЕНИЯ Методическое указание к выполнению лабораторной работы по разделу «Молекулярная физика» для студентов всех форм обучения по всем специальностям
Калининград ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Различные тела, обладающие одной и той же массой, нагреваются по-разному при сообщении им одного и того же количества тепла. Говорят, что они различаются теплоёмкостью. Теплоёмкостью (истинной) С тела называется отношение элементарного количества тепла dQ, сообщённого телу в каком-либо процессе, к соответствующему изменению температуры тела:
Примечание. Поскольку теплота (как и работа) является функцией процесса изменения состояния системы, то элементарное количество тепла не является полным дифференциалом, что и нашло своё отражение в обозначениях этой формулы (δQ, а не dQ). Средней Сср теплоёмкостью тела в интервале температур от Т1 до Т2>Т1 называется отношение количества тепла Q, необходимого для повышения температуры тела, к разности этих температур:
Сср = Связь между средней и истинной теплоёмкостями тела имеет вид:
Теплоёмкость зависит от массы тела, его химического состава, термодинамического состояния и вида процесса сообщения тепла. Теплоёмкость можно отнести к единице массы, к одному молю и к единице объёма тела. Соответственно этому теплоёмкость называется удельной, молярной, объёмной. Единицами измерения теплоёмкости в системе СИ являются Дж / град и внесистемная единица кал / град или ккал / град. Удельную, молярную и объёмную теплоёмкости в системе СИ измеряют соответственно в Дж / кг·град, Дж / моль·град и Дж/ /м3 ·град. Внесистемными единицами являются кал / кг·град, кал / моль·град, кал / м3·град или ккал / кг·град, ккал / моль·град, ккал / м3·град. Поскольку количество тепла является функцией процесса, то значение теплоёмкости зависит от условий теплопередачи. Однако, если условия теплопередачи фиксированы, то теплоёмкость выражается через функцию состояния тела. Так, для газов, в зависимости от характера термодинамического процесса, различают теплоёмкость при постоянном объёме Сv и теплоёмкость при постоянном давлении Сp . В первом случае нагревание (или охлаждение) осуществляется при неизменном объёме газа, во втором случае поддерживается постоянное давление. Теплоёмкость тела характеризует его способность изменять свою внутреннюю энергию при сообщении телу теплоты. Теплоёмкость твёрдого тела связана с энергией атомов, совершающих колебания вокруг своих положений равновесия. При достаточно высокой температуре эти колебания можно рассматривать с помощью классической механики. Молекула, находясь в поступательном колебательном движении, обладает тремя степенями свободы. На каждую степень свободы приходится средняя кинетическая энергия Находясь в колебательном движении, молекула обладает также потенциальной энергией. Причём, в этом случае среднее значение по- тенциальной энергии равно среднему значению кинетической энергии. Следовательно, на каждую из трёх степеней свободы атома приходится средняя энергия кТ (сумма средней потенциальной и средней кинетической энергии).
<W> = kT (1)
Умножив kT на З (число степеней свободы), получим среднюю энергию, приходящуюся на один атом твёрдого тела. Этот предел, однако, для сколько-нибудь сложных соединений никогда не достигается, так как вещество уже раньше плавится или разлагается. Для многих простых элементов этот предел достигается при обычных температурах. Полную энергию одного моля твёрдого тела получим, если умножим среднюю энергию одной частицы на число независимо колеблющихся частиц, содержащихся в одном моле. Это число равно числу Авогадро NA = 6,02 · 1026 кмоль-1
U = 3NA < W> (2)
U = 3NA kT = 3RT, (З)
где R — универсальная газовая постоянная. Отсюда атомная (молярная) теплоёмкость будет равна: Cm = Этот результат находится в согласии с экспериментально установленным в I8I9 г. законом (правилом) П.Дюлонга и А.Пти: Молярная теплоёмкость всех химически простых кристаллических твёрдых тел приблизительно равна 6 Закон Дюлонга и Пти сравнительно хорошо подтверждается на опыте при не слишком низких температурах. Из рис.1 видно, что для многих веществ это правило соблюдается уже при температуре 0 °С. Многочисленные опыты по определению теплоёмкости большого числа кристаллических твёрдых тел в широком диапазоне температур показали, что результаты, выражаемые формулами (3) и (4), являются весьма приближёнными, а в некоторых случаях просто неверными. Из формул (3) и (4) следует, что молярная теплоёмкость не зависит ни от температуры, ни от конкретных свойств кристаллов. Опыты же показали, что в действительности такая зависимость существует, причём особенно резко она проявляется при низких температурах (см. рис.1).
0 100 200 300 400 500 600 Т, К Рис.1.
При достаточно низких температурах теплоёмкость всех твёрдых
Таким образом, при абсолютной температуре, стремящейся к нулю, теплоёмкость твёрдых тел также стремится к нулю. Теплоёмкость некоторых тел, например, алмаза и бора, весьма заметно зависит от температуры даже при сравнительно высоких температурах. Причина расхождения классической теории теплоёмкостей твёрдых тел с опытами состоит в ограниченной применимости закона равномерного распределения энергии по степеням свободы. Ведь именно этот закон приводит к формулам (3), (4) и, следовательно, к независимости теплоёмкости твёрдых тел от температуры. Трудности классической теории теплоёмкости твёрдых тел были преодолены в современной квантовой теории. Первоначально квантовая теория теплоёмкости твёрдых тел была развита А.Эйнштейном в 1905 г. В её основе лежало предположение о том, что каждый атом, колеблющийся в узле кристаллической решётки, имеет три степени свободы, причём в кристалле, построенном из частиц одного сорта, все атомы колеблются независимо друг от друга с одинаковой частотой. Кроме этого, А.Эйнштейн предположил, что энергия атома, гармонически колеблющегося в узле решётки с частотой n, может принимать не любые, а только вполне определённые значения, кратные величине кванта энергии hn, где h = 6,625·10-34 Дж·с - постоянная Планка. Энергия, приходящаяся на одну степень свободы, принимает значения: W = n·h· Впоследствии выяснилось, что необходимо принимать во внимание так называемую нулевую энергию Задача определения среднего значения энергии частицы, гармонически колеблющейся около некоторого центра, была решена в 1900 г., когда М.Планком была получена следующая формула для < W >:
<W>=
При высокой температуре, когда kТ >> hn, показательная функция ex = I + x Тогда формула (7) приводит к классическому результату (I): < W > = Таким образом, при высоких температурах средняя энергия, приходящаяся на одну колебательную степень свободы атома, не зависит от частоты n его колебаний. В этих условиях для теплоёмкости твёрдого тела справедлив закон Дюлонга и Пти (4). При низких температурах положение существенным образом изменяется. Если kT<< hn, или Поэтому в знаменателе формулы (7) можно пренебречь единицей. Тогда средняя энергия < W > оказывается равной
< W > =
то есть очень быстро убывает с уменьшением температуры. Квантовые представления позволяют объяснить, почему теплоёмкость стремится к нулю при Т ® 0: при очень низких температурах расстояние между соседними энергетическими уровнями велико и нагревание твёрдого тела на 1° не может перевести атомы с самого низкого энергетического уровня на следующий уровень, то есть kT значительно меньше, чем высота hn одной "ступеньки" энергетической лестницы (6). Температура Тс, при которой теплоёмкость твёрдого тела начинает быстро уменьшаться, определяется из условия
kTс= h·nмакс , (9)
где nмакс - наибольшая частота колебаний атомов в решётке твёрдого тела. Температуру Тс называют характеристической температурой Дебая. При Т >> Tс cправедлив закон Дюлонга и Пти.
МЕТОД ОПРЕДЕЛЕНИЯ ТЕПЛОЁМКОСТИ ТВЁРДОГО ТЕЛА
В данной работе металлический образец нагревается до определённой температуры и охлаждается в воздухе. Количество теплоты q, теряемой образцом металла за промежуток времени dt, записывается выражением:
где Т - температура образца, С - удельная теплоёмкость металла, Интегрирование проводится по объёму образца V. Это же количество теплоты может быть выражено из закона Ньютона: q = где T0 - температура окружающей среды (воздуха), a - коэффициент теплоотдачи от охлаждаемого образца к воздуху. Интегрирование проводится по поверхности образца (S). Тогда
Так как величины
Отсюда, заменив произведение объёма на плотность образца массой m, получим:
Интегрируя (14), получим: T – T0 = (Tm – T0)
где Tm - температура тела в начальный момент времени (t = 0). Логарифмируя выражение (15), имеем:
Примечание. Следует иметь в виду, что операция логарифмирования именованных (имеющих размерности) величин не имеет смысла, поэтому будем считать, что мы логарифмируем алгебраическое выражение.
Уравнение (16) есть уравнение прямой. Величина Имея графики, соответствующие формуле (16) для двух образцов, отличающихся друг от друга теплоёмкостями и массами (величины a и S принимаем одинаковыми в одних и тех же интервалах температур), определяем по ним отношения к1 и к2 этих двух графиков и выполняем следующие преобразования:
в результате получаем рабочую формулу:
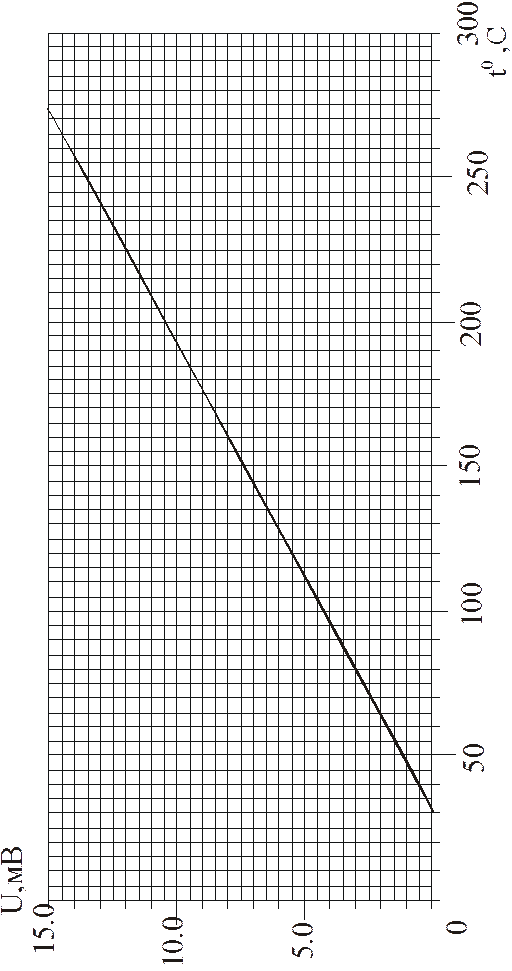
ПРАКТИЧЕСКАЯ ЧАСТЬ Для нагрева образцов (см. рис.2) служит электропечь А. Термопары С укреплены на подвижной планке, а их спаи зачеканены в образцы В, представляющие собой металлические цилиндры длиной 60 мм и диаметром 9 мм. Сигнал с термопар в милливольтах поступает на цифровой вольтметр. Для перевода показаний вольтметра из мВ в °С прилагается градуировочная характеристика (см. рис.1). Температура образца равна сумме температур термопары и окружающей среды t0 (воздуха в лаборатории), определяемой по термометру в помещении, поэтому для определения истинной температуры образца из полученного значения необходимо вычесть величину температуры в помещении. Принадлежности: 1. Электропечь. 2. Набор образцов с термопарами (масса медного образца 34,0 г; масса неизвестного образца 10,3 г). 3. Вольтметр цифровой. 4. Секундомер. 5. График градуировки термопары (рис. 3). 6. График теплоёмкости медного образца (рис.4). 7. Термометр бытовой. Порядок выполнения работы:
3.1. Убедитесь в наличии и целостности заземляющего провода, присоединённого к корпусу электропечи и к заземляющей шине лабораторного помещения. 3.2. Включите сетевые шнуры электропечи и вольтметра в розетки ~ 220 В. 3.3. Подключите к гнёздам вольтметра штекеры термопарных проводов, утопите на вольтметре кнопку «=». В случае появления на шкале знака “-“ поменяйте штекеры в гнёздах местами.
3.4. Определите по красному цвету торца медный образец, поднимите подвижную планку электропечи до отказа вверх, затем подведите образец к горловине печи и опустите его внутрь печи до упора планки. 3.5. Запишите в таблицу по показаниям бытового термометра значение температуры воздуха t0 в помещении. 3.6. Переведите переключатель на панели планки в сторону термопары, помещённой вместе с образцом в печь. 3.7. Нажмите на корпусе печи кнопку подачи напряжения - загорится сигнальная лампа, начнётся нагрев печи. 3.8. Следя за показаниями вольтметра, нагрейте печь с образцом до показания, соответствующего температуре 250°С (для перевода показаний в милливольты воспользуйтесь градуировочным графиком термопары). Обратите внимание на то, что показания на шкале вольтметра отображаются в Вольтах. 3.9. По достижении заданной температуры поднимите планку вверх до выхода образца из горловины печи, одновременно включите секундомер и поверните планку на 90 градусов. Отключите питание электропечи кнопкой на её корпусе. 3.10. В процессе охлаждения образца до 100 0С каждые 30 секунд без остановки секундомера записывайте в таблицу 1 показания вольтметра в милливольтах, то есть значения на шкале вольтметра умножайте на 103, с точностью до десятых. 3.11. Выполните в том же порядке нагрев неизвестного образца (не забудьте переместить переключатель термопар в сторону нагреваемой термопары), по окончании нагрева обесточьте электропечь кнопкой на её корпусе. Данные занесите в таблицу 2. 3.12. Отсоедините от сети ~220 В провод электропитания установки.
Таблица 1(2)
3.13. С помощью градуировочной характеристики переведите полученные значения температур из мВ в °С, рассчитайте разности температур (t - t0) и определите значения натуральных логарифмов этих разностей. 3.14. По данным опыта отдельно для каждого из образцов постройте на миллиметровках формата А4 графики зависимостей ln(t - t0) = f (t), где по осям ординат откладывайте значения функции, а по осям абсцисс - значения аргумента. 3.15. Из построенных графиков определите величины к1 и к2 графиков (см. листы 7,8) и рассчитайте величину b = k1 / k2. 3.16. Вычислите по формуле (17) значение теплоёмкости неизвестного металла С2 с точностью до тысячных для температуры 20 0С, при этом значение С1 для меди возьмите из таблицы 3. 3.17. Полученное значение теплоёмкости неизвестного металла запишите в протокол измерений, по таблице 3 определите неизвестный металл по наиболее близкому значению теплоёмкости в сравнении с полученным значением и внесите его наименование также в протокол. 3.18. Рассчитайте относительную погрешность
Таблица 3
4. КОНТРОЛЬНЫЕ ВОПРОСЫ (ПРИМЕРНЫЕ):
4.1. Что называется теплоёмкостью? В каких единицах она измеряется? 4.2. Почему при точных измерениях величины U и I нельзя измерять стрелочными приборами? 4.3. Что называется удельной (молярной) теплоёмкостью? 4.4. Как зависит теплоёмкость вещества от характера термодинамического процесса? 4.5. Какое свойство вещества характеризует теплоёмкость? 4.6. Сформулируйте закон Дюлонга и Пти. Когда справедлив этот закон? 4.7. Как зависит теплоёмкость тела от его температуры? 4.8. В чём заключается данный метод определения теплоёмкости металла? ЛИТЕРАТУРА
5.1. А.А. Детлаф, Б.М. Яворский, Л.Б. Милковская, Курс физики, т.1. 5.2. И.К. Кикоин, А.К.Кикоин, Молекулярная физика, гл.9.
|






 , где к = 1,380662·10-23
, где к = 1,380662·10-23  (постоянная Больцмана).
(постоянная Больцмана). = 3R = 25
= 3R = 25 
 = 5,97
= 5,97  (4)
(4) Сm
Сm (5)
(5) (n = 0, 1, 2, 3, …..) (6)
(n = 0, 1, 2, 3, …..) (6) , которая сохраняется даже при абсолютном нуле температуры. Эта энергия не связана с тепловым движением атомов и не влияет на теплоёмкость кристаллов.
, которая сохраняется даже при абсолютном нуле температуры. Эта энергия не связана с тепловым движением атомов и не влияет на теплоёмкость кристаллов. (7)
(7) близка к единице и можно воспользоваться следующей приближённой формулой, справедливой при х << I:
близка к единице и можно воспользоваться следующей приближённой формулой, справедливой при х << I:
 >>1, то
>>1, то  .
. , (8)
, (8) , (10)
, (10) - его плотность.
- его плотность. , (11)
, (11) -
-  (12)
(12) , C,
, C,  (13)
(13) (14)
(14) , (15)
, (15) (16)
(16) представляет собой отношение величин катета ординаты к1 = ln (T – T0) к катету абсциссы к2 = t треугольника, гипотенузой которого является прямая графика. Получив из опыта значения температуры образца для ряда значений времени, нужно взять логарифмы от величин (Т – Т0) или, что одно и то же, от величин (t – t0) и на миллиметровке построить график зависимости полученных значений от времени.
представляет собой отношение величин катета ординаты к1 = ln (T – T0) к катету абсциссы к2 = t треугольника, гипотенузой которого является прямая графика. Получив из опыта значения температуры образца для ряда значений времени, нужно взять логарифмы от величин (Т – Т0) или, что одно и то же, от величин (t – t0) и на миллиметровке построить график зависимости полученных значений от времени.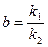 , где
, где  ,
,  ,
,  ,
, (17)
(17)
 (%) полученной величины теплоёмкости установленного металла по сравнению с табличным значением.
(%) полученной величины теплоёмкости установленного металла по сравнению с табличным значением.