 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рассмотрим некоторые из названных и другие величины
Лабораторная работа №3 Изучение законов вращательного движения с помощью маятника Обербека Студент должен знать: Величины, характеризующие кинематику вращательного движения, момент инерции и единицы его измерения. Момент инерции различных тел (с выводом формул для стержня, тонкого кольца, тонкой сферы и др.). Момент силы (векторная форма записи), направление и единицы его измерения. Основное уравнение динамики вращательного движения. Закон сохранения момента количества движения (привести примеры использования его на практике). Сочленения и рычаги в опорно-двигательном аппарате человека. Центрифугирование. Студент должен уметь: Работать с экспериментальной установкой, пользоваться формулами для подсчета измеряемых величин в международной системе единиц СИ, производить оценку погрешностей измерений. Краткая теория Простейшим случаем вращательного движения является вращение твердого тела вокруг неподвижной оси. При этом все точки тела описывают окружности, центры которых лежат на одной прямой, являющейся осью вращения. Вращательное движение удобно характеризовать углом поворота «j», угловой скоростью « Аналогом величин, характеризующих поступательное движение во вращательном движении вокруг неподвижной оси являются: 1) пройденный путь S - угол поворота j; 2) линейная скорость u = dS/dt - угловая скорость 3) ускорение 4) масса тела m - момент инерции J вращающейся материальной точки массой m относительно оси неподвижной оси на расстоянии r: J = mr2 , а для любого тела - 5) сила 6) импульс тела Рассмотрим некоторые из названных и другие величины Угловая скорость При изменении угловой скорости вводят понятие углового ускорения:
Угловое ускорение
Т.к. где Для характеристики динамики вращательного движения вводятся понятия момента силы и момента инерции. Рассмотри движение материальной точки "А" с массой m по окружности радиусом r (рис. 1). Пусть на точку "А" массой m действует сила Ft = F Sina = m Так как F Sina = mre (2) Умножив правую и левую часть равенства (2) на r получим: Fr Sina = mr2e или M =Je , отсюда:
где М=FrSina или в векторной форме: J=mr2 - момент вращения материальной точки А массой m относительно оси «О». Зависимость
Рис.1 Вращение материальной точки А массой m относительно оси «О» Это же выражение справедливо и для характеристики вращательного движения твердого тела с учетом того, что J - момент инерции тела, характеризующий его инерционное свойство во вращательном движении относительно какой-либо оси. Для определения момента инерции твердого тела необходимо разбить тело на бесконечно малые элементы с массой dm, найти моменты инерции каждого элемента dJ и проинтегрировать их. Каждый элемент можно приближенно принять за материальную точку c
Для тел различной геометрической формы момент инерции рассчитывается по формулам; полученным при интегрировании выражения (4), например: 1)для однородного сплошного цилиндра (диска) относительно продольной оси J=mR2/2, где m - масса цилиндра, R - его радиус; 2) для однородного сплошного цилиндра (стержня) относительно поперечной оси, проходящей через его середину
3) для однородного шара радиуса R , массой m относительно оси, проходящей через его середину 4) для тонкого однородного кольца (обруча) радиуса R массой m относительно оси, проходящей через центр перпендикулярно к плоскости кольца J = mR2 и т.д. Основное уравнение динамики вращательного движения тела можно записать в ином виде, учитывая, что
Величина Приведенное равенство (5) показывает, что изменение момента количества движения вращающегося тела равно импульсу момента приложенных к нему сил. Если Это следствие называется законом сохранения момента количества движения: если сумма моментов сил Изучение законов вращательного движения в лабораторной работе производится с помощью маятника Обербека, который представляет собой крестовину, состоящую из 4-х стержней каждый длиной l/2, прикрепленных к втулке с осью (рис.2). На стержнях фиксируются грузы массой m1, которые могут быть закреплены симметрично на различных расстояниях от оси вращения. На шкив радиусом r, находящийся на оси вращения, наматывается нить, к свободному концу которой прикрепляется груз Р. Если предоставить грузу Р возможность двигаться, то это падение будет происходить с ускорением а. При этом шкив со стержнями и расположенными на них грузами будет вращаться с угловым ускорением e, которое можно найти, измерив высоту h и время падения груза t.
где r - радиус шкива, на который наматывается нить. Силой, создающей вращающий момент, является сила натяжения нити Т. Из второго закона Ньютона для груза Р следует T = P - ma = mg - ma = m(g-a) .(7) Тогда вращающий момент M = Tr = m(g-a)r . (8) Момент инерции маятника может быть определен из основного уравнения вращательного движения: J = M/e . (9) Подставляя в формулу (9) формулы (5) и (7) получим окончательное выражение для момента инерции маятника Обербека, определенного практически (экспериментально:
С другой стороны, теоретически, момент инерции маятника может быть найден из формулы Jтеорет Тогда момент инерции крестовины теоретически определяется по формуле:
где m2 - масса «двойного» стержня, l – его длина (см. рис.2).
Выполнение работы 1. Грузы m1 на маятнике Обербека (крестовине) закреплены на некотором одинаковом расстоянии R от оси вращения (рис.2). 2. Измерить расстояние R от оси вращения до центра масс груза m1. 3. Намотать нить на шкив крестовины и последнюю придерживать рукой. 4. Подвесить к нити груз массой m (100, 200 или 300 гр) и совместить нижнюю часть груза с верхней меткой на стене. 5. Дать возможность грузу массой m опускаться. Измерить время движения t груза на расстоянии h = 0,5 м от верхней до нижней меток на стене. 6. Результаты измерений занести в таблицу 1. Измерения провести при двух различных грузах массой m по 3 раза с каждым при h=const. По формулам 11, 12, 13 (см. ниже) по средним значениям «t» вычислить линейное ускорение « a», угловое ускорение «e», вращающий момент « M», действующий на маятник и по формуле «14» момент инерции, найденный практически – - « Jпракт ».
где r – радиус шкива, на который наматывается нить.
Jпракт = М / e (14) Вычислить теоретически момент инерции «Jтеорет» по формуле (15) и сравнить с результатом в пункте 8 (формула 14).
Сравнивая Jпракт = М / e , найденный из основного уравнения динамики вращательного движения (e= M/J), с его теоретическим значением 1. Вычислить абсолютную по формуле (16) и относительную по формуле (17) погрешность измерений для одной из серий результатов. Таблица 1
Вычисление погрешностей 1. Абсолютная погрешность измерения практического значения момента инерции маятника Обербека: где 2. Относительная погрешность измерения практического значения момента инерции маятника Обербека:
Рис.2 Маятник Обербека m1=154 г =0,154 кг– масса каждого груза на стержне, m2 =184 г=0,184 кг – масса каждого из 2-х стержней, l =52 cм=0,52 м – длина стержня, r =1 см=0,01 – радиус шкива, g =9,8 м/с2, h =0,5 м, Dh =1см. |



 », т.к. все токи при таком вращении поворачиваются на один и тот же угол «j», движутся с одинаковой угловой скоростью «
», т.к. все токи при таком вращении поворачиваются на один и тот же угол «j», движутся с одинаковой угловой скоростью «  = dj/dt;
= dj/dt; -угловое ускорение
-угловое ускорение  ;
; ;
;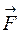 - момент силы
- момент силы  , характеризующий вращающее действие силы;
, характеризующий вращающее действие силы; - момент импульса тела
- момент импульса тела  .
. [e] = 1 рад/с2 (1/с2).
[e] = 1 рад/с2 (1/с2). - вектор, совпадающий по направлению с угловой скоростью при ускоренном движении и противоположной ей – при замедленном. Угловое ускорение связано с тангенциальным (касательным) ускорением
- вектор, совпадающий по направлению с угловой скоростью при ускоренном движении и противоположной ей – при замедленном. Угловое ускорение связано с тангенциальным (касательным) ускорением  :
:
 , то
, то 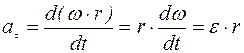 ,
, - линейная скорость
- линейная скорость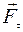 :
: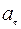 (1)
(1) /J, (3)
/J, (3) = [
= [  ] - вращающий момент (момент силы
] - вращающий момент (момент силы  =
= 
 , тогда:
, тогда: или
или  (4)
(4) , где m – масса стержня, l – его длина.
, где m – масса стержня, l – его длина.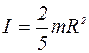
 ,
,  или
или (5)
(5) dt называется импульсом момента сил, приложенных к телу, а d(
dt называется импульсом момента сил, приложенных к телу, а d(  ) - изменение момента количества движения тела (момента импульса тела).
) - изменение момента количества движения тела (момента импульса тела). )= 0 или J
)= 0 или J  = const , т.е. момент количества движения остается постоянным.
= const , т.е. момент количества движения остается постоянным. , действующих на тело, равна нулю (
, действующих на тело, равна нулю (  остается постоянным (
остается постоянным ( 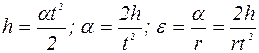 (6)
(6) +
+  =m
=m  . Переходя от векторной суммы к алгебраической, проектируя на ось ОХ имеем: Р - Т = ma, откуда
. Переходя от векторной суммы к алгебраической, проектируя на ось ОХ имеем: Р - Т = ma, откуда . (10)
. (10) Jk + 4Jrp (моментом инерции цилиндра радиуса r пренебрегаем), где Jk - момент инерции крестовины, Jrр - момент инерции груза относительно оси вращения. Считая груз материальной точкой массой m1, его момент инерции можно найти по формуле Jrp= m1R2, где R - расстояние от оси вращения до центра масс груза.
Jk + 4Jrp (моментом инерции цилиндра радиуса r пренебрегаем), где Jk - момент инерции крестовины, Jrр - момент инерции груза относительно оси вращения. Считая груз материальной точкой массой m1, его момент инерции можно найти по формуле Jrp= m1R2, где R - расстояние от оси вращения до центра масс груза.

 (11)
(11) (12)
(12) (13)
(13) (15)
(15) в работе проверяется справедливость основного уравнения динамики вращательного движения e = M/J.
в работе проверяется справедливость основного уравнения динамики вращательного движения e = M/J. м/с2
м/с2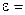 a/r 1/с2
a/r 1/с2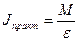 кг.м2
кг.м2 кг.м2
кг.м2 , (16)
, (16) .
. (17)
(17)