 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Визуализация метода Ньютона
Методические указания по выполнению лабораторных работ по дисциплине Б.2.2.3«Вычислительная математика»
Направления подготовки ( 09.03.01 ) 230100.62 "Информатика и вычислительная техника"
Лабораторная работа № 2
Применения метода Ньютона для нелинейных уравнений. Программная реализация.
Аннотация цель данной лабораторной работы является сформирование навыков численного решения нелинейных уравнений и систем нелинейных уравнений.
Теоретические указания к работе. Классический метод Ньютона или касательных заключается в том, что если Уравнение касательной к функции
В уравнении касательной положим Тогда алгоритм последовательных вычислений в методе Ньютона состоит в следующем:
Сходимость метода касательных квадратичная, порядок сходимости равен 2. Таким образом, сходимость метода касательных Ньютона очень быстрая. Запомните этот замечательный факт! Без всяких изменений метод обобщается на комплексный случай. Если корень Упражнение 1. Найти с помощью метода касательных решение уравнения Упражнение 2. Найти с помощью метода касательных решение уравнения К недостаткам метода Ньютона следует отнести его локальность, поскольку он гарантированно сходится при произвольном стартовом приближении только, если везде выполнено условие Недостатком метода Ньютона является необходимость вычисления производных на каждом шаге. Визуализация метода Ньютона Метод Ньютона (метод касательных) применяется в том случае, если уравнение f(x) = 0 имеет корень 1) функция y= f(x) определена и непрерывна при 2) f(a)·f(b) < 0 (функция принимает значения разных знаков на концах отрезка [a;b]); 3) производные f'(x) и f''(x) сохраняют знак на отрезке [a;b] (т.е. функция f(x) либо возрастает, либо убывает на отрезке [a;b], сохраняя при этом направление выпуклости); 4) Основная идея метода заключается в следующем: на отрезке [a;b] выбирается такое число x0, при котором f(x0) имеет тот же знак, что и f''(x0), т. е. выполняется условие f(x0)·f''(x) > 0. Таким образом, выбирается точка с абсциссой x0, в которой касательная к кривой y=f(x) на отрезке [a;b] пересекает ось Ox. За точку x0 сначала удобно выбирать один из концов отрезка. Рассмотрим метод Ньютона на конкретном примере. Пусть нам дана возрастающая функция y = f(x) =x2-2, непрерывная на отрезке (0;2), и имеющая f '(x) = 2x > 0 и f ''(x) = 2 > 0.
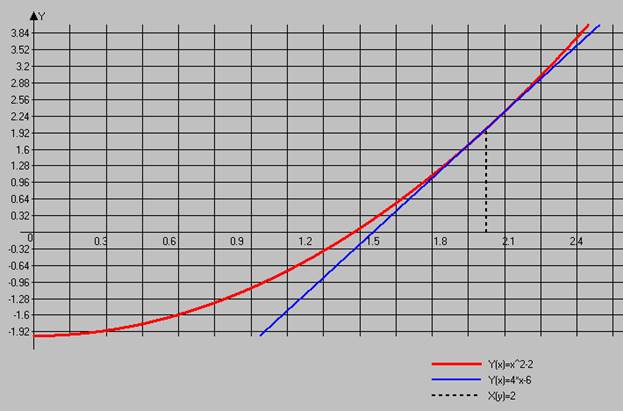
Рисунок 1. f(x) =x2-2 Уравнение касательной в общем виде имеет представление: y-y0= f '(x0)·(x-x0). В нашем случае: y-y0=2x0·(x-x0). В качестве точки x0 выбираем точку B1(b; f(b)) = (2,2). Проводим касательную к функции y = f(x) в точке B1, и обозначаем точку пересечения касательной и оси Ox точкой x1. Получаем уравнение первой касательной:y-2=2·2(x-2), y=4x-6. Точка пересечения касательной и оси Ox: x1 =
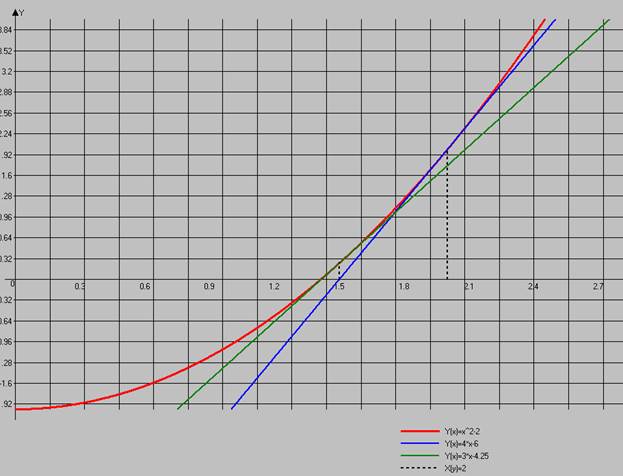
Рисунок 2. Результат первой итерации Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x1, получаем точку В2 =(1.5; 0.25). Снова проводим касательную к функции y = f(x) в точке В2, и обозначаем точку пересечения касательной и оси Ox точкой x2. Уравнение второй касательной: y-2.25=2*1.5(x-1.5), y = 3x – 4.25. Точка пересечения касательной и оси Ox: x2=
Рисунок3.Вторая итерация метода Ньютона Затем находим точку пересечения функции y=f(x) и перпендикуляра, проведенного к оси Ox через точку x2, получаем точку В3 и так далее. В3 = (
Рисунок4.Третий шаг метода касательных Первое приближение корня определяется по формуле:
Второе приближение корня определяется по формуле:
Третье приближение корня определяется по формуле:
Таким образом,i-ое приближение корня определяется по формуле:
Вычисления ведутся до тех пор, пока не будет достигнуто совпадение десятичных знаков, которые необходимы в ответе, или заданной точности e - до выполнения неравенства |xi-xi-1| <e.
Задание к Лабораторной Работе.
1.Решить трансцендентное и алгебраическое уравнение, методом Ньютона. 2. Описать в отчёте численную методику решения 3. Привести отчёт
Техническое обеспечение для выполнения лабораторной работы.
Для проведения лабораторных занятий требуется компьютерный класс, оборудованный ПЭВМ в конфигурации не худшей чем: процессор Pentium IV 3 ГГц, ОЗУ 2 Гбайта, НЖМД 200 Гбайт c установленными операционными системами семейств Microsoft Windows 7, c установленной IDE Microft Visual Studio Express.
Требования к отчету. Отчет по лабораторной работе должен соответствовать следующей структуре. 1. Титульный лист. 2. Словесная постановка задачи. В этом подразделе проводится полное описание задачи. Описывается суть задачи, анализ входящих в нее физических величин, область их допустимых значений, единицы их измерения, возможные ограничения, анализ условий при которых задача имеет решение (не имеет решения), анализ ожидаемых результатов. 3. Математическая модель. В этом подразделе вводятся математические описания физических величин и математическое описание их взаимодействий. Цель подраздела – представить решаемую задачу в математической формулировке. 4. Алгоритм решения задачи. В подразделе описывается разработка структуры алгоритма, обосновывается абстракция данных, задача разбивается на подзадачи. Схема алгоритма выполняется по ЕСПД (ГОСТ 19.003-80 и ГОСТ 19.002-80). 5. Листинг программы. Подраздел должен содержать текстпрограммы реализованной в среде Microsoft Visual Studio Express. 6. Контрольный тест. Подраздел содержит наборы исходных данных и полученные в ходе выполнения программы результаты. (Приведены в приложении 1) 7. Выводы по лабораторной работе.
|



 — некоторое приближение к корню
— некоторое приближение к корню  уравнения
уравнения  , то следующее приближение определяется как корень касательной к функции
, то следующее приближение определяется как корень касательной к функции  , проведенной в точке
, проведенной в точке  в точке
в точке  имеет вид:
имеет вид:
 и
и  .
.
 на отрезке (0, 2).
на отрезке (0, 2). на отрезке (1, 3).
на отрезке (1, 3). , в противной ситуации сходимость есть лишь в некоторой окрестности корня.
, в противной ситуации сходимость есть лишь в некоторой окрестности корня.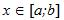 , и выполняются условия:
, и выполняются условия: ;
; .
.

 .
.
 )
)
 = 1.5.
= 1.5.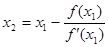 =
= 


