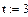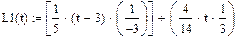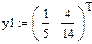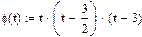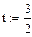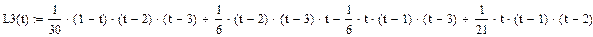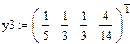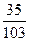 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Интерполяционный многочлен Лагранжа
Лабораторная работа №1 Интерполирование функций в MathCAD Цель работы:изучить некоторые возможности аппроксимации опытных данных, которые предоставляются программной средой MathCAD; получить представление об интерполировании функций как классическом методе аппроксимации; осуществить сравнительный анализ различных способов интерполяции и научиться оценивать погрешность многочленной интерполяции. Интерполяция Для построения интерполяции-экстраполяции в MathCAD имеются несколько встроенных функций, позволяющих "соединить" точки выборки данных Примечание. Будем использовать вместо обозначения Линейная интерполяция Самый простой вид интерполяции - линейная, которая представляет искомую зависимость Для построения линейной интерполяции служит встроенная функция linterp. - linterp (
Элементы вектора Пример 1. Линейная интерполяция (рис. 1)
Рис. 1. Линейная интерполяция (пример 1) Как видно из примера 1, чтобы осуществить линейную интерполяцию, надо выполнить следующие действия: 1) Введите векторы данных 2) Определите функцию linterp ( 3) Вычислите значения этой функции в требуемых точках, например linterp( Примечание. Обратите внимание, что функция Сплайн-интерполяция Сплайн — это функция, которая на каждом частичном отрезке интерполяции является алгебраическим многочленом, а на всем заданном отрезке непрерывна вместе с несколькими своими производными. В большинстве практических приложений желательно соединить экспериментальные точки не ломаной линией, а гладкой кривой. Лучше всего для этих целей подходит интерполяция кубическими сплайнами, т. е. отрезками кубических парабол. Смысл кубической сплайн-интерполяции заключается в том, что в промежутках между точками осуществляется аппроксимация в виде зависимости - interp(s, s - вектор вторых производных, созданный одной из сопутствующих функций cspline, pspline или lspline;
порядке возрастания;
Пример 2. Кубическая сплайн-интерполяция (рис.2)
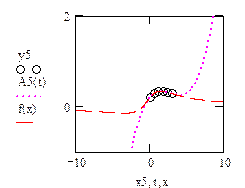
Рис.2. Кубическая сплайн-интерполяция (пример 2)
Рис.3. Примеры сплайн-интерполяций Сплайн-интерполяция в MathCAD реализована чуть сложнее линейной. Перед применением функции interp необходимо предварительно определить первый из ее аргументов - векторную переменную s. Делается это при помощи одной из трех встроенных функций тех же аргументов - lspline( - pspline( - cspline( - Интерполяционный многочлен Лагранжа Пусть известные значения некоторой функции
При этом требуется получить значение функции Очевидный прием решения этой задачи — вычислить значение f(x), воспользовавшись аналитическим выражением функции f. Этот прием, однако, можно применить лишь в случае, когда аналитическое выражение f пригодно для вычислений. Более того, часто аналитическое выражение функции
Классический подход к решению задачи построения приближающей функции основывается на требовании строгого совпадения значений f(x) и F(x) в точках
В этом случае нахождение приближенной функции называют интерполяцией (или интерполированием), а точки Интерполяционным многочленом Лагранжа называется многочлен, представленный в виде
где Интерполяционным многочленом Лагранжа можно записать иначе:
По таблице исходной функции Пример 3.Построить интерполяционный многочлен Лагранжа для функции, заданной таблицей:
Решение: Из таблицы следует, что
По формуле получим:
Формула Лагранжа для равноотстоящих узлов принимает вид:
где Пример 4. Составить интерполяционный многочлен Лагранжа для функции, заданной своими значениями наравноотстоящих узлах (п = 2, h = 1):
Решение: Используя формулу запишем:
Узловые табличные значения функции (4; —2; 6) получаются по этой формуле соответственно при t = 0; 1; 2. Оценка погрешности формулы Лагранжа находится по формуле:
где Пример 5.Для заданной функции 1. Построить интерполяционный многочлен Лагранжа 2. Используя MathCAD, выполнить интерполяцию кубическим сплайном. Оценить погрешность. Решение: 1.
Для составления полинома Лагранжа можно воспользоваться средствами MathCAD.
Чтобы упростить выражение, полученное по формуле, необходимо воспользоваться оператором упрощения в MathCAD. Упрощение выражений - наиболее часто применяемая операция. Символьный процессор MathCAD стремится так преобразовать выражение, чтобы оно приобрело более простую форму. При этом используются различные арифметические формулы, приведение подобных слагаемых, тригонометрические тождества, пересчет обратных функций и др. Чтобы упростить выражение с помощью меню: 1) Введите выражение. 2) Выделите выражение целиком или его часть, которую нужно упростить. 3) Выберите команду Symbolics / Simplify (Символика / Упростить).
В среде MathCAD получили:
В среде MathCAD получили:
2)
3)
|
кривой разной степени гладкости. По определению, интерполяция означает построение функции 
, аппроксимирующей зависимость 
в промежуточных точках отрезка 
. Поэтому интерполяция есть один из методов аппроксимации. В точках 
значения интерполяционной функции должны совпадать с исходными данными, т. е. 
.
, чтобы не путать вектор данных 
и скалярную переменную 
.
, 
.
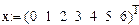
. Коэффициенты a, b, c, d рассчитываются независимо для каждого промежутка, исходя из значений 
в соседних точках. Этот процесс скрыт от пользователя, поскольку смысл задачи интерполяции состоит в выдаче значения 
.
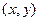образуют следующую таблицу: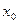
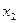
, но не совпадает ни с одним из значений 
.
.
, 
, …, 
.
- узлами интерполяции.
,
- вспомогательный многочлен.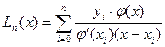
.
формула позволяет весьма просто составить «внешний вид» многочлена.
(т.е. степень многочлена будет не выше, чем вторая);
,
,
+ 
+ 
,
, 
, 
;
.
,
, 
, 
, 
.
,
.
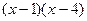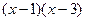на отрезке 
:
при 
для равноотстающих узлов. Построить графики получившихся полиномов.
, 
использовать 
и 
соответственно. Оценить погрешность (построить графики погрешности). Оценить зависимость погрешности интерполяции от порядка многочлена.
