 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Точка над буквой означает, что эва величина является вектором изображённым на комплексной плоскости. Т.е это вектор выраженный в комплексной форме. 12
Лекция №13 Рабочий процесс трансформатора Основные формулы и уравнения трансформатора
К первичной обмотке трансформатора подводится синусоидальное напряжение
u1 = Um sin ωt, (13.1)
благодаря чему по этой обмотке проходит переменный ток
i1=Im sin ωt, (13.2)
создающий переменный магнитный поток
ф=Фm sin ωt (13.3)
где Фmax — максимальное значение потока,
практически совпадающий по фазе с током I1. Переменный поток наводит в обмотках трансформатора ЭДС
е1= - w1 е2= - w2
Рассмотрев формулы (13.1-13.5) и произведя ряд преобразований получим формылы действующего значения ЭДС обмоток трансформатора
где
Е1 и Е2 действующее значение ЭДС первичной и вторичной обмоток; f - частота сети, Гц (герц); w1 и w2 - число витков, соответственно, первичной и вторичной обмоток; Фm - максимальное значение результирующего магнитного потока.
Примечание: вывод формул см литературу "Кацман М.М. Электрические машины." §1.4
Из формул 13.6 и 13.7 можно получить выражение коэффициента трансформации Отношение ЭДС обмотки высшего напряжения к ЭДС обмотки низшего напряжения называют коэффициентом трансформации:
При практических расчетах коэффициент трансформации с некоторым допущением принимают равным отношению номинальных напряжений обмоток ВН и НН:
Рис. 13.1 Магнитные потоки в однофазном трансформаторе
Токи I1 и I2 в обмотках трансформатора помимо основного магнитного потока Ф создают магнитные потоки рассеяния
где
Так как магнитные потоки рассеяния замыкаются главным образом в немагнитной среде (воздух, масло, медь), магнитная проницаемость которой постоянна, то и индуктивности Ls1 и Ls2 можно считать постоянными. Действующие значения ЭДС рассеяния пропорциональны токам в соответствующих обмотках:
где x1 и x2 — индуктивные сопротивления рассеяния первичной и вторичной обмоток соответственно, Ом (знак минус в этих выражениях свидетельствует о реактивности ЭДС рассеяния). Таким образом, в каждой из обмоток трансформатора индуцируются по две ЭДС: - ЭДС от основного потока Ф и - ЭДС от потока рассеяния ( Для первичной цепи трансформатора, включенной в сеть на напряжение
или, перенеся ЭДС
Точка над буквой означает, что эва величина является вектором изображённым на комплексной плоскости. Т.е это вектор выраженный в комплексной форме. j = ЭДС первичной обмотки Обычно индуктивное
Для вторичной цепи трансформатора, замкнутой на нагрузку с сопротивлением
Из этого уравнения следует, что напряжение на выходе нагруженного трансформатора отличается от ЭДС вторичной обмотки на величину падения напряжений в этой обмотке.
Путём аналогичных рассуждений, можно получить уравнение МД
и уравнение токов трансформатора
где Другими словами, это такой ток, который в обмотке с числом витков w1 создает такую же МДС, что и ток I2 во вторичной обмотке w2, т. е. Преобразовав выражение (13.17), получим уравнение токов трансформатора:
12 |



 (13.4)
(13.4) (13.8)
(13.8) (13.9)
(13.9)
 и
и  (рис. 13.1), каждый из которых сцеплен с витками лишь собственной обмотки и индуцирует в ней ЭДС рассеяния. Эти ЭДС в первичной и вторичной обмотках таковы:
(рис. 13.1), каждый из которых сцеплен с витками лишь собственной обмотки и индуцирует в ней ЭДС рассеяния. Эти ЭДС в первичной и вторичной обмотках таковы: (13.10)
(13.10) и
и  — индуктивности рассеяния.
— индуктивности рассеяния. (13.11)
(13.11) , с учетом падения напряжения в активном сопротивлении первичной обмотки
, с учетом падения напряжения в активном сопротивлении первичной обмотки  можно записать уравнение напряжений по второму закону Кирхгофа:
можно записать уравнение напряжений по второму закону Кирхгофа: (13.12)
(13.12) и
и  в правую часть уравнения и выразив ЭДС рассеяния через индуктивное сопротивление рассеяния
в правую часть уравнения и выразив ЭДС рассеяния через индуктивное сопротивление рассеяния  , получим уравнение напряжений для первичной цепи трансформатора:
, получим уравнение напряжений для первичной цепи трансформатора: (13.14)
(13.14)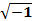 мнимое число
мнимое число , наведенная основным магнитным потоком Ф, представляет собой ЭДС самоиндукции, а поэтому находится в противофазе с подведенным к первичной обмотке напряжением
, наведенная основным магнитным потоком Ф, представляет собой ЭДС самоиндукции, а поэтому находится в противофазе с подведенным к первичной обмотке напряжением  и активное
и активное  падения напряжения невелики, а поэтому с некоторым приближением можно считать, что подведенное к трансформатору напряжение
падения напряжения невелики, а поэтому с некоторым приближением можно считать, что подведенное к трансформатору напряжение 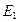 , т. е.
, т. е. (1.14)
(1.14) , уравнение напряжений имеет вид
, уравнение напряжений имеет вид (13.15)
(13.15) (13.16)
(13.16) (13.17)
(13.17) , — ток нагрузки (вторичный ток), приведенный к числу витков первичной обмотки.
, — ток нагрузки (вторичный ток), приведенный к числу витков первичной обмотки.
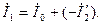 (13.18)
(13.18)