 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ЗАРЯДКЕ И РАЗРЯДКЕ КОНДЕНСАТОРА В
ФГБОУ ВПО «КАЛИНИНГРАДСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ» КАФЕДРА ФИЗИКИ ЛАБОРАТОРНАЯ РАБОТА №104 ИЗУЧЕНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ЗАРЯДКЕ И РАЗРЯДКЕ КОНДЕНСАТОРА В ЭЛЕКТРИЧЕСКОМ «R – C» КОНТУРЕ Методическое указание к выполнению лабораторной работы по разделу «Электричество и магнетизм» для студентов всех форм обучения по всем специальностям
Калининград ОГЛАВЛЕНИЕ Лист 1. ВВЕДЕНИЕ 3 2. ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ЗАРЯДКЕ И РАЗРЯДКЕ КОНДЕНСАТОРА В “R - C” КОНТУРЕ 5 2.1. Расчёт общего вида зависимости напряжения на конденсаторе от времени 5 2.2. Зарядка конденсатора 9 2.3. Разрядка конденсатора 10 2.4. Заключение 10 3. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ 11 Задание №I. Экспериментальное исследование зарядки и разрядки конденсатора большой ёмкости 11 3.1. Экспериментальная часть 11 3.2. Измерения 11 3.3. Обработка результатов 14 Задание №2. Изучение импульсных переходных процессов 17 3.4. Экспериментальная часть 17 3.5. Измерения 18 3.6. Обработка результатов 19 4.ВОПРОСЫ ДЛЯ ПРОВЕРКИ 20 5.ЛИТЕРАТУРА 20 ПРИЛОЖЕНИЕ. Общая характеристика импульсов и способов их формирования в электрических цепях 21
ЦЕЛЬ РАБОТЫ: 1. Ознакомление с классическим методом расчёта переходных процессов при зарядке и разрядке конденсатора. 2. Получение графических зависимостей для напряжения на конденсаторе большой ёмкости в процессе его зарядки и разрядки. 3. Измерение ёмкости конденсатора и сопротивления резистора. 4. Изучение импульсных режимов для переходных процессов в “R – C” контуре с помощью осциллографа.
ИСПОЛЬЗУЕМЫЙ РЕКВИЗИТ: ручной секундомер.
ВВЕДЕНИЕ Электрической цепью называется соединённая металлическими проводами совокупность электрических элементов: источников тока (электрической энергии), преобразователей (например, трансформаторы, выпрямители и т.п.), нагрузок (например, электромоторы, нагреватели, осветители и т.п.), специальных устройств (например, радиопередающие и приёмные установки и т.п.). В электрическую цепь обычно включают также измерительные приборы: амперметры, вольтметры, ваттметры, осциллографы и т.д. В источниках тока в результате работы сторонних сил возникает разность потенциалов на выходных зажимах (клеммах), к которым подключают электрическую цепь. Когда цепь замкнута, в ней протекает электрический ток -постоянный или переменный, в зависимости от типа источника. Все остальные элементы электрической цепи можно обозначить в качестве приёмников (или потребителей) электрической энергии. Вид потребления зависит от назначения приёмников и, соответственно, от их электрических параметров: сопротивления R ёмкости С и индуктивности L . Примечание. Электропараметрами R, C и L , строго говоря, обладают все участки цепи, включая и провода. Однако проявление того или иного параметра зависит от соотношения их численных значений в разных элементах цепи, а также от вида протекающего тока. Электрические цепи, в которых при данном виде тока сопротивлением, ёмкостью и индуктивностью проводов можно пренебречь, а остальные элементы можно по отдельности (условно) рассматривать как резисторы, конденсаторы либо катушки индуктивностей, называются цепями с сосредоточенными параметрами. Электрические цепи, в которых указанные условия не выполняются, называются цепями с распределёнными параметрами. Электрические цепи называются линейными, если значения параметров R , C и L у элементов цепи не зависят от величины протекающего тока. Если параметры R, C и L у элементов цепи зависят от величины протекающего тока, такие цепи называются нелинейными. Электрические цепи с сосредоточенными параметрами графически изображают на схеме с условным обозначением её элементов в виде резисторов, конденсаторов и катушек индуктивностей. Преобразователи типа трансформаторов или выпрямителей имеют свои обозначения. Условные обозначения на схемах имеют коммутирующие устройства (ключи, тумблеры и пр.), измерительные приборы и ряд других элементов. Схемы электрических цепей имеют ветви и узлы.Ветвью называется участок цепи, в котором ток в любой данный момент времени имеет одинаковую величину. Узлом цепи называется место (точка) соединения ветвей. Электрическим контуром называется замкнутый участок цепи, который может состоять из одной ветви или из нескольких ветвей. В последнем случае на разных ветвях контура могут протекать разные токи. В электро- и радиотехнике контуры подразделяются на активные и пассивные. Активным называют контур, содержащий источник тока. Электрические контуры являются основными частями цепей любого назначения: промышленных, бытовых, измерительных, передающих и принимающих радиоустройств, схем ЭВМ и т.д. Например, в радиоустройствах контуры типа R – С - L линейного и нелинейного типа используются для получения гармонических колебаний, радио- и видео- импульсов, в качестве резонаторов для приёма электромагнитных волн и т.д. В схемах ЭВМ R-C контуры широко применяются в качестве дифференцирующих ячеек. Расчёт электрических процессов в любой цепи требует умения вычислять зависимости от времени токов в ветвях и напряжения на элементах, входящих в состав различных контуров. Электрические процессы в цепях подразделяются на два основных типа: установившиеся (на постоянном или переменном токе) и переходные. Теоретическое исследование таких процессов в линейных и нелинейных цепях с распределёнными и сосредоточенными параметрами излагается в специальных курсах (см., например, Зевеке Г.В., Ионкин П.А. и др. "Основы теории цепей",М., Энергия.-1975; Л.Р. Нейман, К.С. Демирчян. "Теоретические основы электротехники",т.1,2, Энергоиздат . - 1981). Для расчётов, в зависимости от вида цепей и протекающих токов, разработано несколько способов: классический, операторный, спектральный, метод дискретных преобразований и ряд других. В данной работе ставится задача ознакомления с переходными процессами в линейном электрическом R - С контуре с сосредоточенными параметрами. Переходным называется процесс перехода от одного установившегося режима к другому. Экспериментальная часть работы состоит из двух заданий. В задании № I изучается процесс перехода конденсатора от незаряженного состояния к заряженному (зарядка конденсатора от выпрямителя с постоянным напряжением); затем - в процессе разрядки - конденсатор возвращается в начальное состояние, т.е. разряжается. Параметры R - С контура в задании № I выбраны таким образом, что процессы зарядки и разрядки происходят достаточно медленно (~ 10 мин). Этим полностью исключается влияние индуктивности цепи и обеспечивается высокая точность измерения зависимости от времени напряжения на конденсаторе с помощью вольтметра, подключённого к пластинам конденсатора. Теоретический расчёт процесса, выполненный классическим методом, приводится в следующем разделе. Задание № 2 состоит в визуальном наблюдении (на экране осциллографа) графиков переходных процессов в R - C контуре при условии, что зарядка конденсатора осуществляется кратковременным импульсом напряжения прямоугольной формы. Здесь электронный луч "рисует" на экране графические зависимости от времени напряжения на элементах контура при зарядке конденсатора (с момента подачи импульса на вход контура) и затем - при разрядке (с момента окончания поданного на вход импульса). Параметры R - C контура в задании № 2 можно изменять с помощью специальных наборов (магазинов) резисторов и конденсаторов. При этом длительность переходных процессов варьируется в пределах (10-3 ÷ 10-6) сек. На экране осциллографа можно наблюдать, что для разных параметров R и С входной (прямоугольный) импульс преобразуется на выходе в импульсы другой формы. Для расчётов таких переходных процессов, когда при действии импульсного напряжения в контуре формируются новые импульсы, при -меняются более сложные, чем классический, способы теоретического исследования. Установлено, что в зависимости от параметров R и С выходное напряжение может быть пропорционально производной по времени либо интегралу от напряжения на входе. Соответственно, такие контуры получили название дифференцирующих и интегрирующих цепочек (ячеек), имеющих широкое применение в разнообразных схемах электроники, в том числе и в схемах ЭВМ. В задании № 2 предусмотрено наблюдение импульсов, формирующихся при переходных процессах в R - С контуре, соответствующих режимам дифференцирования и интегрирования.
ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ ПЕРЕХОДНЫХ ПРОЦЕССОВ ПРИ ЗАРЯДКЕ И РАЗРЯДКЕ КОНДЕНСАТОРА В «R – С» КОНТУРЕ
2.1. Расчёт общего вида зависимости от времени для напряжения на конденсаторе
Данный расчёт выполняется для задания № 1, где предусмотрено достаточно медленное изменение токов и напряжений в контуре. Для этих условий применяются два правила Кирхгофа: а) сумма токов в узлах контура равна нулю; б) сумма падений напряжений в ветвях контура равна сумме ЭДС, Эти правила позволяют получать дифференциальные уравнения, содержащие производные по времени от электрического заряда на конденсаторе. При этом первая производная определяет величину тока, протекающего в ветви с конденсатором. В более общем случае правила Кирхгофа применяют также для расчёта контуров с индуктивностью, где появляется ЭДС индукции, пропорциональная производной по времени от величины тока, т.е. второй производной от электрического заряда. Следовательно, на основе правил Кирхгофа могут получаться дифференциальные уравнения как первого, так и второго порядка. Решение таких уравнений представляет содержание классического метода исследования переходных процессов в электрических контурах. Примечание. Решение дифференциальных уравнений состоит, как известно, в их интегрировании. Классический метод позволяет полностью выполнить эту задачу при условии, что напряжение на входе контура постоянно либо изменяется по достаточно простому закону. Кроме того, параметры контура должны быть сосредоточенными и линейными. В некоторых случаях возможна нелинейность параметра, определяемая также достаточно простой зависимостью. Рассмотрим схему (рис.1) электрической цепи, аналогичную той, которая применяется в задании № I.
Электрическая цепь состоит из двух контуров: O-В-Д-О1 и В-М-М1-Д. Схема предусматривает возможность зарядки конденсатора с ёмкостью С через резистор с сопротивлением R1 при замкнутом ключе К от источника с известным напряжением Uвх, а также - разрядки конденсатора через резистор с сопротивлением R2 при Uвх=0 после размыкания ключа К. На схеме изображён регистрирующий прибор - вольтметр, внутреннее сопротивление которого равно r вн и учтено величиной R2 . Для получения общего вида зависимости от времени
Здесь первый контур О-В-Д-О1 содержит источник, резистор R1 и конденсатор C. Второй контур содержит резистор R2 и конденсатор С. Из уравнений (1) поучаем выражение для тока в ветви В-Д:
Запишем формулу (2) в виде:
где
Учтём, что
Уравнение (4) - это дифференциальное уравнение первого порядка с Решением этого уравнения является функция Для нахождения решения применим стандартный, известный из курса математики способ вариации произвольной постоянной. Вначале ищем решение q1 для соответствующего однородного уравнения. Запишем уравнение для q1:
Это уравнение легко решается методом разделения переменных. Разделяя в (5) переменные, получим:
Выполняем в (6) неопредёленное интегрирование:
где Преобразуем (7) к виду:
Для Решение однородного уравнения получаем в виде:
Общее решение Принимая
Выражение (10) и производную по времени, равную:
подставим в уравнение (4) и получим:
Разделяя в (13) переменные и вычисляя определённый интеграл
Здесь при вычислении интеграла принято условие Теперь подставим результат (14) в (10) и запишем:
Окончательное решение неоднородного уравнения находим, учитывая, что
Разделив в (16) на величину ёмкости С и учитывая, что
Рассмотрим два варианта применения (17) для описания переходных процессов при разрядке и зарядке конденсатора.
2.2. Зарядка конденсатора
Пусть начальное напряжение на конденсаторе
Здесь: Если Обозначая в этом случае запишем формулу (18) в виде:
На практике, однако, следует пользоваться формулой типа (18), т.к. напряжение на конденсаторе измеряется постоянно подключённым в контур вольтметром с конечным внутренним сопротивлением
Для измерений при включённом вольтметре с конечным внутренним сопротивлением
где При известной из опыта зависимости
2.3. Разрядка конденсатора
Пусть
В формуле (21) надо учесть, что после размыкания ключа К в схеме рис.1 имеем: Обозначая R2 = Rразр (сопротивление разрядки), запишем (21) в виде:
Сопротивление Rразр на практике может определяться либо величиной внутреннего сопротивления вольтметра, либо суммарным сопротивлением вольтметра и добавочного резистора, подключаемого параллельно вольтметру. Обозначая сопротивление добавочного резистора R02, запишем
Из (22) получаем: R2 = Rразр = Формулы (21), (22) можно использовать для определения величин Rразр или С, если из опыта известна зависимость от времени для напряжения на конденсаторе при его разрядке. 2.4. Заключение
Отметим, что произведение величин R и С имеет размерность времени - сек. В теории переходных процессов это произведение обозначается Обозначая
Из (23) получаем: Далее, обозначая
Согласно полученному выражению (24) напряжение на конденсаторе при его разрядке в момент времени Отметим также основные результаты проведённого исследования:
1. Формулы (18) - (21а) описывают зависимости от времени напряжения на конденсаторе: - в процессе зарядки при постоянном входном напряжении и начальном напряжении на конденсаторе - в процессе разрядки при некотором начальном напряжении на конденсаторе 2. Условия зарядки и разрядки конденсатора учитывают возможность разных комбинаций включения резисторов, через которые протекают токи за время переходных процессов. 3. При известных (из опыта) зависимостях
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
Примечание. Экспериментальная часть работы содержит два задания. Количество выполняемых заданий устанавливает преподаватель.
Задание № 1. Экспериментальное исследование зарядки и разрядки конденсатора большой ёмкости. 3.1. Экспериментальная часть
Измерения проводятся на лабораторной установке, состоящей из отдельного блока “R- С” и подключаемых к нему источника питания (выпрямителя) и цифрового вольтметра. Для измерений требуются также часы (секундомер) с отсчётом секунд и минут. На рисунке 2 показана принципиальная схема блока " R - С ", (аналогичная схеме рис.1). В блоке имеется высокоёмкостный металло-бумажный либо электролитический конденсатор, резистор в цепи зарядки с сопротивлением R1 и резисторы в цепи разрядки с сопротивлениями R02 и R03. . Величины сопротивлений R1, R02,rвн указаны на лабораторной установке и на л.13. Значения ёмкости С и сопротивления R03 требуется найти в опыте. Четырёхполюсный тумблер К-2 служит для переключения режимов зарядки и разрядки конденсатора. Двухполюсный тумблер К-3 позволяет подключать параллельно разрядному сопротивлению R02 второй резистор с сопротивлением R03. Двухполюсный тумблер К-1 служит для "закорачивания" конденсатора с целью его быстрой полной разрядки (при остаточном малом напряжении). Подключаемый к блоку вольтметр имеет внутреннее сопротивление =10,1 МОм, которое образует параллельное соединение с резисторами R02 и R03 при разрядке конденсатора, определяющее полную величину разрядного сопротивления. Обозначения тумблеров К1, К2, и КЗ даны на лицевой панели блока " R -C" с указанием их позиционных положений для разных режимов. На лицевой панели обозначены также клеммы для подключения выпрямителя и вольтметра. 3.2. Измерения 3.2.1. Присоедините к сети с напряжением ~220 В выпрямитель и вольтметр (последний – в режиме измерения постоянного напряжения), включите выпрямитель тумблером на его панели – загорится сигнальная лампочка. После прогрева выпрямителя в течение 5 мин измерьте и занесите в протокол напряжение Uвх на клеммах выпрямителя с надписью 12 В. 3.2.2. Выключите выпрямитель и подключите соединительные провода от выпрямителя и вольтметра к соответствующим клеммам блока “R – C”. 3.2.3. Установите тумблер К1 блока “R – C” в положение "Вкл". 3.2.4. Установите тумблер К2 в нейтральное положение и включите выпрямитель. 3.2.5. Переключите тумблер К2 в положение "ЗАРЯД" и одновременно включите секундомер. Через каждые 30 сек. (т.е. 0,5 мин), не выключая секундомер, заносите в табл.1- 1 значения напряжений на конденсаторе в процессе его зарядки в течение 15 мин.
Таблица 1–1
Здесь в первом столбце табл. 1-1 указано, что в начальный момент включения секундомера ( 3.2.6. Оставляя тумблер К2 в положении "ЗАРЯД", установите тумблер КЗ в положение “R2”, выключите и обнулите секундомер. 3.2.7. Переключите тумблер К2 в положение "РАЗРЯД" и одновременно включите секундомер. В этот же момент времени зафиксируйте значение напряжения на конденсаторе U0c и занесите его в табл. 2-1. Следующие значения напряжений на конденсаторе в процессе его разрядки заносите в табл. 2-1 через каждые 30 сек. в течение 10÷12 минут, после чего отключите и обнулите секундомер.
Таблица 2-1
Здесь в первом столбце табл. 2-1 указано, что в начальный момент включения секундомера ( (10 - 10,2) В. 3.2.8. Установите тумблер К2 в нейтральное положение и затем на короткое время выключите тумблер К1 с целью полной разрядки конденсатора. 3.2.9. Установите тумблер К1 в положение "ВКЛ" и выполните снова 3.210. Оставляя тумблер К2 в положении "ЗАРЯД", установите тумблер КЗ в положение “R3”. 3.2.11. Выполните снова разрядку конденсатора в соответствии с п.7, результаты заносите в табл.2-2 (по форме табл. 2-1). 3.2.12. По окончании измерений выключите выпрямитель и отключите приборы от сети ~220 В. Тумблер К2 блока “R – C” установите в нейтральное положение и выключите тумблер К1. Этим завершаются прямые измерения в задании № 1.
3.3. Обработка результатов
3.3.1. На миллиметровой бумаге формата АЗ постройте графические зависимости от времени для напряжения на конденсаторе в процессах его зарядки и разрядки. Все графики постройте на одном листе; на горизонтальной оси укажите время (мин.), на вертикальной оси - напряжение (В). Графики отметьте номерами: 1- зарядка; 2 - разрядка на сопротивление R2; 3 - разрядка на сопротивление R3 . 3.3.2. С помощью построенных графиков найдите неизвестные ёмкость конденсатора С и сопротивление R03 : а) ёмкость С определяется с помощью графика №2 при разрядке на сопротивление R2, величина которого определяется формулой (22а). Вычислив Rразр= R2 , необходимо затем на графике определить время релаксации Величина неизвестной ёмкости равна: Выполните проверку размерности, т.е. покажите, что в системе единиц СИ размерность ёмкости Ф (Фарада) соответствует отношению: Ф = сек/Ом. б) сопротивление R03 измеряется с помощью графика №3 при разрядке на сопротивление R3, величина которого определяется формулой, аналогичной (22а), но при условии, что параллельно резисторам с сопротивлениями R02 и Требуется на графике №3 определить время релаксации при разрядке При известных значениях R3 , R02 и 3.3.3. С помощью формулы (20) вычислите 3.3.4. Кроме п.п. 1-3, при обработке результатов - по указанию преподавателя - возможны дополнительные задания: а) с помощью формулы (19) при известных значениях ёмкости С б) результаты расчётов по разрядке конденсатора представить Для определения ёмкости С следует формулу (21а) преобразовать к виду:
где U02 - начальное напряжение при разрядке конденсатора на сопротивление R2 . Логарифмируя (3-1), получим:
Введём обозначение:
Тогда:
Значения Х2 легко вычисляются с помощью данных табл.2-1 для любого момента времени в процессе разрядки конденсатора. Необходимо вычислить 10 значений Х2 для 10 моментов времени и затем с помощью формулы (3-4) определить значения С и рассчитать среднюю величину ёмкости конденсатора. При расчётах время подставляется в секундах, сопротивление - в 0м. Погрешность (доверительный интервал) для величины С вычисляется по указанию преподавателя. Формулу (3-4) можно использовать также для построения линейного графика зависимости произведения График будет представлять собой прямую, проходящую через начало координат (см. рис.3):
Отношение абсциссы Для определения сопротивления R3 применяется аналогичный метод с учётом данных табл.2-2. Обозначая
получаем формулу:
где С - считается уже известной величиной и все значения X3 вычисляются для соответствующих моментов времени по данным табл.2-2 .
Задание № 2. Изучение импульсных переходных процессов в " r - с " контуре.
3.4. Экспериментальная часть
Лабораторная установка состоит из генератора типа ГЗ-Ш, магазина резисторов, магазина конденсаторов, осциллографа типа С1-69. Генератор типа ГЗ-Ш формирует на выходе периодические двуполярные прямоугольные импульсы в диапазоне частот от 20 Гц до 2 мГц. Настройка частоты осуществляется поворотом переключателя (на лицевой панели) с обозначенными коэффициентами умножения: 1; 10; 102; 103; 104 и затем - вращением шкалы точной настройки. Магазины резисторов и конденсаторов имеют на лицевой панели два ряда кнопок (клавиш). Верхний ряд определяет порядок величин, подключаемых к электрической цепи. Нижний рад определяет численное значение этих величин. На панели магазинов имеются также четыре гнезда для соединения с электрической цепью. Верхние гнезда, а также нижние соединены между собой. Осциллограф С1-69 представляет собой сложный по устройству прибор и требует специальных знаний для его настройки и эксплуатации. Этот осциллограф - двухлучевой, то есть в ЭЛТ (электроннолучевой трубке) прибора формируются два луча, управляемых электрическими сигналами, подающимися на два независимых входа. В настоящей работе при выполнении измерений на экране осциллографа один луч используется для "вычерчивания" линии нулевого отсчёта, второй луч "вычерчивает" на экране форму исследуемого импульса. На лицевой панели осциллографа имеются регуляторы яркости и фокусировки лучей; слева - расположен переключатель цены делений - [B/см] при вертикальном отклонении луча (для измерения амплитуд); справа - расположен переключатель цены делений - [Время/см] при горизонтальном смещении луча, изменяющий скорость развёртки по горизонтали и, соответственно, временные интервалы на горизонтальной оси шкалы экрана. Внимание: при измерениях на экране осциллографа яркость луча должна быть минимальной при оптимальной фокусировке. Излишняя яркость и плохая фокусировка приводят к уширению светового пятна на экране и, следовательно, к большой погрешности измерений амплитуд и интервалов времени. Для выполнения измерений необходимо собрать последовательно две схемы: контур дифференцирующей " R- С " цепочки и контур интегрирующей “ R - С " цепочки. Магазины резисторов и конденсаторов соединяются между собой и с генератором проводами с однополярными "наконечниками", вставляемыми в соответствующие гнезда. Осциллограф подключается коаксиальным кабелем. На рис. 4 и 5 показаны блок - схемы соединений. На рис.4 -для контура дифференцирующей цепочки, на рис.5 - для контура интегрирующей цепочки. Соответствующие принципиальные схемы и краткое описание даны в Приложении.
3.5. Измерения Внимание: настройка осциллографа и проведение измерений выполняются при участии инженера или преподавателя. 3.5.1. Включить в сеть с напряжением ~220 В генератор и осциллограф. 3.5.2. Отрегулировать яркость и фокусировку лучей на экране осциллографа. Совместить оба луча, вычерчивающих горизонтальные линии, на середине экрана (по высоте). 3.5.3. Подключить генератор к осциллографу (вход № 2). Устанавливая на генераторе, последовательно, частоты 5 кГц и 50 кГц, получить на экране устойчивое изображение периодических двуполярных прямоугольных импульсов. Для настройки скорости развёртки по горизонтали использовать интервалы времени с ценой деления: Переключателем цены деления по вертикали установить вертикальный размер импульса, равный ~ 3/4 высоты экрана. 3.5.4. Измерить амплитуду и длительность прямоугольного импульса с указанием в протоколе соответствующей цены деления 3.5.5. Собрать схему дифференцирующей цепочки (рис.4): а) установить на генераторе частоту - 50 кГц; б) набрать на магазине конденсаторов ёмкость в интервале: = (2÷10)∙102 Ом; в) получить на экране осциллографа устойчивое изображение г) измерить амплитуду и период следования импульсов. Занести 3.5.6. Опыт по п.5 повторить на частоте генератора 5 кГц для ёмкости С = =(5÷8)∙10-2 мкФ и сопротивления R = (6÷10)∙102 Oм (интервал развёртки =0,1 мс). 3.5.7. Собрать схему интегрирующей цепочки (рис.5): а) установить на генераторе частоту - 50 кГц; б) набрать на магазине конденсаторов ёмкость в интервале: =(2÷8) Oм; в)получить на экране осциллографа устойчивое изображение г) измерить амплитуду и длительность треугольных импульсов. Занести в протокол изображение импульсов на экране осциллографа. 3.5.8. На той же частоте 50 кГц получить на экране осциллографа изображение экспоненциальных импульсов. Для этого набрать на магазине конденсаторов ёмкость в интервале С = =(2÷5)∙10-2 мкФ при R =(2÷8) Ом (интервал развёртки 3.5.9. Опыты по п.7 повторить на частоте генератора 5 кГц для интервала развёртки при Треугольные импульсы получаются в интервалах: С =(5÷8)∙10-1 мкФ и R = =(2÷5)∙103 Oм. Экспоненциальные импульсы - в интервалах: С = (1÷4)∙10-2 мкФ и R = =(2÷5)∙103 Oм.
3.6. Обработка результатов
Обработка результатов задания №2 состоит в изображении схем импульсов с указанием их амплитуд и интервалов времени. Необходимо ознакомиться с материалом, данным в "Приложении".
ВОПРОСЫ ДЛЯ ПРОВЕРКИ (ПРИМЕРНЫЕ) 4.1. Понятие об электрической цепи. Типы электрических цепей. 4.2. Понятие об электрическом контуре. Правила Кирхгофа для электрического контура. 4.3. Понятие о переходных процессах в электрических цепях. Сущность классического метода описания переходных процессов. 4.4. Почему классический метод не применяется при сложной зависимости от времени входного напряжения на контуре? 4.5. Формулы для зависимости от времени напряжения на конденсаторе при его зарядке с постоянным входным напряжением и разрядке при отключённом входном напряжении. 4.6. Понятие времени релаксации при зарядке и разрядке конденсатора. 4.7. Как определяется неизвестная ёмкость конденсатора с учётом времени релаксации? 4.8. Понятие об импульсах в электрических цепях. Типы импульсов, параметры импульсов. 4.9. Понятие об интегрирующей и дифференцирующей цепочках. 4.10. Как на экране осциллографа получается графическое изображение формы импульса?
ЛИТЕРАТУРА
5.1. Г.В. Зевеке, II.А. Ионкин и др. Основы теории цепей. - М.: Энергия, 1975. - 741 с. 5.2. Л.Р. Нейман, К.С. Демирчян. Теоретические основы электротехники, т. 1,2. - л.: Энергоиздат, 1931. - 533 с; 415 с. 5.3. Л.Г. Толстов. Теория линейных электрических цепей. - М.: Высшая школа, 1973. - 272 с. 5.4. Ю.А. Исаков, В.С. Руденко и др. Промышленная электроника. - Киев.; Вища школа, 1975. - 323 с. 5.5. А.И. Ахиезер. Общая физики: Электрические и магнитные явления (справочное пособие). - Киев.:"Наукова Думка", 1981. - 171 с.
ПРИЛОЖЕНИЕ Общая характеристика импульсов и способов их формирования в электрических цепях 1. В электро - и радиотехнике импульсом называется кратковременное изменение напряжения (или тока) в электрической цепи от начального уровня до некоторого уровня Импульсы подразделяются на два основных типа: видеоимпульсы и радиоимпульсы. Видеоимпульс - это кратковременное изменение напряжения (или тока) при наличии постоянной (в среднем) составляющей напряжения (или тока). Графическое изображение в зависимости от времени, например, напряжения определяет геометрическую форму импульса; прямоугольную, трапецеидальную, экспоненциальную, треугольную (пилообразную) и т.д., см. рис.П-1. Импульсы могут иметь положительную либо отрицательную полярность.
Радиоимпульсом называется кратковременное появление высокочастотного синусоидального напряжения (или тока). Огибающая (геометрическая фигура) радиоимпульса имеет форму видеоимпульса. Частота синусоидального напряжения (или тока) называется несущей частотой. Для количественной оценки импульсов вводят специальные параметры; амплитуда Длительность импульсов обычно находится в пределах (10-9-1) с. В специальных случаях используются и более короткие импульсы. Под фронтами подразумеваются боковые стороны импульса: передняя и задняя. Мощность импульса определяется как энергия, выделяемая в цепи при прохождении импульса и отнесённая к его длительности. Импульсы могут быть единичными и периодическими. Для периодических импульсов вводят понятия: период повторения, частота и скважность импульсов. Периодом повторения импульсов называется интервал времени между началом двух ближайших однополярных импульсов. Частота повторения (или следования) - это величина, обратная периоду повторения. Скважностью называется безразмерная характеристика, равная отношению периода повторения к длительности импульса:
где 2. В практической электротехнике импульсы возникают в цепях В некоторых случаях такие импульсы могут иметь разрушительное действие. Простейшим примером является частое перегорание электроламп при выключении осветительной сети - в результате импульса тока, возникающего при кратковременном повышении напряжения (ЭДС самоиндукции). Формирование импульсов с различными параметрами необходимо для использования на практике (радио, телевидение, радиолокация и т.д.) и в научных исследованиях. Разработаны специальные схемы и устройства (генераторы импульсов), получившие широкое применение в практической и научной деятельности. Теоретический анализ импульсных схем сводится к определению переходных процессов в контурах электрических цепей и расчёту зависимостей от времени токов и напряжений. Для этого используются специальные методы, изучаемые в курсах электротехники и электроники. 3. Одними из простейших схем для формирования импульсов являются “R - C”, “R - L” и “R – L - C” контуры. “R - C” контур, используемый для формирования импульсов, обычно его называют “R - C” цепочкой (ячейкой). На контур подаётся входное напряжение Цепочка “R - C”, у которой напряжение на выходе пропорционально производной по времени от входного напряжения, называется дифференцирующей. Напряжение выхода при этом "снимается" с резистора. На рис.П-2а показана схема такой “R - C” цепочки. На рис. П-3а показан результат дифференцирования при подаче на вход прямоугольного двуполярного импульса напряжения. На выходе появляются "пикообразные" импульсы с напряжением, пропорциональным производной по времени от напряжения на фронтах (переднем и заднем) импульса, поступающего на вход контура. Значение
Цепочка “R - C” , у которой напряжение на выходе пропорционально интегралу по времени от входного напряжения, называется интегрирующей. Напряжение выхода при этом "снимается" с конденсатора. На рис.2б показана схема интегрирующей цепочки. На рис. П-3б показан результат (один из возможных) интегрирования при подаче на вход двуполярного прямоугольного импульса напряжения. Кроме показанного (пилообразного) импульса, на выходе могут быть получены импульсы экспоненциальной формы, а также прямоугольные импульсы с длительностью больше, чем у входного. Значение
В заключение отметим, что приведённые здесь формулы для напряжения на выходе не дают точного описания формы импульсов. Для такого расчёта следует найти передаточную функцию (коэффициент передачи) контура, которая вычисляется специальными (операторно - спектральными) методами.
|




 составим уравнения Кирхгофа для всей цепи, показанной на схеме рис.1. Обозначим заряд на конденсаторе q , токи в ветвях контуров -
составим уравнения Кирхгофа для всей цепи, показанной на схеме рис.1. Обозначим заряд на конденсаторе q , токи в ветвях контуров -  и для узла в т. В (или т. Д) и для двух контуров запишем три уравнения:
и для узла в т. В (или т. Д) и для двух контуров запишем три уравнения: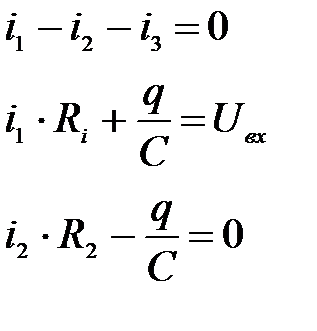 (1)
(1) (2)
(2) , (3)
, (3) . (3а)
. (3а) , т.к. ток в ветви В-Д определяется как производная по времени от величины заряда на обкладках конденсатора, и запишем (3) в виде дифференциального уравнения:
, т.к. ток в ветви В-Д определяется как производная по времени от величины заряда на обкладках конденсатора, и запишем (3) в виде дифференциального уравнения: (4)
(4) ).
). , позволяющая найти зависимость от времени для напряжения на конденсаторе
, позволяющая найти зависимость от времени для напряжения на конденсаторе  .
. (5)
(5) (6)
(6)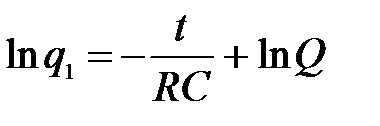 , (7)
, (7)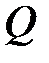 - константа, определяемая начальными условиями.
- константа, определяемая начальными условиями. (8)
(8) = 0 получаем:
= 0 получаем:  , где
, где  - начальная величина заряда на обкладках конденсатора.
- начальная величина заряда на обкладках конденсатора. (9)
(9) для уравнения (4) будем находить, используя формулу (8), считая, что величина коэффициента
для уравнения (4) будем находить, используя формулу (8), считая, что величина коэффициента  является некоторой (пока неизвестной) функцией времени.
является некоторой (пока неизвестной) функцией времени. , запишем отыскиваемое решение
, запишем отыскиваемое решение (10)
(10) (11)
(11)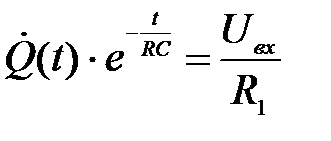 (12)
(12) (13)
(13) ), получаем для величины
), получаем для величины 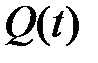
 (14)
(14) .
. (15)
(15) :
: (16)
(16) и
и  , получаем следующее выражение общего вида для зависимости напряжения на конденсаторе от времени:
, получаем следующее выражение общего вида для зависимости напряжения на конденсаторе от времени: (17)
(17) =0 и на входе подано постоянное напряжение
=0 и на входе подано постоянное напряжение  . При этом из (17) получаем следующее выражение, описывающее процесс зарядки конденсатора:
. При этом из (17) получаем следующее выражение, описывающее процесс зарядки конденсатора: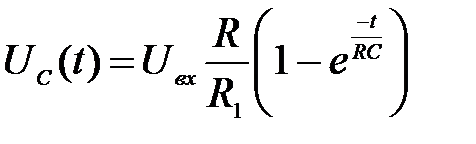 (18)
(18) , то легко доказать (применяя правило Лопиталя), что в формуле (За) получается:
, то легко доказать (применяя правило Лопиталя), что в формуле (За) получается: 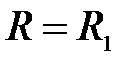 .
. (зарядное сопротивление),
(зарядное сопротивление), (18а)
(18а) , при этом
, при этом  . Например, для используемого в данной работе вольтметра типа В7-38 величина
. Например, для используемого в данной работе вольтметра типа В7-38 величина =10,1 МОм, сопротивление R1 , через которое заряжается конденсатор в опытах задания № I, равно R1
=10,1 МОм, сопротивление R1 , через которое заряжается конденсатор в опытах задания № I, равно R1  (1÷2) МОм. Следовательно, условие
(1÷2) МОм. Следовательно, условие  здесь не выполняется.
здесь не выполняется. , (19)
, (19) .
. формулы типа (18), (19) можно использовать для определения некоторых неизвестных параметров контура, например, R1, R2 или С. Следует также отметить, что согласно формуле (18) - при наличии включённого параллельно конденсатору ("шунтирующего") резистора с сопротивлением R2 - максимальное напряжение на конденсаторе при его зарядке (при
формулы типа (18), (19) можно использовать для определения некоторых неизвестных параметров контура, например, R1, R2 или С. Следует также отметить, что согласно формуле (18) - при наличии включённого параллельно конденсатору ("шунтирующего") резистора с сопротивлением R2 - максимальное напряжение на конденсаторе при его зарядке (при  ) оказывается меньше, чем входное (зарядное) напряжение, и равно:
) оказывается меньше, чем входное (зарядное) напряжение, и равно: (20)
(20) и
и  . При этом из (17) имеем следующее выражение, описывающее процесс разрядки конденсатора:
. При этом из (17) имеем следующее выражение, описывающее процесс разрядки конденсатора: (21)
(21) . Следовательно (применяя правило Лопиталя), из (За) получим: R1= R2 .
. Следовательно (применяя правило Лопиталя), из (За) получим: R1= R2 . (21а)
(21а)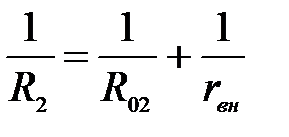 (22)
(22) (22а)
(22а) и называется временем релаксации для переходных процессов в R - С контуре при зарядке или разрядке конденсатора, соответственно.
и называется временем релаксации для переходных процессов в R - С контуре при зарядке или разрядке конденсатора, соответственно. , запишем формулу (18а) для момента времени
, запишем формулу (18а) для момента времени  :
: ;
;  зар –не множитель! (23)
зар –не множитель! (23) , т.е. в момент времени
, т.е. в момент времени  , запишем формулу (21а) для момента времени
, запишем формулу (21а) для момента времени 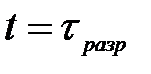
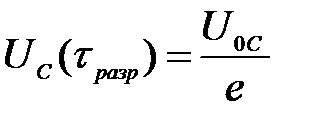 ;
;  разр – не множитель! (24)
разр – не множитель! (24) ;
; и отключённом входном напряжении.
и отключённом входном напряжении. можно, используя формулы (18) - (22а), определять величины неизвестных ёмкости конденсатора и сопротивлений резисторов.
можно, используя формулы (18) - (22а), определять величины неизвестных ёмкости конденсатора и сопротивлений резисторов.
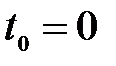 ) напряжение на конденсаторе
) напряжение на конденсаторе  .
.
 (на практике начальное напряжение при разрядке варьируется в пределах
(на практике начальное напряжение при разрядке варьируется в пределах 2 при разрядке (τразр при Uc). Для определения Uc используйте формулу (24).
2 при разрядке (τразр при Uc). Для определения Uc используйте формулу (24). . Учтите, что для расчётов время измеряется в секундах, сопротивление – в Ом.
. Учтите, что для расчётов время измеряется в секундах, сопротивление – в Ом.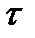 3, после чего определяется величина
3, после чего определяется величина  .
. и сравните полученный результат с величиной напряжения зарядки конденсатора за время, равное 15 мин. Учтите, что
и сравните полученный результат с величиной напряжения зарядки конденсатора за время, равное 15 мин. Учтите, что  - это значение напряжения на выпрямителе, найденное в п.1 раздела "Измерения".
- это значение напряжения на выпрямителе, найденное в п.1 раздела "Измерения". , (3-1)
, (3-1) (3-2)
(3-2)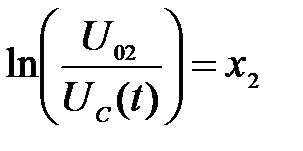 (3-3)
(3-3) (3-4)
(3-4) от времени. Для этого следует на горизонтальной оси указать время разрядки (сек), на вертикальной - значения
от времени. Для этого следует на горизонтальной оси указать время разрядки (сек), на вертикальной - значения  (Ом).
(Ом).
 к ординате
к ординате  определяет среднее значение ёмкости конденсатора.
определяет среднее значение ёмкости конденсатора. , (3-5)
, (3-5) , (3-6)
, (3-6)

 = 0,1 мс и
= 0,1 мс и  = 10 мкс.
= 10 мкс. и
и  (или
(или  ). При этом длительность импульса всегда меньше или сравнима с длительностью переходных процессов в этой цепи.
). При этом длительность импульса всегда меньше или сравнима с длительностью переходных процессов в этой цепи.
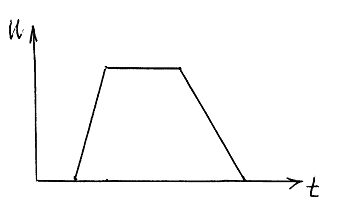


 , длительность импульса
, длительность импульса  , длительность переднего фронта
, длительность переднего фронта  , длительность среза (заднего фронта)
, длительность среза (заднего фронта) 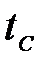 , мощность импульса
, мощность импульса  .
. ,
, - длительность паузы, т.е. интервала времени между окончанием и началом двух ближайших импульсов (см. рис. П-1).
- длительность паузы, т.е. интервала времени между окончанием и началом двух ближайших импульсов (см. рис. П-1). (постоянное или переменное), на выходе (т.е. на конденсаторе или резисторе) - появляется напряжение
(постоянное или переменное), на выходе (т.е. на конденсаторе или резисторе) - появляется напряжение 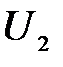 , зависящее от переходного процесса в контуре.
, зависящее от переходного процесса в контуре. при этом (приближённо) определяется формулой:
при этом (приближённо) определяется формулой:

