 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задание для интерполяции функций
Лабораторная работа по теме «Тема 1.3. Интерполяция функций»
Вопросы, подлежащие изучению 1.Постановка задач аппроксимации и интерполяции. 2.Основные понятия: интерполирующая и интерполируемая функции, условие интерполяции. Связь между числом узлов интерполяции и порядком интерполирующего многочлена. 3.Условие единственности решения задачи интерполирования. 4.Интерполяционный многочлен Лагранжа: назначение, область применения. 5.Методика выбора узлов интерполяции при использовании формул Лагранжа и Ньютона. 6.Способы оценки погрешностей интерполяции по формулам Лагранжа и Ньютона. Способы повышения точности интерполяции. 7.Интерполяционная формула Ньютона, область применения. 8.Конечные разности, их назначение и использование. Свойства конечных разностей. 9.Правило выбора начальных узлов интерполяции для формул Ньютона. 10.Практическое правило определения степени интерполяционного многочлена. 11.Сравнение интерполяционных формул Лагранжа и Ньютона. 12.Погрешность интерполяции. 13.Сплайн интерполяция.
Задание 1. Выбрать индивидуальное заданиеиз табл.1.3-1 и табл. 1.3-2 для решения задач интерполяции: · из табл. 1.3-1 выбираем значения параметров t1 и t2,а такжезначенияx=a (для построения многочлена Ньютона) и x=b (для построениямногочлена Лагранжа); · из табл. 1.3-2 в соответствии с методикой выбора узлов интерполяции по значению x=a выбираем узлы интерполяции (из отрезка [0.05;1.55] – область задания интерполируемой функции) и значения функции в этих узлах. Число узлов определяется заданной степенью интерполяционного многочлена в соответствии с п.2 и п.3. Следует обратить внимание, что: o если точка x=a расположена ближе к левому концу отрезка, выбираемого из табл.1.3-2, то для построения первой формулы Ньютона необходимо выбрать узлы o если точка x=a расположена ближе к правому концу отрезка, выбираемого из табл.1.3-2, то используют вторую формулу Ньютона и необходимо выбрать узлы o если точка x=a расположена примерно в середине таблицы, то следует выбрать ту формулу, которая обеспечит меньшую погрешность.
2. Выполнить линейную, квадратичную и кубическую интерполяцию функции · составить схему алгоритма и программу решения задачи интерполяции и провести контрольное тестирование на данных примера, разобранного в п. 5; · вычислить значение интерполирующего многочлена Ньютона в точке · провести оценку погрешности интерполяции по формулам практической оценки погрешности. 3. Построить интерполяционный многочлен второй степени (Ньютона или Лагранжа в зависимости от значения t2) в явном виде (ручной расчет). Вычислить значения построенного многочлена во всех выбранных узлах интерполяции. Сравнить полученные результаты с таблично заданными значениями.
Варианты задания Таблица 1.3-1
В табл. 1.3-1t1, t2 – способы аппроксимации функции в соответствии с п.2 и п.3 задания. Если в графе стоит 1, то использовать интерполяционный многочлен Ньютона, если 2, то интерполяционный многочлен Лагранжа.
Таблица 1.3-2
Например, выбор задания из табл.1.3-1 по номеру варианта (№10): 1.Выбрать метод (в графе t1 указано значение 2 – выполнить интерполяцию с использованием многочлена Лагранжа), далее выбрать из этой же строки номера узлов (23, 24, 26, 28, 29, 30), которым соответствуют значения аргумента и функции в 2.Из столбца t2 выбрать метод (1 – построить в явном виде интерполяционный многочлен Ньютона), выбрать из табл.1.3-2 узлы интерполяции в соответствии со значением Содержание отчета 1.Индивидуальное задание. Для многочленов Ньютона и многочлена Лагранжа указать последовательность выбранных узлов из предложенного диапазона 2.Линейная, квадратичная и кубическая интерполяция функции · схемы алгоритмов и программа интерполяции с результатами контрольного тестирования; · значения интерполирующего многочлена Ньютона в точке · значения погрешностей интерполяции по формулам практической оценки погрешности, результат которых необходимо записать в табл. 1.3-3. Таблица 1.3-3
3.Интерполяционный многочлен второй степени (Ньютона или Лагранжа в зависимости от значения t2) в явном виде (вручную) и значения построенного многочлена во всех выбранных узлах интерполяции, которые необходимо записать в табл. 1.3-4; сравнить полученные результаты с таблично заданными значениями. Таблица 1.3-4
Пример выполнения задания Задание для интерполяции функций функция y=f(x), заданная таблично значениями в узлах интерполяции:
· вычислим значение многочлена Ньютона в точке x=a=0.57 и значение многочлена Лагранжа в точке x=b= 0.62: · для вычисления значения интерполирующей функции в точке x=a=0.57 методом Ньютона выберем узлы интерполяции х0=0.55, х1=0.60, х2=0.65, х3=0.70(x0=0.55– ближайший к точкех=а=0.57узел слева); · для вычисления значения интерполирующей функции в точке x=b=0.62 методом Лагранжа выберем номера узлов интерполяции 1, 2, 3, 4, что соответствует значениям узлов х0=0.55, х1=0.60, х2=0.65, х3=0.70(из указанного диапазона узлов).
2. Линейная, квадратичная и кубическая интерполяция«расчетом на ПК»: · схемы алгоритмов представлены на рис. 1.3.2-1, 1.3.2-2 и рис. 1.3.3-1 в [2], а программы студенты должны написать самостоятельно; · значение полинома в заданной точке.
Для построения интерполяционного многочлена Ньютона воспользуемся первой интерполяционной формулой Ньютона, так как точка интерполяции a =0.57 находится в начале таблицы значений выбранных узлов интерполяции (отрезок[0.50;0.75]). Ближайший к точке а узел слева х=0.55, поэтому полагаем Для линейной интерполяции следует взять узлы Для квадратичной и кубической интерполяции выберем соответственно следующие последовательности узлов:
(число узлов равно n+1, где n – порядок многочлена). Для выбранной последовательности узлов: • построить таблицу конечных разностей;
• вычислить значение интерполирующего многочлена Ньютона в точке a=0.57, воспользовавшись формулой 1.3.3-6 в [2] при
Значение интерполирующего многочлена Ньютона при n+1=2 (линейная интерполяция):
Аналогично вычисляются значения • при n+1=3 (квадратичная интерполяция): Р2(0.57)=1.08446 , • при n+1=4 (кубическая интерполяция): Р3(0.57)=1.08438. В случае, если точка интерполяции находится в конце таблицы, на которой задана функция y=f(x), интерполирование проводится по второй интерполяционной формуле Ньютона1.3.3-9 в [2] при Например, если задана точка интерполяцииа=0.73, то для линейной интерполяции в этом случае следует взять узлы:xn=0.75, xn-1=0.70,для квадратичной – узлы: xn=0.75, xn-1=0.70, xn-2=0.65, для кубической - xn=0.75, xn-1=0.70, xn-2=0.65, xn=3=0.60. Тогда Если точка интерполяции находится в середине таблицы, то выбор интерполяционной формулы Ньютона производится исходя из значения величины q. Например, если x=a=0.58, то для построения квадратичного полинома (n+1=3) лучше выбрать узлы xn=0.60, xn-1=0.55, xn-2=0.50,так как при этом величина q будет меньше(q=-0.4). (Для сравнения: если выбрать узлы x0=0.55, x1=0.60, x2=0.65, то q=0.6). Для построения интерполяционного многочлена Лагранжа воспользуемся формулой Для обеспечения большей точности интерполяции перенумеруем узлы интерполяции: выберем узел
Вычислим значение интерполирующего многочлена Лагранжа в точке b=0.62. При n+1=1 (линейная интерполяция) значение интерполирующего полинома будет следующим:
Проведя аналогичные вычисления, получим значения интерполирующего полинома: · при n+1=2 (квадратичная интерполяция) - · при n+1=3(кубическая интерполяция) -
Вычислим погрешность интерполяции по формулам практической оценки погрешности. Погрешность первой формулы Ньютона оценим по 1.3.3-13 в [2].
Для линейной интерполяции: Для квадратичной интерполяции: Для кубической интерполяции:
Анализируя полученные значения погрешностей, можно сделать вывод, что интерполируемая функция близка к квадратичной, так как конечные разности третьего порядка значительно различаются, а Оценку погрешности многочлена Лагранжа произведем по формуле:
Исходными данными для программной реализации являются таблично заданная функция y=f(x) и значения x=aилиx=b. (Заметим, что при составлении программы алгоритма следует предусмотреть вывод значений конечных разностей). Результаты интерполяции и оценки погрешности следует записать в табл.1.3-3:
3. Построение интерполяционных многочленов второй степенив явном виде («ручной расчет») Для построения интерполяционных многочленов, помимо известных из [2] формул,можно использовать формулы1.3.2-6 и 1.3.3-4 из [2]. Построенные квадратичные интерполяционные полиномы Ньютона (для выбранных узлов) и Лагранжа (для выбранных узлов) имеют вид: P2(x)= 2.54 x2 + 0.053x + 0.229, L2(x) = 2.54 x2 + 0.053x + 0.229. Выражения для полиномов совпали, т.к. для построения обоих многочленов были выбраны одинаковые узлы. Вычислим значения построенного многочлена в выбранных узлах интерполяции и занесем в табл.1.3-4 и для сравнения туда же занесем таблично заданные значения исходной функции:
1.3.6. Контрольные вопросы по теме «Тема 1.3. Интерполяция функций»
|



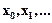 (
(  - ближайший к точке x=a узел слева);
- ближайший к точке x=a узел слева); (xn – ближайший к точке x=a узел справа);
(xn – ближайший к точке x=a узел справа);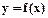 , заданной таблично (табл.1.3-2), указанным в табл.1.3-1 методом (значение t1) «расчет на ПК»:
, заданной таблично (табл.1.3-2), указанным в табл.1.3-1 методом (значение t1) «расчет на ПК»: ; для многочлена Лагранжа в точке
; для многочлена Лагранжа в точке  ;
; (a=1.12).
(a=1.12). для первой формулы Ньютона,
для первой формулы Ньютона, 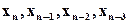 - для второй формулы Ньютона,
- для второй формулы Ньютона,  - для формулы Лагранжа.
- для формулы Лагранжа. , заданной таблично (табл. 1.3-2), указанным в табл. 1.3-1 методом (значение t1) «расчета на ПК»:
, заданной таблично (табл. 1.3-2), указанным в табл. 1.3-1 методом (значение t1) «расчета на ПК»:


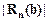




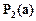




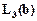


 .
. и
и  .
. ;
;






 .
. , xn – ближайший к точке х узел справа.
, xn – ближайший к точке х узел справа.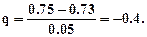
 (ближайший к точке b=0.62), далее выбираем узлы по возможности симметрично относительно точки интерполяции b=0.62:
(ближайший к точке b=0.62), далее выбираем узлы по возможности симметрично относительно точки интерполяции b=0.62:






 .
. .
. .
.
 .
. ,
,  ,
,  ,где b=0.62.
,где b=0.62.


 |
|