ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Пример выполнения задания. 12
ВАРИАНТЫ ЗАДАНИЙ ДЛЯ ВЫПОЛНЕНИЯ КОНТРОЛЬНОЙ РАБОТЫ Для студентов 2 курса экономического факультета (заочное образование) (дисциплина «Эконометрика)
Выбор варианта контрольной работы. Работа включает в себя выполнение двух задач: - парная регрессия и корреляция - множественная регрессия и корреляция
Выбор варианта задания осуществляется следующим образом (см. таблицу «выбор варианта контрольной работы).
Пример выбора варианта задания: Студент: Малахов Иван Петрович Шифр зачетной книжки: 20119
Вариант задания контрольной работы 9,4(I задача- вариант № 9; II задача – вариант № 4)
Краткие теоретические сведения, примеры выполнения заданий и варианты заданий изложены ниже.
1. Парная регрессия и корреляция Теоретическая часть. Линейная регрессия сводится к нахождению уравнения вида
Уравнение вида Построение линейной регрессии сводится к оценке ее параметров – a и b. Уравнение простой регрессии характеризует связь между двумя переменными, которая проявляется как некоторая закономерность лишь в среднем по совокупности в целом наблюдаемых данных. Каждую пару наблюдений xi ,yi можно представить в виде точки на плоскости ху. Такое графическое построение называется полем корреляции. В этом случае наилучшей считается функция, график которой проходит через наибольшее количество точек или как можно ближе к ним.
В каждом из наблюдений величину случайной компоненты можно определить как разность между фактическим значением результата и рассчитанным по уравнению регрессии:
Параметр b называют коэффициентом регрессии, рассчитывается по формуле:
Его величина показывает, насколько в среднем изменяется значение результативного признака при изменении факторного на единицу. Параметр а оценивается по следующей формуле:
Пример выполнения задания. В таблице 1 приведены условные данные, характеризующие среднедушевой прожиточный минимум в день на одного трудоспособного, руб., х и среднедневную заработную плату Таблица.1
Требуется: 1.Построить линейное уравнение парной регрессии 2.Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. 3.Оценить статистическую значимость параметров регрессии и корреляции с помощью 4.Выполнить прогноз заработной платы 5.Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. 6.На одном графике построить исходные данные и теоретическую прямую. Решение 1.Вспомогательные дополнительные расчеты для определения параметров уравнения линейной регрессии представлены в таблице 2. Таблица 2 – Дополнительные расчеты
;
. Получено уравнение регрессии:
С увеличением среднедушевого прожиточного минимума на 1 руб. среднедневная заработная плата должна возрасти в среднем на 0,92 руб. 2.Тесноту линейной связи оценит коэффициент корреляции:
Это означает, что 52% вариации заработной платы ( Качество модели определяет средняя ошибка аппроксимации:
где Качество построенной модели оценивается как хорошее, так как 3.Оценку значимости уравнения регрессии в целом проведем с помощью
Табличное значение критерия при пятипроцентном уровне значимости и степенях свободы Оценку статистической значимости параметров регрессии проведем с помощью Табличное значение Определим случайные ошибки
Тогда
Фактические значения
поэтому параметры Рассчитаем доверительные интервалы для параметров регрессии
Доверительные интервалы
Анализ верхней и нижней границ доверительных интервалов приводит к выводу о том, что с вероятностью 4.Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение прожиточного минимума составит: 5.Ошибка прогноза составит:
Предельная ошибка прогноза, которая в
Доверительный интервал прогноза:
Выполненный прогноз среднемесячной заработной платы является надежным ( 6.В заключение решения задачи построим на одном графике исходные данные и теоретическую прямую (рис. D.1):
Рис. 1. Варианты индивидуальных заданий по теме «Парная регрессия и корреляция» Задание 1.Построить линейное уравнение парной регрессии 2.Рассчитать линейный коэффициент парной корреляции и среднюю ошибку аппроксимации. 3.Оценить статистическую значимость параметров регрессии и корреляции с помощью 4.Выполнить прогноз заработной платы - 115% от среднего уровня; - 130% от среднего уровня. 5.Оценить точность прогноза, рассчитав ошибку прогноза и его доверительный интервал. 6.На одном графике построить исходные данные и теоретическую прямую. Вариант 1 Таблица 3 – Исходные данные для построения уравнения линейной регрессии
Вариант 2 Таблица 4 – Исходные данные для построения уравнения линейной регрессии
Вариант 3 Таблица 5 – Исходные данные для построения уравнения линейной регрессии
Вариант 4 Таблица 6 – Исходные данные для построения уравнения линейной регрессии
Вариант 5 Таблица 7 – Исходные данные для построения уравнения линейной регрессии
Вариант 6 Таблица 8 – Исходные данные для построения уравнения линейной регрессии
Вариант 7 Таблица 9 – Исходные данные для построения уравнения линейной регрессии
Вариант 8 Таблица 10 – Исходные данные для построения уравнения линейной регрессии
Вариант 9 Таблица 11 – Исходные данные для построения уравнения линейной регрессии
Вариант 10 Таблица 12 – Исходные данные для построения уравнения линейной регрессии
Вопросы для самоконтроля: 1. По каким вычислениям можно судить о значимости модели в целом? 2. Зачем необходимо рассчитывать t-критерий Стьюдента? 3. Зачем необходимо оценивать интервалы прогноза по линейному уравнению регрессии? 4. В каких пределах должна находиться ошибка аппроксимации, чтобы можно было сделать вывод о хорошем подборе модели к исходным данным?
12 |



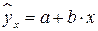 или
или  .
. позволяет по заданным значениям фактора x находить теоретические значения результативного признака y, подставляя в него фактические значения фактора x.
позволяет по заданным значениям фактора x находить теоретические значения результативного признака y, подставляя в него фактические значения фактора x.





 -критерия Фишера и
-критерия Фишера и  -критерия Стьюдента.
-критерия Стьюдента.












 .
.
 не превышает 8-10%.
не превышает 8-10%.
 и
и  составляет
составляет  . Так как Fфакт = 10,83> Fтабл = 4,96, то уравнение регрессии признается статистически значимым. Табличное значение критерия Фишера можно определить использую функцию FРАСПОБР.
. Так как Fфакт = 10,83> Fтабл = 4,96, то уравнение регрессии признается статистически значимым. Табличное значение критерия Фишера можно определить использую функцию FРАСПОБР. и
и  составит
составит  .
. ,
, 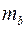 ,
,  :
: ;
; ;
; .
.


 ;
; 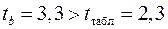 ;
;  ,
, ,
,  и
и  являются статистически значимыми для уравнения регрессии.
являются статистически значимыми для уравнения регрессии. ;
;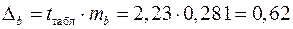 .
.
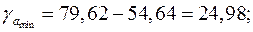




 параметры
параметры  руб., тогда прогнозное значение заработной платы составит:
руб., тогда прогнозное значение заработной платы составит:  руб.
руб. .
. случаев не будет превышена, составит:
случаев не будет превышена, составит: .
.
 руб.;
руб.; руб.
руб. ) и находится в пределах от 131,66 руб. до 190,62 руб.
) и находится в пределах от 131,66 руб. до 190,62 руб.