 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Метод симметричных составляющих 12
Лабораторная работа № 4 Переходный процесс при несимметричном коротком замыкании в электрической сети, питающейся от источника практически бесконечной мощности Продолжительность работы:4 часа. Цель работы:Изучение переходного процесса в электрической сети при нессиметричном коротком замыкании. Программа изучения переходных процессов при несимметричном коротком замыкании: 1. Ознакомиться с теоретической частью. 2. Ознакомиться с конструкцией стенда. 3. Ознакомится с порядком выполнения работы. 4. Собрать схему лабораторной работы согласно указаниям. 5. Провести необходимые испытания. 6. Составить отчет по проделанной работе. Краткие теоретические сведения: Несимметричные переходные процессы в электрических системах Несимметричные режимы возникают вследствие несимметричных коротких замыканий или обрыва одной-двух фаз линии. В первом случае в электрической сети появляется поперечная несимметрия, во втором – продольная. Строгий математический анализ переходных процессов при несимметрии затруднён тем, что в электрических машинах возникает пульсирующее магнитное поле ротора, которое образует полный спектр высших гармонических составляющих тока. Замена координатных осей А, В, С на систему d, q, 0 не освобождает дифференциальные уравнения от периодических коэффициентов. Поэтому в большинстве практических расчётов учитывается лишь основная гармоника токов или напряжений. Только при таком ограничении возможно использование метода симметричных составляющих, который наиболее часто применяется для анализа несимметричных КЗ [2, глава 6]. Метод симметричных составляющих Метод симметричных составляющих базируется на математической теории многофазных электрических систем при неодинаковых условиях работы фаз. Математическое обоснование метода было разработано К. Фортескью (С. L. Fortescue), а затем Р. Эвансом и К. Вагнером (R. Evans и С. Wagner), которые применили его для решения задач, возникающих при анализе несимметричных КЗ. Сформулируем основные положения метода симметричных составляющих. 1.Любую несимметричную систему токов можно разложить на три симметричные, называемые системами прямой, обратной и нулевой последовательностей. Эти системы получили название «симметричные составляющие». Предполагается, что они одновременно циркулируют в рассматриваемой сети в несимметричном режиме. Симметричная система токов прямой последовательности (рис. 1.42, а) представляет собой три одинаковых по величине вектора, расположенных под углом 120°, вращающихся против часовой стрелки так, что соблюдается нормальное чередование фаз: А – В – С. Соотношения между фазными значениями устанавливаются с помощью оператора
Рис. 4.1. Система токов прямой (а), обратной (б) и нулевой (в) последовательностей. Любой из трёх одинаковых векторов единичной длины имеет аргумент, равный 120°. Если некоторый вектор, например IА1 , умножить на a , то это означает повернуть IА1 на 120° против часовой стрелки. С помощью оператора a можно выразить токи фаз В и С через ток фазы А:
Симметричная система токов обратной последовательности (рис. 4.1, б) представляет собой три одинаковых по величине вектора, расположенных под углом 120° и вращающихся против часовой стрёлки так, что соблюдается обратное чередование фаз: А–С–В. При этом токи фаз В и С связаны с током фазы А следующим образом:
Симметричная система токов нулевой последовательности (рис. 4.2, в) существенно отличается от прямой и обратной. Она представляет собой систему трёх переменных токов, совпадающих по фазе и имеющих одинаковую амплитуду. Эти токи являются, по существу, разветвлением однофазного тока, для которого три провода трёхфазной цепи составляют один прямой провод, а обратным служит земля или четвертый (нулевой) провод. Появление токов нулевой последовательности в сети означает возникновение в ней несимметричного замыкания на землю. Рассматриваемая несимметричная система токов допускает только одно разложение на симметричные составляющие. Действительно, представив ток каждой фазы через его симметричные составляющие, получим:
Если IА , IВ , IС заданы, то искомыми являются три величины
Все соотношения для симметричных составляющих токов справедливы и для напряжений. Рассмотрим разложение на составляющие несимметричной системы токов (рис. 4.2, а).
Рис. 4.2. Разложение несимметричной системы токов на симметричные составляющие С помощью геометрических построений, соответствующих выражениям (4.8) – (4.10), найдём ток нулевой, прямой и обратной последовательностей (рис. 4.2, б–г). Если сложить симметричные составляющие в соответствии с выражениями (4.5) – (4.7), то получим исходную систему. 2.В трёхфазной цепи в месте КЗ наряду с напряжениями прямой последовательности возникают напряжения обратной и нулевой последовательностей. В ветвях схемы вместе с токами прямой последовательности начинают циркулировать токи обратной и нулевой последовательностей. 3.В симметричных электрических системах токи и напряжения схем отдельных последовательностей могут рассматриваться независимо друг от друга и быть связаны между собой законами Ома и Кирхгофа. Если какой-либо элемент цепи симметричен и при протекании по нему токов I1, I2, I0 обладает некоторыми сопротивлениями Z1 , Z2 , Z0 , то симметричные составляющие падения напряжения в этом элементе будут равны
4.Элементы трёхфазной сети для токов прямой, обратной и нулевой последовательностей имеют неодинаковые сопротивления. ЭДС генераторов симметричны, т.е. не содержат обратной и нулевой составляющих. Отсюда следует, что: а) в электрических системах существуют только ЭДС прямой последовательности; б) токи обратной и нулевой последовательностей определяются только напряжениями в точке КЗ. 5.Между системами трёх симметричных составляющих всегда существует связь, задаваемая условиями короткого замыкания. Эта связь легко устанавливается путём перевода граничных условий короткого замыкания, заданных через действительные токи и напряжения, в условия, заданные через симметричные составляющие. Подробнее с теорией о методе симметричных составляющих можно ознакомится, используя пособия указанные в списке литературы [2, глава 6].
12 |





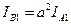 (4.1)
(4.1) (4.2)
(4.2) (4.3)
(4.3) (4.4)
(4.4) (4.5)
(4.5) (4.6)
(4.6) (4.7)
(4.7) . Они определяются тремя линейными уравнениями, которые допускают только одно решение:
. Они определяются тремя линейными уравнениями, которые допускают только одно решение: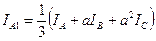 (4.8)
(4.8) (4.9)
(4.9) (4.10)
(4.10)
 (4.14)
(4.14)