 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Нелинейная задача оптимизации производственной деятельности фирмы
Пусть производственная фирма выпускает один продукт, либо несколько продуктов в заданной пропорции. Тогда ее выпуск за заданный плановый период – это количество единиц продукта одного вида, либо число многономенклатурных агрегатов. Пусть для выпуска продукции фирмой используются два вида ресурсов. И величина выпуска описывается нелинейной двухфакторной производственной функцией Кобба-Дугласа:
Здесь По своему содержательному смыслу количества используемых ресурсов – неотрицательны. Это означает выполнение неравенств
Пусть известны цена единицы первого ресурса
где Эти затраты не могут превышать максимально возможного за плановый период общего объема издержек
Пусть известна цена единицы производимого продукта
Эту величину надо максимизировать. Собирая все вместе, математическую постановку нелинейной задачи оптимизации производственной деятельности фирмы запишем в виде:
при ограничениях
Укажем способ решения этой задачи с помощью инструмента Поиск решения. Для примера рассмотрим задачу, исходные данные которой приведены в таблице 5.1.
Таблица 5.1
Математическая запись данного примера имеет вид:
при ограничениях
Рассмотрим три этапа решения данного примера с помощью инструмента Поиск решения.
Этап 1. Введем исходные данные нелинейной задачи оптимизации производственной деятельности фирмы. В соответствующие ячейки введем координаты начальной точки, формулы для вычисления суммарных затрат на использование ресурсов
Рисунок 5.1. Входные данные примера нелинейной задачи оптимизации производственной деятельности фирмы
На рисунке 5.1 видно, что исходные данные примера расположены в горизонтальном массиве, элементы которого введены в ячейки диапазона B39:H39. Непосредственно над каждой ячейкой, расположенной в этом диапазоне, написано обозначение того входного параметра, который содержится в этой ячейке. Для переменных компонент В ячейку D42 введена формула для вычисления суммарных затрат на использование ресурсов В ячейке E42 содержится формула для вычисления значения производственной функции Кобба-Дугласа В ячейку F42 введена формула для вычисления значения прибыли
Этап 2. Вызовем инструмент Поиск решения и введем условия задачи. После выполнения указанных выше действий появится диалоговое окно Поиск решения, показанное на рисунке 5.2.
Рисунок 5.2. Диалоговое окно Поиск решения для примера нелинейной задачи оптимизации производственной деятельности фирмы
В пункте 3 подробно описано, как можно задать условия задачи в диалоговом окне Поиск решения. Далее, после щелчка по кнопке Параметры, переходим в диалоговое окно Параметры поиска решения. Установим в нем значения параметров, показанные на рисунке 5.3.
Рисунок 5.3. Диалоговое окно Параметры поиска решения для примера нелинейной задачи оптимизации производственной деятельности фирмы
На рисунке 5.3 видно, что флажок установлен только для параметра Неотрицательны значения. Флажок для параметра Линейная модель устанавливать нельзя, потому что решается нелинейная задача. После окончания введения параметров щелкнем по кнопке OK и вернемся в диалоговое окно Поиск решения.
Этап 3. Решение задачи инструментом Поиск решения. Для решения нашего примера инструментом Поиск решения, надо в диалоговом окне Поиск решения, показанном на рисунке 5.2, щелкнуть по кнопке Выполнить. После завершения работы инструмента Поиск решения появится диалоговое окно Результаты поиска решения, изображенное на рисунке 3.5. В этом окне надо поставить флажок на опцию Сохранить найденное решениеи затем щелкнуть кнопку OK. Результат решения нашего примера приведен на рисунке 5.4.
Рисунок 5.4. Результат решения примера нелинейной задачи оптимизации производственной деятельности фирмы
Этап 4. Анализ полученного решения. Сравнивая значения ячеек D39 и D42 видим, что суммарные затраты на использование ресурсов в течение планового периода в нашем примере являются максимально возможными.
|
.
- это количество используемых в течение планового периода единиц первого ресурса, а 
- количество единиц второго ресурса. Обычно в качестве первого ресурса рассматривается капитал, а в качестве второго – труд. Положительный коэффициент 
равен объему выпуска продукции при единичных затратах ресурсов. Эластичность выпуска по первому ресурсу 
удовлетворяет неравенствам 
. И эластичность выпуска по второму ресурсу 
удовлетворяет тем же неравенствам.
и цена единицы второго ресурса 
. Тогда суммарные затраты на использование ресурсов в течение планового периода равны
,
и 
– двумерные векторы, а 
– их скалярное произведение.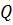
, что означает справедливость неравенства
.
. Тогда прибыль (чистый доход) фирмы за плановый период равна
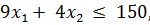
и значения прибыли 
. Для рассматриваемого примера это можно сделать, например, следующим образом.
, использован горизонтальный массив, состоящий из двух элементов, которые содержатся в ячейках диапазона B42:C42. Экспериментально замечено, что использовать в качестве начальных значений этих компонент нулевые значения нельзя. Инструмент Поиск решения принимает начальную точку (0,0) за оптимальное решение в тех задачах, в которых она не является даже точкой локального максимума. В качестве начальных точек рекомендуется выбирать точки с одинаковыми и положительными компонентами. В данном примере в качестве начальной точки выбрана точка (1,1).
