 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Описание установки и метода измерений
КОЛЕБАНИЯ И ВОЛНЫ
Методические указания к лабораторным работам № 20, 21. 23, 25, 26, 27 для студентов 1 - 2 курсов всех специальностей
НОВОСИБИРСК
Лабораторная работа № 23
Свободные электромагнитные колебания
Цель работы
Экспериментально и теоретически установить зависимости периода колебаний Т, логарифмического декремента затухания l, добротности Q от параметров контура (R, L, C).
Методические указания
Рассмотрим колебательный контур (рис.1). Сопротивление всякого реального контура не равно нулю. Вследствие этого, энергия, первоначально запасенная в контуре, непрерывно расходуется на выделение джоулева тепла в резисторе R (если он есть), в катушке индуктивности и в конденсаторе, так что амплитуда электромагнитных колебаний постепенно уменьшается и в конце концов колебания прекращаются. Таким образом, в реальном контуре свободные колебания являются затухающими [ 1, с. 521 ]. Чтобы найти уравнение колебаний в контуре, используем закон Ома для участка цепи 1 - 3 -2 [ 2, с. 103 ]. IR = (j1 - j2) + e12 , (1) где e12 = eS. Выражая в (1) ток I, разность потенциалов (j1 - j2) и ЭДС самоиндукции eS через заряд конденсатора q и параметры контура, получим дифференциальное уравнение затухающих колебаний в контуре [ 2, с. 255 - 258 ], [ 3, с. 369 - 372 ].
Вводя коэффициент затухания
и обозначая
где
Если затухание мало, т.е. d2 <
где
Таким образом, при замыкании заряженного конденсатора на цепь из последовательно соединенных L и R, заряд на обкладках конденсатора изменяется с течением времени согласно выражению (6). Частота затухающих колебаний w определяется параметрами контура R, L, С, причем w < wо. Если активное сопротивление контура R = 0, то w = wо. Затухающие колебания не являются, строго говоря, периодическим процессом, так как изменяющаяся со временем величина, например, заряд, не принимает одинакового значения через промежуток времени, равный периоду колебаний Т. Тем не менее, в рассматриваемом случае, когда затухание мало, можно говорить о затухающих колебаниях, как о периодических, амплитуда которых Период затухающих колебаний Т определится по формуле
При малом затухании период затухающих колебаний можно приближенно считать равным периоду незатухающих
Напряжение на конденсаторе Uс, сила тока в контуре I, напряжение на катушке индуктивности UL так же, как и заряд совершают затухающие колебания, поскольку они связаны с зарядом.
где Для количественной характеристики затухания вводят логарифмический декремент затухания
Под
При малом затухании
С увеличением сопротивления контура коэффициент затухания растет, частота w уменьшается (7), а период затухающих колебаний увеличивается. При некотором сопротивлении контура период становится равным бесконечности, а частота колебаний обращается в нуль (Т = ¥, w = 0). В этом случае в контуре вместо колебаний происходит апериодический разряд конденсатора (рис.3, кривые а, б).
Сопротивление контура, при котором колебательный процесс переходит в апериодический, называется критическим Rкрит.. Величину критического сопротивления определяют из условия
Для определения качества контура как колебательной системы часто используется, особенно в радиотехнике, особый параметр - добротность контура
Описание установки и метода измерений Свободные электромагнитные колебания можно получить в цепи, собранной по схеме рис.4. Измерительная установка состоит из следующих основных узлов: генератора импульсов 1, контура 2 и осциллографа 3. Генератор импульсов формирует импульсы напряжения, которые поступают на конденсатор С контура. При разряде конденсатора в контуре возникают свободные затухающие колебания. Регистрируется этот колебательный процесс с помощью осциллографа: на его экране получим картину затухающих колебаний, показанную на рис.2.
Длительность импульсов t генератора 1 много меньше периода Тг их повторения, так что в интервале (Тг - t) колебания между импульсами в контуре успевают затухать до поступления на конденсатор следующего импульса. В работе требуется измерить период свободных колебаний контура Т, определить логарифмический декремент затухания l, критическое сопротивление контура Rкрит. И добротность контура Q. Логарифмический декремент затухания l можно определить непосредственно по осциллограмме затухающих колебаний (рис.2), используя формулу (10). Если увеличивать активное сопротивление контура R, изменяя сопротивление магазина сопротивлений, то при R = Rкрит. на экране осциллографа получится картина апериодической разрядки конденсатора (рис.3, кривая а). При определении Rкрит. нужно учесть, что активное сопротивление контура
где RL - активное сопротивление катушки индуктивности; Rг - сопротивление генератора импульсов; Rмаг. - переменное сопротивление резистора (магазина).
Задание 1. Ознакомиться с инструкцией по работе с осциллографом. 2. Рассчитать период затухающих колебаний контура для трех значений емкости С по приближенной форме 3. Получить на экране осциллографа картину свободных затухающих колебаний контура. Определить период колебаний Т для трех значений емкости С при нулевом сопротивлении магазина. Измеренные значения периода нанести на теоретический график зависимости Т от 4. Для контура с одним из значений емкости измерить логарифмический декремент при различных сопротивлениях магазина, введенных в контур. 5. В координатах l, R построить график зависимости логарифмического декремента затухания от сопротивления контура. Определить по графику суммарное сопротивление генератора импульсов и катушки индуктивности (RL + Rг). 6. Измерить сопротивление магазина Rмаг. При критическом сопротивлении контура. Найти Rкрит., учитывая согласно (15) также и значения (RL + Rг), определенные в п.5. 7. Рассчитать Rкрит. по формуле (13). 8. Оценить добротность контура Q по формуле (14) при разных сопротивлениях контура.
Контрольные вопросы
1. Какие колебания называются свободными ? 2. Как получить уравнение затухающих электромагнитных колебаний ? Какой вид имеет его решение ? 3. Что такое период свободных затухающих колебаний ? От чего он зависит ? 4. Что понимают под амплитудой затухающих колебаний ? 5. Чем определяется частота затухающих колебаний ? 6. Какие характеристики служат количественной мерой затухания ? Как они связаны с параметрами контура и между собой ? 7. Как измерить логарифмический декремент затухания ? От каких параметров контура он зависит ? 8. Как измерить и рассчитать критическое сопротивление контура ? 9. Каково назначение генератора импульсов в цепи контура ? 10.При каком условии допустимо применять формулу Томсона для расчета периода затухающих колебаний ?
|




 (2)
(2) (3)
(3) , (4)
, (4)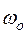 — собственная частота контура, т.е. частота свободных незатухающих колебаний без потерь энергии (при R = 0), уравнение (2) можно преобразовать следующим образом:
— собственная частота контура, т.е. частота свободных незатухающих колебаний без потерь энергии (при R = 0), уравнение (2) можно преобразовать следующим образом: . (5)
. (5)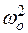 , решение уравнения (5) имеет вид
, решение уравнения (5) имеет вид , (6)
, (6) (7).— частота затухающих колебаний в контуре.
(7).— частота затухающих колебаний в контуре.
 постепенно уменьшается по закону
постепенно уменьшается по закону  (рис.2).
(рис.2). . (8)
. (8)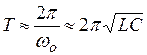 (Формула Томсона). (9)
(Формула Томсона). (9)

 .
. (10)
(10) (рис.2) понимают амплитуды либо заряда, либо тока, либо напряжения в моменты времени t и (t + T). Заменив в (10) d и Т в соответствии с (3) и (8), имеем
(рис.2) понимают амплитуды либо заряда, либо тока, либо напряжения в моменты времени t и (t + T). Заменив в (10) d и Т в соответствии с (3) и (8), имеем . (11)
. (11) и
и (12)
(12)
 :
:


 . В координатах Т и
. В координатах Т и  построить график зависимости периода колебаний от емкости по вычисленным значениям Т.
построить график зависимости периода колебаний от емкости по вычисленным значениям Т.