 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задачи для самостоятельного решения
Механические и электромагнитные колебания
Методические указания и задания для студентов – бакалавров по направлению 151900 «Конструкторско – технологическое обеспечение машиностроительного производства» Контрольная работа №5
Вологда Требования к оформлению и общие методические указания по выполнению индивидуальных домашних заданий 1. Студентам, изучающим курс физики в течение двух семестров, необходимо решить в течение семестра 6 задач по первой части пособия. 2. Номер варианта совпадает с порядковым номером студента в журнале. 3. Номера задач в зависимости от номера варианта определяются по формуле: Nзадачи =30n+ Nварианта, где n=0, 1, ...9 или по таблице вариантов. 4. Задания должны выполняться последовательно по пройденным темам. Сроки представления решенных задач объявляются преподавателем. 5. Задачи оформляются в письменном виде на отдельных листах. Решение каждой задачи необходимо начинать с новой страницы. 6. Требуется указать номер варианта и номер задачи по нумерации пособия. 7. Условие задачи переписывается полностью, без сокращений. 8. Решение записывается в стандартном виде:
:
Ответ:
9. Все физические величины необходимо выразить в системе единиц СИ. 10.Сделать рисунок, схему, если это необходимо. 11.Сформулировать основные законы, записать формулы, на которых базируется решение. Обосновать возможность их применения в условиях данной задачи. Составить полную систему уравнений для решения задачи. 12.Получить окончательное выражение искомой величины в общем виде. Проверить размерность. 13.Подставить числовые данные и рассчитать искомую величину. 14. Проанализировать полученный результат. 15.Записать ответ. 16.Каждую задачу требуется защитить, то есть полностью объяснить решение задачи преподавателю.
Таблица вариантов
Примеры решения задач Задача 1
Точка участвует одновременно в двух колебаниях одного направления: х1 = А соs ωt и х2 = А соs 2 ωt . Найти максимальную скорость точки.
Решение:
Скорость можно определить, как первую производную от смещения
Значение скорости меняется со временем по закону
Чтобы найти
Можно представить cos 2ωt = cos2 ωt – sin2 ωt = 2 cos2 ωt – 1 Тогда для нахождения функции скорости необходимо решить следующее уравнение:
или 8 ω2А cos2 ωt + ω2Acos ωt – 4 ω2А = 0. Получилось квадратное уравнение относительно соs ωt . Решением этого уравнения является значение косинуса: соs ωt1 = 0,648 и соs ωt2 = -0,773.
Им соответствует: sinωt1 = 0,76; sin 2ωt1 = - 0,99; sinωt 2 = 0,63; sin 2ωt 2 = -0,98. Тогда, подставляя соответствующие значения в выражение для скорости
Максимальное значение скорости по модулю будет 2,74 ωA, то есть больше той скорости, что имела бы точка, участвуя в каждом из колебаний в отдельности.
Задача 2
Задача 3 В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами и одинаковыми периодами получается результирующее колебания с тем же периодом и той же амплитудой. Найти разность фаз складываемых колебаний.
Задача 4
Задача 5
Задача 6
Задача 7
Задача 8
Задача 9
Задача 10
Задача 11
Задача 12
Задача 13
Задача 14
Задача 15
Задача 16
Задача 17
Задача 18
Задача 19
Задача 20
Задача 21
Задача 22
Задачи для самостоятельного решения Задача1. Математический маятник совершает гармонические колебания по закону х=1,5соs(4/3 ду колебаний, начальную фазу, период колебаний, частоту. Построить график колебаний.
Задача 2.Упругий шарик падает на гладкую стальную поверхность с высоты 1 м. Какие колебания будет совершать шарик, если удар о стальную поверхность считать абсолютно упругим? Нарисуйте примерный график колебаний. Определите период колебаний маятника.
Задача 3.Упругий шарик падает на гладкую стальную поверхность с высоты 1 м. Какие колебания будет совершать шарик, если удар о стальную поверхность считать абсолютно упругим? Определите длину математического маятника.
Задача 4.Грузик пружинного маятника массой 10 г сместили от положения равновесия на 2 см. При этом сила, действующая на грузик, оказалась равной 0,5 Н. После измерения силы грузик отпустили. Полагая, что грузик маятника совершает гармонические колебания, напишите уравнение колебаний и постройте векторную диаграмму.
Задача 5.Упругий шарик падает на гладкую стальную поверхность с высоты 1 м. Какие колебания будет совершать шарик, если удар о стальную поверхность считать аболютно упругим? Определите максимальное значение скорости и ускорения грузика математического маятника.
Задача 6.Напишите уравнения колебаний напряжения в сети переменного тока (U= 220 В, v = 50 Гц).
Задача 7.В сеть переменного тока (U = 220 В, v = 50 Гц) включены: а) катушка с индуктивностью 1 Гн; б) конденсатор емкостью 5 мкФ. Напишите уравнение токов в цепи с катушкой и конденсатором. Постройте векторные диаграммы колебаний.
Задача 8.Точка совершает гармонические колебания с периодом 0,5 с. В момент прохождения положения равновесия скорость точки равна 10 см/с. Написать уравнение колебаний точки.
Задача 9.Математический маятник, имеющий длину 1 м и массу грузика 25 г, совершает гармонические колебания. Определите полную энергию колебания, если амплитуда равна 3 см.
Задача 10. В момент времени t = 0 конденсатор колебательного контура емкостью 8 нФ имеет заряд 1,б*10-7 Кл. Индуктивность контура 2 мГн. Определить напряжение на конденсаторе в момент времени t = 3 мкс.
Задача 11.Найти разность фаз двух гармонических колебаний, заданных уравнениями:
X1= 2 sin(3t + x2 = 4sin(3t + 3/4 Задача 12.Написать уравнение движения, получающего в результате сложения двух одинаково направленных гармонических колебательных движений с одинаковым периодом 8 с и одинаковой амплитудой 0,02 м. Разность фаз между этими колебаниями равна Начальная фаза одного из этих колебаний равна нулю.
Задача 13.Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленных колебаний, данных уравнениями Х1 = 0,02 sin(5
Задача 14.I) Найти амплитуду и начальную фазу гармонического колебания, полученного от сложения одинаково направленныхsin колебаний, данных уравнениями х1 = 4sin 2) Написать уравнение результирующего колебания. 3) Дать векторную диаграмму сложения амплитуд.
Задача 15.Даны два гармонический колебания х1= 3 sin4 Построить график этих колебаний. Сложить графически эти колебания. Построить график результирующего колебания.
Задача 16.Написать уравнение результирующего колебания, получающегося в результате сложения двух одинаково направленных колебаний с одинаковой частотой v1= v2 = 5Гц. и с одинаковой начальной фазой ф1 = ф2 = 60°. Амплитуда одного из колебаний равна а1 = 0,1 м, амплитуда другого А2 = 0,05 м.
Задача 17.Точка участвует в двух колебаниях одинакового периода с одинаковыми начальными фазами. Амплитуда колебаний а1 = 3 см и А2 = 4 см. Найти амплитуду результирующего колебания, если: 1) колебания совершаются в одном направлении; 2) колебания взаимно перпендикулярны.
Задача 18.Точка участвует одновременно в двух взаимно перпендикулярных колебаниях х = 2 sin ωt и у = 2 соs ωt. Найти траекторию движения точки.
Задача 19.Точка участвует одновременно в двух взаимно перпендикулярных колебаниях х = sin
Задача 20. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях х = соs
Задача 21. Складываются два гармонических колебания одного направления с одинаковыми периодами 1,5 с и амплитудами 2см, начальные фазы колебаний ф1 = и начальную фазу результирующего колебания. Написать его уравнение. Построить с соблюдением масштаба векторную диаграмму сложения амплитуд.
Задача 22.Два гармонических колебания, одинаково направленных и одинакового периода, складываются в одно колебание с амплитудой 4 см. Разность фаз складываемых колебаний равна 60°,амплитуда первого колебания 2 см, определить амплитуду второго колебания; дать векторную диаграмму сложения амплитуд.
Задача 23. Складываются два колебания, совпадающие по направлению и выражаемые уравнениями: X, = соs Определить амплитуду и начальную фазу результирующего колебания, написать его уравнение и дать векторную диаграмму сложения амплитуд.
Задача 24.Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями: х = 3 соs Определить траекторию точки и начертить ее с соблюдением масштаба.
Задача 25. То же, если колебания выражаются уравнениями: Х = соs Задача 26.Материальная точка участвует в двух колебаниях, происходящих по одной прямой и выражаемых уравнениями: X1 = sin t х2 = 2 cost. Найти амплитуду сложного движения, его частоту и начальную фазу; написать уравнение движения.
Задача 27. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям и выражаемых уравнениями:
X = sin t/2 , У = cost. Найти уравнение траектории точки и начертить траекторию с соблюдением масштаба.
Задача 28.При сложении двух одинаково направленных гармонических колебаний с одной и той же частотой и амплитудами, равными 2 и 4 см, получается гармоническое колебание с амплитудой 5 см, найти разность фаз складываемых колебаний.
Задача 29.Материальная точка одновременно участвует в двух взаимно перпендикулярных колебаниях, описываемых уравнениями
Х = 2 cos
Задача 30.На вертикально и горизонтально отклоняющиеся пластины осциллографа поданы напряжения Uу = а sinωt и Uх = b соs 2 ωt . Определить траекторию луча на экране осциллографа.
Задача 31.Точка участвует в двух взаимно-перпендикулярных колебаниях: X = А1 *соs ω1t, X = А2 *соs ω2t где А, = 4 см, ω1 = 1 с -1; А2 = 6 см. ω1 = ω1 /2 Найти траекторию движения точки.
Задача 32.Даны два гармонических колебания х1= 3 sin4
Задача 33. В результате сложения двух одинаково направленных гармонических колебаний с одинаковыми амплитудами и одинаковыми периодами получается результирующее колебание с тем же периодом и той же амплитудой. Найти разность фаз складываемых колебаний.
Задача 34. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях х= cos
Задача 35.Логарифмический декремент затухания математического маятника равен 0,2. Найти, во сколько раз уменьшится амплитуда колебаний за одно полное колебание маятника.
Задача 36. Чему равен логарифмический декремент затухания математического маятника, если за 1 мин амплитуда колебаний уменьшилась в два раза? Длина маятника 1 м. ' Задача 37.Математический маятник длиной в 24,7 см совершает затухающие колебания. Через сколько времени энергия колебаний маятника уменьшится в 9,4 раза? Задачу решить при значении логарифмического декремента затухания: 1)0,01 и 2) 1.
Задача 38.Амплитуда затухающих колебаний математического маятника за 1 мин уменьшилась вдвое. Во сколько раз она уменьшится за 3 мин? Задача 39.Математический маятник длиной 0,5 м, выведенный из положения равновесия, отклонился при первом колебании на 5 см, а при втором (в ту же сторону) - на 4 см. Найти время релаксации, то есть время, в течение которого амплитуда колебаний уменьшится в е раз, где е - основание натуральных логарифмов.
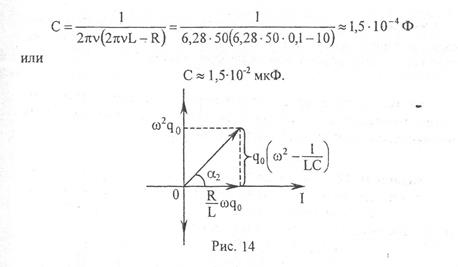
Задача 40.Колебательный контур состоит из конденсатора емкостью 0,2 мкФ и катушки индуктивностью 5,07*10-3 Г. 1) При каком логарифмическом декременте затухания разность потенциалов на обкладках конденсатора за 10 -3 с. уменьшится в три раза? 2) Чему при этом равно сопротивление контура?
Задача 41. Колебательный контур состоит из индуктивности в 10 -3Г, емкости в 0,405 мкФ и сопротивления в 2 Ом. Найти, во сколько раз уменьшится разность потенциалов на обкладках конденсатора за время одного периода.
Задача 42. Колебательный контур состоит из конденсатора емкостью 2,22*10 -9 Ф и катушки, намотанной из медной проволоки диаметром 0,5 мм. Длина катушки 20 см. Найти логарифмический декремент затухания колебаний.
Задача 43.Колебательный контур имеет емкость 1,1-10 -9Ф и индуктивность 5-10 -3 Г. Логарифмический декремент затухания равен 0,005. За сколько времени потеряется вследствие затухания 99 % энергии контура?
Задача 44. Математический маятник длиной 1,2 м колеблется в среде с малым сопротивлением. Считая, что сопротивление среды не влияет на период колебания маятника, найти коэффициент затухания и логарифмический декремент затухания, если за 8 мин амплитуда колебаний маятника уменьшилась в три раза.
Задача 45.Начальная амплитуда колебаний механического маятника А1= 20 см, амплитуда после 10 полных колебаний равна а10 = 1 см. Определить логарифмический декремент затухания и коэффициент затухания, если период колебаний Т = 5 с записать уравнение колебания.
Задача 46. Амплитуда затухающих колебаний маятника за время 5 мин уменьшилась в два раза. За какое время, считая от начального момента, амплитуда уменьшится в восемь раз?
Задача 47. За время 8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания.
Задача 48.Амплитуда колебаний маятника длиной 1 м за время 10 мин уменьшилась в два раза. Определить логарифмический декремент затухания.
Задача 49.Логарифмический декремент затухания колебаний маятника 0,003. сколько полных колебаний должен сделать маятник, чтобы амплитуда уменьшилась в 2 раза?
Задача 50.Тело массой 5 г совершает затухающие колебания. В течение времени 50 с тело потеряло 60 % своей энергии. Определить коэффициент сопротивления.
Задача 51. Амплитуда затухающего колебания уменьшается за 1 период в 2 раза. Определить логарифмический декремент затухания.
Задача 52.Колебательный контур состоит из конденсатора ёмкостью 0,02 мкФ, катушки с индуктивностью 4,5 мГн и сопротивления 5 Ом. Найти, во сколько раз уменьшится разность потенциалов на обкладках конденсатора за время одного периода? За время двух периодов? Определить добротность колебательного контура. Задача 53.Для определения добротности колебательного контура на экране осциллографа наблюдаются затухающие колебания. При этом установлено, что амплитуда десятого колебания в 2 раза меньше первого. Рассчитайте добротность колебательного контура.
Задача 54. На тело с массой 10 г, совершающее затухающие колебания, начала действовать внешняя периодическая сила, под действием которой установились вынужденные колебания. Уравнения вынужденных колебаний имеют вид: х = 5 соs(10
Задача 55.Резонансная характеристика колебательного контура представляет собой зависимость амплитуды напряжения (или тока) от частоты вынуждающей силы. Нарисовать (качественно) резонансные характеристики колебательного контура, если его добротность равна: а) 10; б) 100; в) 1000; г) ∞ ?
Задача 56. К последовательному колебательному контуру, состоящему из конденсатора емкостью 0,05 мкФ, катушки с индуктивностью 1,2 мГн и сопротивления 1,2 Ом, подано напряжение, -изменяющееся по закону U = 2,5 соs ωt. Определите напряжение на конденсаторе контура при резонансе. Нарисуйте электрическую схему включения контура. Задача 57. Колебательный контур состоит из катушки с индуктивностью 0,06 мГн и сопротивлением 2 Ом, и конденсатора емкостью 0,04 мкФ. Какую мощность потребляет контур при резонансе, если в нем поддерживаются незатухающие колебания с амплитудой 1,5В?
Задача 58.На вход радиоприемника поступает последовательность прямоугольных импульсов с периодом 5 мкс. При перестройке приемника наблюдается несколько резонансных частот. Определите эти частоты.
Задача 59.Цепь, состоящую из последовательно соединенных конденсатора емкости С и сопротивления R, подключили к переменному напряжению U= Um соs ωt в момент t = 0. Найти ток в цепи как функцию времени t.
Задача 60.Концы цепи, состоящей из последовательно включенных конденсатора и активного сопротивления R = 110 Ом, подсоединили к переменному напряжению с амплитудой Um = 110 В. При этом амплитуда установившегося тока в цепи Im = 0,50 А. Найти разность фаз между током и подаваемым напряжением.
Задача 61. Цепь из последовательно соединенных конденсатора емкости С = 22 мкФ и катушки с активным сопротивлением R= 20 Ом и индуктивностью L = 0,35 Гн подключена к сети переменного напряжения с амплитудой Um = 180 В и частотой ω = 314 с-1 . Найти: а) амплитуду тока в цепи; б) разность фаз между током и внешним напряжением; в) амплитуды напряжения на конденсаторе и катушке.
Задача62.В контуре, добротность которого (Q = 50 и собственная, частота колебаний Vо =5,5 кГц, возбуждаются затухающие колебания. Через сколько времени энергия, запасенная в контуре, уменьшится в ῃ = 2,0 раза?
Задача 63.На сколько процентов отличается частота со свободных колебаний контура с добротностью Q = 5,0 от собственной частоты ωо колебаний этого контура?
Задача 64.Переменное напряжение с частотой ω = 314 с и амплитудой Um = 180 В подключено к концам цепи, состоящей из последовательно соединенных конденсатора и катушки с активным сопротивлением R = 40 Ом и индуктивностью L = 0,36 Гн. При каком значении емкости конденсатора амплитуда напряжения на катушке будет максимальной? Чему равна эта амплитуда и соответствующая амплитуда напряжения на конденсаторе?
Задача 65.Последовательно соединенные конденсатор емкости С = 45 мкФ и катушка с активным сопротивлением подключены к источнику гармонического напряжения, частоту которого можно менять, не изменяя его амплитуды. При частотах v1 - 1,50 кГн и V2 = 2,50 кГц амплитуда тока оказалась одинаковой. Найти индуктивность катушки.
Задача 66. Точка совершает колебания с частотой ω = 25 с-1. Найти коэффициент затухания β, если в начальный момент скорость точки равна нулю, а ее смещение из положения равновесия в ῃ = 1,020 раза меньше амплитуды.
Задача 67. К пружине подвесили грузик, и она растянулась на ∆r = 9,8 см с каким периодом будет колебаться грузик в вертикальном направлении? Логарифмический декремент затухания λ = З,1. Задача 68. Магнитная антенна приемника диапазона длинных волн представляет собой цилиндрическую катушку, намотанную на ферритовом стержне по всей его длине. Ферритовый стержень имеет длину 20 см, диаметр 1 см, магнитную проницаемость µ =•1500. Определить число витков катушки, если для настройки на частоту 150 кГц необходим конденсатор емкостью 500 пФ. При расчете полагать катушку антенны бесконечно длинным соленоидом.
Задача 69. Детекторный приемник должен работать в диапазоне частот от 150 кГц до 450 кГц. Для перестройки колебательного контура используется конденсатор переменной емкости, емкость которого изменяется от 12 пФ до 450 пФ. Рассчитайте элементы колебательного контура, если емкость Со монтажа, катушки и детектора (диода) равна 20 пФ. Задача 70. Свободные колебания в контуре без потерь имеют амплитуду напряжения 50 В, амплитуду тока 40 мА и частоту 2 МГц. Определить параметры контура.
Задача 71. Колебательный контур состоит из конденсатора емкостью 0,05 мкФ и катушки с индуктивностью 0,05 Гн. Амплитуда напряжения в контуре 90 В. Получите уравнение зависимости энергии электрического и магнитного поля от времени.
Задача 72. Материальная точка совершает гармонические колебания вдоль оси X. По прошествии времени t1= 0,1 с от начала движения смещение точки от положения равновесия X1 = 5 см, скорость υ1х = 62 см/с, ускорение α1х = - 540 см/с² Определить: 1) амплитуду, циклическую частоту и начальную фазу колебаний; 2) смещение, скорость и ускорение в начальный момент (t = 0).
Задача 73. Материальная точка совершает гармонические колебания вдоль оси ОХ с периодом Т и амплитудой Х0. За какое время, считая от начала движения, она пройдет расстояние s = Хо/2; Х0 (см. рис. а и б). Начальная фаза α0 - 0; π/2.
Задача 74. Материальная точка массой m = 5 г совершает гармонические колебания с частотой V = 0,5 1/с. Амплитуда колебаний А = 3 см. Определить: 1) скорость о точки в момент времени, когда смещение х = 1,5 см; 2) максимальную силу Рmах, действующую на точку; 3) полную энергию Е колеблющейся точки.
Задача 75. Точка равномерно обращается по окружности против часовой стрелки с периодом Т = 12 с. Диаметр окружности d = 20 см. Написать уравнение движения проекции точки "на прямую, касательную к окружности. За начало отсчета времени принять момент, когда точка, обращающаяся по окружности, проходит через точку касания. Задача 76. Каковы значения смещения х, скорости υ и ускорения α колеблющейся точки из предыдущей задачи в конце первой секунды после начала колебаний?
Задача 77. Точка совершает гармонические колебания с амплитудой А = 10 см и периодом Т = 2 с. Написать уравнение этих колебании. Определить также фазу φ для двух моментов времени: 1) когда смещение точки х = 6 см; 2) когда скорость точки υ = 10 см/с
Задача 78. Уравнение колебаний точки имеет вид х = 0,08соsπ (1 + 0,2). Определить амплитуду, период и начальную фазу колебаний. Задача 79. Найти амплитуду А, период Т, частоту V и начальную фазу ф колебания, заданного уравнением х= 5 sin (39,2t + 5,2) / 5 (длина в сантиметрах, время в секундах). Задача 80. Уравнение колебаний точки имеет вид х = 2sin 5t (длина в сантиметрах, время в секундах). Определить максимальные значения скорости υ и ускорения α точки.
Задача 81. Точка колеблется гармонически. Амплитуда колебаний А = 5 см, круговая частота ω = 2 * 1/с, начальная фаза φ = 0. Определить ускорение точки в момент, когда ее скорость V = 8см/с. Задача 82. Точка совершает гармонические колебания по закону синуса. Наибольшее смещение точки А = 10 см, наибольшая, скорость V = 20 см/с. Написать уравнение колебаний и найти максимальное значение а точки.
Задача 83. Точка совершает гармонические колебания. Максимальная скорость точки υ max=10 см/с, максимальное ускорение α max = 100 см/ с² . Найти циклическую частоту со колебаний, их период Т и амплитуду А. Написать уравнение колебаний. Задача 84. Точка совершает гармонические колебания. В некоторый момент времени t смещение точки X1 = 5 см. При увеличении фазы вдвое смещение точки стало х2 = 8 см. Найти амплитуду А колебаний. Задача 85 Точка совершает гармонические колебания. В некоторый момент времени t смещение точки х = 5 см, ее скорость υ = 20 см/с и ускорение а = 80 см/ с² . Найти: амплитуду А, циклическую частоту со, период колебаний Т и фазу ф колебаний в рассматриваемый момент времени.
Задача 86. Написать уравнение гармонического колебательного движения с амплитудой в 0,1 м, периодом 4 с и начальной фазой колебаний, равной 45°. Начертить график этого движения.
Задача 87. Написать уравнение гармонического колебательного движения с амплитудой в 0,1 м, периодом 4 с и начальной фазой, равной нулю.
Задача 88. Амплитуда гармонических колебаний равна 50 мм, период 4 с и начальная фаза π/4. 1) Написать уравнение этого колебания. 5) Найти смещение колеблющейся точки от положения равновесия при t = 0 и t = 1,5 с; 3) Начертить график этого движения.
Задача 89. Написать уравнение гармонического колебательного движения, если начальная фаза колебаний равна: 1) 0; 2) π/2 ; 3) π; 4)3/2 π; 5) 2 π .Амплитуда колебаний 5 см и период колебаний 8 с. Начертить график колебаний во всех этих случаях. Задача 90. Через сколько времени от начала движения точка, совершающая гармоническое колебание, сместится от положения равновесия наполовину амплитуды? Период колебаний равен 24 с, начальная фаза равна нулю.
Задача 91. Начальная фаза гармонического колебания равна нулю. Через какую долю периода скорость точки будет равна половине ее максимальной скорости? Задача 92. Через сколько времени от начала движения точка, совершающая колебательное движение по уравнению х = 7sin 0,5πt, проходит путь от положения равновесия до максимального смещения? Задача 93. Амплитуда гармонического колебания равна 5 см, период 4 с. Найти максимальную скорость колеблющейся точки и ее максимальное, ускорение.
Задача 94. Уравнение движения точки дано в виде х = 2sin( π/2*t + π/4) см. Найти: 1) период колебаний;2) максимальную скорость точки; 3) ее максимальное ускорение. Задача 95. Уравнение движения точки дано в виде х = sin π/6 * t Найти моменты времени, в которые достигаются максимальная скорость и максимальное ускорение. Задача 96. Точка совершает гармоническое колебание. Период колебаний 2 с, амплитуда 50 мм, начальная фаза равна нулю. Найти скорость точки в момент времени, когда смещение точки от положения равновесия равно 25 мм. Задача 97. Написать уравнение гармонического колебательного движения, если максимальное ускорение точки 49,3 см/ с² , период колебаний 2 с и смещение точки от положения равновесия в начальный момент времени 25 мм.
Задача 98. Начальная фаза гармонического колебания равна нулю. При смещении точки от положения равновесия, равном 2,4 см, скорость точки равна 3 см/с, а при смещении, равном 2,8 см, скорость равна 2 см/с. Найти амплитуду и период этого колебания.
Задача 99. Уравнение колебаний материальной точки массой 1,6 * 10-2 кг имеет вид х = 0,1 sin ( π/8 * t + π/4), м . Построить график зависимости от времени (в пределах одного периода) силы Р, действующей на точку. Найти значение максимальной силы. Задача 100. Материальная точка массой 10 г колеблется по уравнению х = sin (π/5 * t + π/4) , см. Найти максимальную силу, действующую на точку, и полную энергию колеблющейся точки.
Задача 101. Уравнение колебания материальной точки массой в 16 г имеет вид х = 2 sin (π/4 * t + π/4) , см. Построить график зависимости от времени (в пределах одного периода) кинетической, потенциальной и полной энергий точки. Задача 102. Чему равно отношение кинетической энергии точки, совершающей гармоническое колебание, к её потенциальной энергии для моментов времени: 1) t = T/12, с; 2) t = T/8, с: 3) t = T/6, с. Начальная фаза колебаний равна нулю. Задача 103. Чему равно отношение кинетической энергии точки, совершающей гармоническое колебание, ее потенциальной энергии для моментов, когда смещение точки от положения равновесия составляет: 1) х = А/4; 2) х = А/2; 3) х = А, где А-амплитуда колебаний . Задача 104. Полная энергия тела, совершающего гармоническое колебательное движение, равна 3 • 5 * 10-5 Дж, максимальная сила, действующая на тело, равна 1,5 * 10-3 Н. Написать уравнение движения этого тела, если период колебаний равен 2 с и начальная фаза 60°.
Задача 105. Амплитуда гармонических колебаний материальной точки А = 2 см, полная энергия колебаний 3 * 10-7Дж. При каком смещении от положения равновесия на колеблющуюся точку действует сила 2,25 * 10-5 Н?
Задача 106. К пружине подвешен груз 10 кг. Зная, что пружина под влиянием силы в 9,8 Н растягивается на 1,5 см, определить период вертикальных колебаний груза. Задача 107. Колебательный контур состоит из конденсатора емкостью 8 8 * 10-10 Ф и катушки, индуктивность которой равна 2 * 10-3 На какую длину волны настроен контур? Сопротивлением контура пренебречь. Задача 108. На какой диапазон волн можно настроить колебательный контур, если его индуктивность равна 2 * 10-3 Г, а емкость может меняться от 6,9 * 10-11 Ф до 53,4 * 10-11 Ф? Сопротивление кон-тура ничтожно мало. Задача 109. Какую индуктивность надо включить в колебательный контур, чтобы при емкости в 2 мкФ получить звуковую частоту 1000 Гц? Сопротивлением контура пренебречь.
Задача 110. Катушка, индуктивность которой 3 * 10-5 Г, присоединена к. плоскому конденсатору с площадью пластин 100 см² и_расстоянием между ними 0,1 мм. Чему равна диэлектрическая проницаемость среды, заполняющей пространство между пластинами, если контур резонирует на волну длиной 750 м?
Задача 111. Колебательный контур состоит из конденсатора емкостью 0,025 мкФ и катушки с индуктивностью 1,015 Г. Омическим сопротивлением цепи пренебрегаем. Конденсатор заряжен количеством электричества 2,5*10-6 Кл. 1) Написать для данного контура уравнение (с числовыми коэффициентами) изменения разности потенциалов на обкладках конденсатора и силы тока в цепи в зависимости от времени. 2) Найти значения разности потенциалов на обкладках конденсатора и силы тока в цепи в моменты времени Т/8, Т/ 4, Т/2 3) Построить графики этих зависимостей в пределах одного периода. Задача 112. Для колебательного контура предыдущей задачи: 1) Написать уравнение (с числовыми коэффициентами) изменения со временем энергии электрического поля, энергии магнитного поля и полной энергии. 2) Найти значение энергии электрического поля, энергии магнитного поля и полной энергии в моменты времени Т/8, Т/4 и Т/2. 3) Построить графики этих зависимостей в пределах одного периода.
|



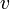 -?
-?  ' = - ω2Acos ωt- 4 ω2A cos 2ωt.
' = - ω2Acos ωt- 4 ω2A cos 2ωt.






















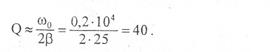









 t +
t +