 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| основы молекулярно-кинетической теории
Молекулярно-кинетическая теория - теория, объясняющая тепловые явления в макроскопических телах и свойства этих тел на основе их молекулярного строения. Основные положения молекулярно-кинетической теории: 1. вещество состоит из частиц - молекул и атомов, разделенных промежутками, 2. эти частицы хаотически движутся, 3. частицы взаимодействуют друг с другом. В МФ рассматриваются: - строение вещества; - его изменение под влиянием внешних факторов (давления, температуры, электромагнитного поля); - явления переноса (диффузия, теплопроводность, вязкость); - фазовое равновесие и процессы фазовых переходов (кристаллизация, плавление, испарение, конденсация); - критическое состояние вещества; - поверхностные явления на границах раздела фаз.
2. Статистическое описание поведения молекул. К концу XIX в. была создана последовательная теория поведения больших общностей атомов и молекул – молекулярно-кинетическая теория, или статистическая механика. Многочисленными опытами была доказана справедливость этой теории. Процессы, изучаемые молекулярной физикой, являются результатом совокупного действия огромного числа молекул. Поведение громадного числа молекул анализируется с помощью статистического метода. Он основан на том, что свойства макроскопической системы в конечном результате определяются свойствами частиц системы, особенностями их движения и усредненными значениями кинетических и динамических характеристик таких частиц (скорости, энергии, давления и т. д.). Например, температура тела определяется скоростью беспорядочного движения его молекул, но так как в любой момент времени разные молекулы имеют различные скорости, она может быть выражена только через среднее значение скорости движения молекул. Нельзя говорить о температуре одной молекулы. Макроскопические характеристики тел имеют физический смысл лишь в случае большого числа молекул. Статистические же методы позволяют на основе данных о строении вещества определить такие параметры. Однако количественная теория твердого и особенно жидкого состояния вещества очень сложна, поэтому в ряде случаев простые расчеты, основанные на законах термодинамики, оказываются незаменимыми. В настоящее время в науке и технике широко используются как термодинамические, так и статистические методы описания свойств микросистемы.
3. Силы взаимодействия между атомами и молекулами. Если бы между молекулами не существовало сил притяжения, то все тела при любых условиях находились бы только газообразном состоянии. Но одни силы притяжения не могут обеспечить существования устойчивых образований из атомов и молекул. На очень малых расстояниях между молекулами обязательно действуют силы отталкивания. Благодаря этому молекулы не проникают друг в друга и куски вещества никогда не сжимаются до размеров одной молекулы. Молекула - это сложная система, состоящая из отдельных заряженных частиц: электронов и атомных ядер. Хотя в целом молекулы электрически нейтральны, тем не менее между ними на малых расстояниях действуют значительные электрические силы: происходит взаимодействие электронов и атомных ядер соседних молекул. Если молекулы находятся на расстояниях, превышающих их размеры в несколько раз, то силы взаимодействия практически не сказываются. Силы между электрически нейтральными молекулами являются короткодействующими. На расстояниях, превышающих 2 - 3 диаметра молекул, действуют силы притяжения. По мере уменьшения расстояния между молекулами сила притяжения сначала увеличивается, а затем начинает убывать и убывает до нуля, когда расстояние между двумя молекулами становится равным сумме радиусов молекул. При дальнейшем уменьшении расстояния электронные оболочки атомов начинают перекрываться, и между молекулами возникают быстро нарастающие силы отталкивания. 4. Равновесные и неравновесные состояния системы. Термодинамически равновесное состояние тела или системы это такое состояние теплового и механического равновесия элементов тела или системы, которое без внешнего воздействия может сохраняться сколь угодно долго. Равновесная система это система тел, находящихся в термодинамическом равновесии, в противном случае она будет называться неравновесной системой. Так, без учета гравитационных сил, равновесное состояние тела или системы есть такое их состояние, при котором по всему их объему давления и температуры имеют одинаковые значения. Равенство только давления во всех точках обусловливает механическое равновесие, равенство температур - термическое равновесие. При неравновесном состоянии тела (системы) в разных его частях могут быть различны и температуры и давления. Однако в неравновесной системе могут быть точки, в которых некоторые термические параметры одинаковы. Геометрическое место точек в пространсве, занимаемом системой (телом), с одинаковыми температурами представляет собой изотермическую поверхность, а с одинаковым давлением - изобарическую поверхность. Такие поверхности называются изопотенциальными. Изопотенциальные поверхности не могут пересекаться. Изопотенциальные поверхности могут быть и при равновесном состоянии тела. Например, в высоком цилиндре с жидкостью на различных уровнях от его дна будут различные изобарные поверхности, обусловленные действием гравитационного поля земли. Поэтому равенство параметров в равновесной системе делается с оговоркой - без учета гравитационных сил.
5. Внутренняя энергия системы. Внутренняя энергия - это энергия системы за вычетом ее полной механической энергии (которая складывается из кинетической энергии системы как целого и ее потенциальной энергии в поле внешних сил): Для идеального газа внутренняя энергия равна суммарной кинетической энергии хаотическогодвижения всех N молекул газа: Внутренняя энергия системы аддитивна, т.е. складывается из внутренних энергий ее частей. Внутренняя энергия системы является функцией состояния. Поэтому приращение внутренней энергии (как и приращение всех функций состояния) всегда будет полным дифференциалом dU. При циклическом процессе, когда система приходит в исходное состояние, ее внутренняя энергия не меняется. 6. Идеальный газ. Уравнения его состояния. Идеальный газ — математическая модель газа, в которой в рамках молекулярно-кинетической теории предполагается, что: 1) потенциальной энергиейвзаимодействия частиц, составляющих газ, можно пренебречь по сравнению с ихкинетической энергией; 2) суммарный объём частиц газа пренебрежимо мал; 3) между частицами нет дальнодействующих сил притяжения или отталкивания, соударения частиц между собой и со стенками сосуда абсолютно упруги; 4) время взаимодействия между частицами пренебрежимо мало по сравнению со средним временем между столкновениями. Пусть газ массой m занимает объем V при температуре Т и давлении р, а М- молярная масса газа. По определению, концентрация молекул газа: n = N/V, где N-число молекул. Подставим это выражение в основное уравнение молекулярно-кинетической теории: Величину R называют универсальной газовой постоянной, а уравнение, записанное в виде называют уравнением состояния идеального газа или уравнением Менделеева-Клапейрона. Нормальные условия - давление газа равно атмосферному (р = 101,325 кПа) при температуре таяния льда (Т = 273,15 К ).
7. Газовые законы. Изопроцессы. Изотермическим процессом называются изменения состояния газа, протекающие при постоянной температуре.
Для газа данной массы произведение давления газа на его объем постоянно, если температура газа не меняется. Формулу закона можно записать иначе
Изобарным процессом называются изменения состояния газа, протекающие при постоянном давлении. Изобарный процесс в идеальном газе подчиняется закону Гей-Люсака:
Для газа данной массы отношение объема газа к его температуре постоянно, если давление газа не меняется. Формулу закона можно записать иначе – параметры газа в разные моменты времени
- график, отражающий изобарный процесс, называется изобарой. На графиках представлены изобары для разных давлений газа, где р1 меньше р2. Изохорным процессом называются изменения состояния газа, протекающие при постоянном объеме.
Для газа данной массы отношение давления газа к его температуре постоянно, если объем газа не меняется.
8. Теплоемкость идеального газа. Закон Майера. Теплоёмкость тела характеризуется количеством теплоты, необходимой для нагревания этого тела на один градус:
Размерность теплоемкости: [C] = Дж/К. Однако, теплоёмкость – величина неопределённая, поэтому пользуются понятиями удельной и молярной теплоёмкости. Удельная теплоёмкость (Суд) есть количество теплоты, необходимое для нагревания единицы массы вещества на 1 градус [Cуд] = Дж/К. Для газов удобно пользоваться молярной теплоемкостью Cμ- количество теплоты, необходимое для нагревания 1 моля газа на 1 градус:
[Cμ] = Дж/(моль×К). Из п. 1.2 известно, что молярная масса – масса одного моля:
где А – атомная масса; mед - атомная единица массы; NА - число Авогадро; моль μ – количество вещества, в котором содержится число молекул, равное числу атомов в 12 г изотопа углерода 12С. Теплоёмкость термодинамической системы зависит от того, как изменяется состояние системы при нагревании. Если газ нагревать при постоянном объёме, то всё подводимое тепло идёт на нагревание газа, то есть изменение его внутренней энергии. Теплоёмкость при этом обозначается СV. СР – теплоемкость при постоянном давлении. Если нагревать газ при постоянном давлении Р в сосуде с поршнем, то поршень поднимется на некоторую высоту h, то есть газ совершит работу. Следовательно, проводимое тепло затрачивается и на нагревание и на совершение работы. Отсюда ясно, что Итак, проводимое тепло и теплоёмкость зависят от того, каким путём осуществляется передача тепла. Значит, Q и С не являются функциями состояния. Величины СР и СV оказываются связанными простыми соотношениями. Найдём их. Пусть мы нагреваем один моль идеального газа при постоянном объёме (dA = 0). Тогда первое начало термодинамики запишем в виде:
т.е. бесконечно малое приращение количества теплоты Теплоемкость при постоянном объёме будет равна:
В общем случае
так как U может зависеть не только от температуры. Но в случае идеального газа справедлива формула (4.2.4). Из (4.2.4) следует, что
9.
Внутренняя энергия идеального газа является только функцией температуры (и не зависит от V, Р и тому подобных), поэтому формула (4.2.5) справедлива для любого процесса. Для произвольной идеальной массы газа:
При изобарическом процессе, кроме увеличения внутренней энергии, происходит совершение работы газом:
10.
Из основного уравнения молекулярно-кинетической теории
Это уравнение Майера для одного моля газа. Из этого следует, что физический смысл универсальной газовой постоянной в том, что R – численно равна работе, совершаемой одним молем газа при нагревании на один градус в изобарическом процессе. Используя это соотношение, Роберт Майер в 1842 г. вычислил механический эквивалент теплоты: 1 кал = 4,19 Дж. Полезно знать формулу Майера для удельных теплоёмкостей:
или
9. Первое начало термодинамики. Первое начало термодинамики утверждает, что изменение внутренней энергии термодинамической системы (тела) может быть осуществлено двумя путями: путём совершения механической работы и путём теплопередачи. Энергия, переданная системе путём теплопередачи, называется количеством теплоты. Таким образом, количество теплоты может быть определено как разность изменения внутренней энергии системы и механической работы, совершённой над системой:
где – количество теплоты, переданной системе, – изменение внутренней энергии системы при её переходе из первого состояния во второе, – работа, совершённая над системой. Так как работа, совершенная над системой , равна работе, совершенной системой , взятой с обратным знаком: , то первое начало термодинамики может быть сформулировано следующим образом: Теплота , подводимая к системе, идет на изменение ее внутренней энергии и на совершение этой системой работы над внешними телами:
10. Распределение Максвелла. Молекулы газа при своем движении постоянно сталкиваются. Скорость каждой молекулы при столкновении изменяется. Она может возрастать и убывать. Однако среднеквадратичная скорость остается неизменной. Это объясняется тем, что в газе, находящемся при определенной температуре, устанавливается некоторое стационарное, не меняющееся со временем распределение молекул по скоростям, которое подчиняется определенному статистическому закону. Скорость отдельной молекулы с течением времени может меняться, однако доля молекул со скоростями в некотором интервале скоростей остается неизменной. Нельзя ставить вопрос: сколько молекул обладает определенной скоростью. Дело в том, что, хоть число молекул очень велико в любом даже малом объеме, но количество значений скорости сколь угодно велико (как чисел в последовательном ряде), и может случиться, что ни одна молекула не обладает заданной скоростью. Задачу о распределении молекул по скоростям следует сформулировать следующим образом. Пусть в единице объема n молекул. Какая доля молекул имеет скорости от v1 до v1 + Δv? Это статистическая задача. Основываясь на опыте Штерна, можно ожидать, что наибольшее число молекул будут иметь какую-то среднюю скорость, а доля быстрых и медленных молекул не очень велика. Необходимые измерения показали, что доля молекул , отнесенная к интервалу скорости Δv, Максвелл в 1859 г. теоретически на основании теории вероятности определил эту функцию. С тех пор она называется функцией распределения молекул по скоростям или законом Максвелла. Аналитически она выражается формулой , где m – масса молекулы, k – постоянная Больцмана. Установление этой зависимости позволило определить кроме уже известной среднеквадратичной скорости еще две характерные скорости – среднюю и наиболее вероятную. Средняя скорость – это сумма скоростей всех молекул, деленная на общее число всех молекул в единице объема. Средняя скорость, подсчитанная на основании закона Максвелла, выражается формулой
или
Наиболее вероятная скорость – это скорость, вблизи которой на единичный интервал скоростей приходится наибольшее число молекул. Она рассчитывается по формуле: . Сопоставляя все три скорости: 1) наиболее вероятную 2) среднюю 3) среднюю квадратичную
11. Классическая теория теплоемкости. Молярная теплоемкость при постоянном объеме:
Из уравнения Майера найдем молярную теплоемкость при постоянном давлении с учетом (3.46):
Соответственно показатель адиабаты
Для одноатомных газов число степеней свободы i=3. Согласно формул (3.46), (3.47) и (3.48) найдем, что » 12,5 Дж/(моль×К); » 20,8 Дж/(моль×К); g =1,67. Для двухатомных газов число степеней свободы i =5, т.е. » 20,8 Дж/(моль×К); » 29,1 Дж/(моль×К); g =1,4. Для трехатомных молекул газа число степеней свободы i=6, т.е. Cv=3R » 24,9 Дж/(моль×К); Cp=4R » 33,24 Дж/(моль×К); g =1,33. Вывод: теплоемкость идеальных газов согласно классической теории не зависит от температуры. Этот вывод классической теории теплоемкости находится в противоречии с экспериментальными данными. При низких температурах теплоемкость многоатомных газов ведет себя как теплоемкость одноатомных молекул газа, а при повышении температуры теплоемкость их растет быстрее, чем это следует из классической теории. Причина расхождения экспериментальных данных с теоретическими выводами заключается в ограниченности классической теории. Полное объяснение теплоемкости веществ дала квантовая механика. Из квантовой теории следует: вклад в теплоемкость веществ вносят не все, а только некоторые степени свободы в определенных интервалах температур (это положение подтверждено экспериментальными данными). Внутренняя энергия физических систем может принимать не любые значения (как в классической физике), а лишь дискретные, т.е. квантуется. 12. 2 начало термодинамики. Понятие о тепловой машине. Термодинамика – это наука о тепловых процессах, о превращении тепловой энергии. Для описания термодинамических процессов первого начала термодинамики недостаточно. Выражая общий закон сохранения и превращения энергии, первое начало не позволяет определить направление протекания процессов. Исторически второе начало термодинамики возникло из анализа работы тепловых двигателей. Рассмотрим схему теплового двигателя. От термостата с более высокой температурой Т1, называемого нагревателем, за цикл отнимается количество теплоты Q1, а термостату с более низкой температурой Т2, называемому холодильником, за цикл передается количество теплоты Q2 и совершается работа
Чтобы термический коэффициент полезного действия теплового двигателя был В 1824 г. Карно доказал, что для работы теплового двигателя необходимо не менее двух источников теплоты с различными температурами. Невозможность создания вечного двигателя второго рода подтверждается вторым началом термодинамики. Приведем некоторые формулировки второго начала термодинамики:
13. Цикл Карно. В соответствии с первым началом термодинамики (1.2), при осуществлении кругового процесса, из-за возвращения рабочего тела в исходное состояние, его внутренняя энергия за цикл не изменяется. Поэтому совершенная рабочим телом механическая работа равна разности подведенной
Тепловой коэффициент полезного действия (к.п.д.) цикла любой тепловой машины можно рассчитать как отношение полезной работы
Из выражения (1.13) следует, что к.п.д. любого цикла всегда меньше единицы, так как часть полученной от нагревателя теплоты должна передаваться холодильнику. Максимальным тепловым коэффициентом полезного действия обладает цикл Карно, который является обратимым и состоит из следующих друг за другом изотермических и адиабатических процессов. Для организации простейшего кругового процесса достаточно использования двух изотерм и двух адиабат. Возможность осуществления такого циклического процесса связана с тем, что с помощью адиабатического процесса всегда возможен переход между любыми изотермами, а с помощью изотермического - между любыми адиабатами. 14. Идеальные газы. 1. Идеальным газом называется газ, в котором отсутствуют силы межмолекулярного взаимодействия. С достаточной степенью точности газы можно считать идеальными в тех случаях, когда рассматриваются их состояния, далекие от областей фазовых превращений. 2. Для идеальных газов справедливы следующие законы: 3. в) Закон Шарля: при постоянном объеме давление данной массы газа прямо пропорционально его абсолютной температуре: 15. Уравнение Ван-дер-Ваальса.
16. График уравнения Ван-дер-Ваальса.
На этих изотермах хорошо просматривается участок, где давление растёт с ростом объёма. Этот участок не имеет физического смысла. В области, где изотерма делает зигзагообразный изгиб, изобара пересекает её три раза, то есть, имеется три значения объёма при одинаковых значениях параметров и . Это соответствует существованию трёх действительных корней уравнения (2.117). При повышении температуры волнообразный участок уменьшается и превращается в точку (см. точка К на рис. 2.8). Эта точка называется критической, а значения , и в этой точке называются критическими параметрами. Критической точке соответствуют три совпадающих корня уравнения (2.117). При температурах, превышающих критическую, изотермы Ван-дер-Ваальса становятся монотонно убывающими функциями. 17. Общая характеристика строения жидкости. 1. Жидкостями называются тела, которые имеют определенный объем, но не имеют упругости формы. Жидкости отличаются сильным межмолекулярным взаимодействием и, вследствие этого, малой сжимаемостью. Малая сжимаемость жидкостей объясняется тем, что небольшое уменьшение расстояния между молекулами на малых взаимных расстояниях приводит к появлению больших сил межмолекулярного отталкивания. Коэффициент сжимаемости для жидкостей изменяется в пределах от 2*10-6 до 2*10-4 атм-1 18. Смачивание. Капиллярные явления. Смачивание - явление, возникающее при контакте жидкости с поверхностью твердого тела, в результате которого свободная поверхность жидкости искривляется. Если поместить один конец узкой трубки (капилляр) в широкую посуду, наполненную жидкостью, то вследствие смачивания или несмачивание жидкостью стенок капилляра кривизна поверхности жидкости в капилляре становится значительной. Если жидкость смачивает материал капилляра, то внутри его поверхность жидкости - мениск - имеет вогнутую форму, а уровень жидкости внутри капилляра выше открытой поверхности. Если жидкость не смачивает материал капилляра, то мениск имеет выпуклую форму и уровень жидкости внутри капилляра ниже открытой поверхности. Капиллярные явления играют большую роль в природе и технике. Например, влагообмен в почве и растениях осуществляется за счет поднятия воды по тончайшим капиллярам. На капиллярности основано действие гнета, впитывания влаги бетоном и т.д.. |






 где
где – параметры газа в разные моменты времени
– параметры газа в разные моменты времени - график, отражающий изотермический процесс, называется изотермой.
- график, отражающий изотермический процесс, называется изотермой.

 где
где

 где
где – параметры газа в разные моменты времени
– параметры газа в разные моменты времени 



 .
. ,
,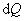 равно приращению внутренней энергии dU.
равно приращению внутренней энергии dU. ,
, ,
,
 ,
, ,
, ,
,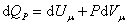 .
. .
. . При изобарическом процессе Р = const.
. При изобарическом процессе Р = const. .
. .
. .
. ,
, .
. ,
,
 .
. .
. ,
, ,
, ,
,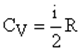 . (3.46)
. (3.46) . (3.47)
. (3.47) . (3.48)
. (3.48)

 , должно быть выполнено условие
, должно быть выполнено условие 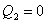 , т.е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Такой двигатель называется вечным двигателем второго рода.
, т.е. тепловой двигатель должен иметь один источник теплоты, а это невозможно. Такой двигатель называется вечным двигателем второго рода.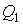 и отведенной
и отведенной  теплоты:
теплоты: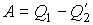 .
.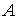 к количеству теплоты
к количеству теплоты  .
.
