 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Микроскопические модели проводимости. Модель Друде.
Лекция 7. Итоги предыдущей лекции. Электрический ток, носители тока, дрейфовая скорость, плотность тока, закон сохранения заряда, закон Ома, закон Джоуля-Ленца. Сторонние силы, ЭДС. Закон Ома для участка цепи с электродвижущей силой. Параллельное и последовательное соединение проводников. Законы Кирхгофа. На прошлой лекции мы с вами получили следующие результаты. Потенциал элементарного диполя
Также нашли формулы для энергии, для момента и силы, действующих на элементарный диполь во внешнем электрическом поле:
Далее мы обобщили понятие дипольный момент на системы зарядов и определили вектор поляризации, который играет важную роль при описании диэлектриков:
Мы показали, что с вектором поляризации связаны поверхностная плотность заряда на поверхности диэлектрика и объемная плотность поверхностного заряда в объеме диэлектрика:
Оказалось, что если ввести вектор электрической индукции
Это оказалось очень удобным, так как в большинстве задач заданы распределения только свободных зарядов (а поляризационные заряды, также как и поля надо найти). После нахождения вектора электрической индукции значение напряженности находится из законов линейного отклика (в простейшей форме):
В заключение мы вывели граничные условия для электрической индукции и напряженности на границе двух диэлектриков:
Теперь мы возвращаемся к теме проводников, но будем изучать немного другой класс физических процессов в них. Раньше мы рассматривали статические явления, то есть электростатику. Мы определяли проводники как тела, в которых любое сколь-угодно слабое электрическое поле вызывает движение зарядов. Отсюда мы пришли к выводу, что в статической ситуации электрическое поле
Рис.1.
На рисунке 1а изображен проводник в виде цилиндра. Предположим, что вдоль оси проводника (слева направо) приложено электрическое поля Электрическим током называют упорядоченное движение зарядов в проводнике. Сами заряды называют носителями тока. Что за частицы переносят ток? В большинстве веществ носителями тока являются электроны: это проводники первого рода. В ряде веществ (в электролитах) ток может осуществляться ионами: это проводники второго рода. Бывают и смешанные случаи. В некоторых случаях удобно считать, что носителями тока являются особые возбуждения электронов (дырки). Важным моментом является характер движения носителей тока в проводнике. Мы знаем, что на заряд в электрическом поле действует сила. Казалось бы, под действием этой силы заряды должны двигаться равноускоренно. Но опыт скорее согласуется с равномерным движением носителей тока в постоянном электрическом поле. Как разрешить это противоречие? На самом деле носители тока под действием постоянного электрического поля действительно двигаются равноускоренно. Но не надо забывать, что носители тока двигаются не в вакууме, а внутри твердого тела, где они могут сталкиваться с атомами решетки, с примесями и так далее. При столкновении они отдают приобретенный импульс (и энергию) решетке: как бы останавливаются. Затем снова начинают двигаться равноускоренно. В среднем получается образ равномерного потока носителей тока. Такое движение носителей называют дрейфовым. В дальнейшем под скоростью мы будем понимать не истинную скорость, а именно дрейфовую скорость Еще несколько понятий. Расстояние, которое проходит носитель тока между двумя последовательными столкновениями, называют длиной свободного пробега, соответствующий период времени: временем свободного пробега. Как вы думаете: каково соотношение между длиной свободного пробега и межатомным расстоянием? Противоречия классической картины переноса тока. Почему одни вещества диэлектрики, другие проводники, а третью полупроводники. А как описать сверхпроводники? Об этом поговорим в конце лекции, а теперь продолжим введение основных понятий для описания равномерного (дрейфового) движения зарядов в проводниках. Определим такие характеристики равномерного дрейфового движения зарядов как сила тока и плотность тока. Вернемся к рисунку 1, на котором выделим объем с поперечным сечением
А заряд в единицу времени и через единицу площади:
где под
Ясно также как обобщить выражение (9) на случай носителей нескольких типов:
Фундаментальным законом природы является закон сохранения электрического заряда. Выведем его математическое выражение. Для этого рассмотрим рисунок 2:
Рис.2.
Для производной от заряда внутри поверхности (если принять, что заряд не рождается и не исчезает) получаем
Для стационарных явлений, которые мы будем рассматривать в ближайшее время, этот закон можно записать так
Для создания стационарного тока надо создавать и поддерживать стационарное значение напряженности электрического поля. Опыт показывает, что в этих условиях плотность тока пропорциональна величине напряженности электрического поля:
Этот закон называется законом Ома в дифференциальной форме. Он имеет очень большое значение в теории электричества, хотя и не является фундаментальным законом природы. Величина Из (14) для однородного проводника нетрудно получить выражение для закона Ома в интегральной форме:
При движении носителей тока вся энергия, приобретаемая ими, передается решетке (переходит в энергию колебаний решетки, в тепловую энергию). Подсчитаем эту энергию:
Таким образом, объемная мощность потерь (энергия в тепло в единицу времени и в единичном объеме) равна:
Это закон Джоуля-Ленца в дифференциальной форме. Нетрудно для проводника конечных размеров получить выражение в виде:
Это закон Джоуля-Ленца в интегральной форме. Теперь мы более подробно рассмотрим вопрос, а как создать постоянное поле в проводнике, то есть, как поддержать стационарное значение электрического тока? Ясно, что мы должны иметь устройство, которое уничтожает возникающее перераспределение заряда (возникающее под действием тока) и поддерживает стационарную ситуацию. Ясно также, что перераспределять заряды должны силы неэлектрического происхождения. Действительно, если существуют только силы электрические, то для постоянного поля должно быть:
Но это означает, что работа электрических сил равна нулю. Откуда же берется энергия на омические потери (смотри закон Джоуля-Ленца). Определим напряженность сторонних сил:
Тогда закон ома будет выглядеть так:
Вот пример (механического) устройства разделяющего заряды:
Для него напряженность сторонних сил равна
Химическим источником может быть цинковая и медная пластинка в серной кислоте (гальванический источник тока). К каким следствиям приведет обобщение закона Ома на случай сторонних сил. Из соотношения (20) получаем (
Последнее соотношение можно записать так:
Здесь геометрия цепи такова:
Соотношение (22) называется законом Ома для участка цепи, содержащего ЭДС (электродвижущую силу). Именно на участке
Соотношение (23) позволяет решать простейшие задачи по расчету электрических цепей. Но для более сложных случаев их явно недостаточно. В этом случае существует метод, основанный на двух законах Кирхгофа. Сущность этих законов очень проста. Первый закон Кирхгофа выражает закон сохранения заряда в применении к узлу цепи (узлом называем любую точку цепи, в которой соединяется два или более проводников). Первый закон Кирхгофа формулируется так: алгебраическая сумма токов для любого узла равна нулю:
где входящие токи берутся со знаком
Слева знак Еще один полезный рецепт. Начиная расчет цепи, ставим стрелки у отдельных резисторов не задумываясь (произвольно, от этого ответ зависеть не будет). Направления обходов контуров также выбираем произвольно. Затем выписываем уравнения законов Кирхгофа и решаем систему линейных уравнений. Число уравнений первого закона Кирхгофа равно числу узлов с тремя и более проводниками минус 1. Число контуров: наиболее сложный вопрос. Не следует писать лишние уравнения для составных контуров, оставляем только элементарные контуры, которые не получаются из других контуров их объединением. Решить задачу:
При решении задач с помощью законов Кирхгофа получается Теперь рассмотрим токи в объемных проводниках. Из закона сохранения заряда для стационарного случая получаем и однородной среды:
То есть сначала решаем задачу о нахождении потенциала при заданных потенциалах проводников (электродов). После этого вычисляем плотности тока по дифференциальному закону Ома. Мы рассмотрели процессы с постоянными токами. Близкие к ним задачи с переменными токами при следующих приближениях: а) мгновенные токи одинаковы во всех сечениях проводов, б) мгновенное значение электрического поля определятся мгновенным значением заряда конденсатора как в электростатике. Такие условия называются условиями квазистационарности. Микроскопические модели проводимости. Модель Друде. Модель Друде основана на следующих предположениях: (а) Электроны имеют (характеризуются) временем рассеяния (б) после рассеяния импульс полностью теряется, становится равным Тогда среднее значение импульса в момент времени
В стационарном случае:
Откуда получаем, удельную проводимость:
|



 :
: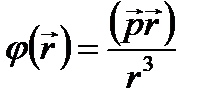 (1)
(1) ,
,  ,
,  (2)
(2) (3)
(3) (4)
(4)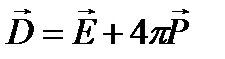 , то теорема Гаусса для него выражается только через внешние (свободные) заряды:
, то теорема Гаусса для него выражается только через внешние (свободные) заряды: ,
,  (5)
(5) ,
, 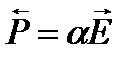 ,
, 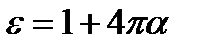 (6)
(6) (7)
(7) и плотность зарядов
и плотность зарядов 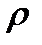 внутри проводника равны нулю: возможно только наличие поверхностных зарядов на поверхности проводника. Но это вовсе не означает, что нельзя создать электрическое поле внутри проводника. Для этого достаточно только отказаться от условия неподвижности зарядов. Рассмотрим рисунок 1, который будет использован в этой лекции несколько раз
внутри проводника равны нулю: возможно только наличие поверхностных зарядов на поверхности проводника. Но это вовсе не означает, что нельзя создать электрическое поле внутри проводника. Для этого достаточно только отказаться от условия неподвижности зарядов. Рассмотрим рисунок 1, который будет использован в этой лекции несколько раз
 .
. и длиной
и длиной  . Все заряды в выделенном объеме за время
. Все заряды в выделенном объеме за время  пересекут правое (заштрихованное основание). Поэтому полный заряд, прошедший через это сечение за указанное время равен (
пересекут правое (заштрихованное основание). Поэтому полный заряд, прошедший через это сечение за указанное время равен (  -заряд,
-заряд,  - концентрация):
- концентрация):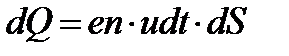 (8)
(8) . В векторном виде имеем:
. В векторном виде имеем: (9)
(9) понимается вектор с направлением дрейфовой скорости
понимается вектор с направлением дрейфовой скорости  и величиной, равной количеству заряда, протекающего в единицу времени через единичную площадку, ориентированную перпендикулярно дрейфовой скорости. Этот вектор называется вектором плотности тока. С учетом этого определения легко получить, что для тока через поверхность
и величиной, равной количеству заряда, протекающего в единицу времени через единичную площадку, ориентированную перпендикулярно дрейфовой скорости. Этот вектор называется вектором плотности тока. С учетом этого определения легко получить, что для тока через поверхность  (в единицу времени) имеем выражение (помните выражение поток вектора):
(в единицу времени) имеем выражение (помните выражение поток вектора):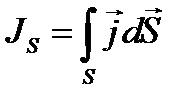 (10)
(10) (11)
(11)
 (12)
(12) (13)
(13) (14)
(14) называется удельной проводимостью, а обратная величина
называется удельной проводимостью, а обратная величина  удельным сопротивлением. Каковы размерности
удельным сопротивлением. Каковы размерности 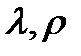 в Гауссовой системе единиц?
в Гауссовой системе единиц? (15)
(15)
 (16)
(16) (17)
(17) (18)
(18)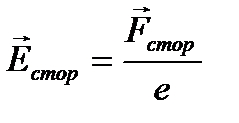 (19)
(19) (20)
(20)
 (21)
(21) ):
):
 (22)
(22)
 действуют сторонние силы и придают носителям тока энергию (которая переходит в Джоулево тепло). С экспериментальной точки зрения ЭДС можно померить вольтметром как разность потенциалов при разомкнутой цепи
действуют сторонние силы и придают носителям тока энергию (которая переходит в Джоулево тепло). С экспериментальной точки зрения ЭДС можно померить вольтметром как разность потенциалов при разомкнутой цепи (23)
(23) (24)
(24) , а выходящие со знаком
, а выходящие со знаком  . Перейдем ко второму закону Кирхгофа. Выделим в цепи замкнутый контур и возьмем для него сумму выражений (22):
. Перейдем ко второму закону Кирхгофа. Выделим в цепи замкнутый контур и возьмем для него сумму выражений (22): (25)
(25)
 уравнений. Число уравнений можно уменьшить, если использовать контурные токи (привести пример).
уравнений. Число уравнений можно уменьшить, если использовать контурные токи (привести пример). (26)
(26) (среднее время жизни без рассеяния). Вероятность рассеяния в единицу времени равна
(среднее время жизни без рассеяния). Вероятность рассеяния в единицу времени равна  .
. .
. будет равно:
будет равно: (27)
(27) (28)
(28) (29)
(29)