ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ Основные формулы
• Уравнение гармонических колебаний
где х — смещение колеблющейся точки от положения равновесия; • Угловая частота колебаний
где ν и Т — частота и период колебаний. • Скорость точки, совершающей гармонические колебания,
• Ускорение при гармоническом колебании
• Амплитуда А результирующего колебания, полученного при сложении двух колебаний с одинаковыми частотами, происходящих по одной прямой, определяется по формуле
где a1и А2— амплитуды составляющих колебаний; φ1 и φ2— их начальные фазы. • Начальная фаза φ результирующего колебания может быть найдена из формулы
• Частота биений, возникающих при сложении двух колебаний, происходящих по одной прямой с различными, но близкими по значению частотами ν1 и ν2,
• Уравнение траектории точки, участвующей в двух взаимно перпендикулярных колебаниях с амплитудами A1 и A2 и начальными фазами φ1 и φ2,
Если начальные фазы φ1 и φ2 составляющих колебаний одинаковы, то уравнение траектории принимает вид
т. е. точка движется по прямой. В том случае, если разность фаз
т. е. точка движется по эллипсу. • Дифференциальное уравнение гармонических колебаний материальной точки
• Полная энергия материальной точки, совершающей гармонические колебания,
• Период колебаний тела, подвешенного на пружине (пружинный маятник),
где m — масса тела; k — жесткость пружины. Формула справедлива для упругих колебаний в пределах, в которых выполняется закон Гука (при малой массе пружины в сравнении с массой тела). Период колебаний математического маятника
где l — длина маятника; g — ускорение свободного падения. Период колебаний физического маятника
где J — момент инерции колеблющегося тела относительно оси колебаний; а — расстояние центра масс маятника от оси колебаний;
Приведенные формулы являются точными для случая бесконечно малых амплитуд. При конечных амплитудах эти формулы дают лишь приближенные результаты. При амплитудах не более Период крутильных колебаний тела, подвешенного на упругой нити,
где J — момент инерции тела относительно оси, совпадающей с упругой нитью; k — жесткость упругой нити, равная отношению упругого момента, возникающего при закручивании нити, к углу, на который нить закручивается. • Дифференциальное уравнение затухающих колебаний где r — коэффициент сопротивления; δ — коэффициент затухания:
• Уравнение затухающих колебаний
где A (t) — амплитуда затухающих колебаний в момент t; ω — их угловая частота. • Угловая частота затухающих колебаний
О Зависимость амплитуды затухающих колебаний от времени
где А0 — амплитуда колебаний в момент t=0. • Логарифмический декремент колебаний
где A (t) и A (t+T) — амплитуды двух последовательных колебаний, отстоящих по времени друг от друга на период. • Дифференциальное уравнение вынужденных колебаний
где • Амплитуда вынужденных колебаний
• Резонансная частота и резонансная амплитуда Примеры решения задач Пример 1.Точка совершает колебания по закону x(t)= x(0)= Решение. Воспользуемся уравнением движения и выразим смещение в момент t=0 через начальную фазу:
* В приведенных ранее формулах гармонических колебаний та же величина обозначалась просто ω (без индекса 0). Подставим в это выражение заданные значения x(0) и А: φ=
Для того чтобы решить, какое из этих значений угла φ удовлет-
Подставив в это выражение значение t=0 и поочередно значения
По найденному значению φ постро- Решение. 1. Уравнение гармонического колебания имеет вид
а формулу скорости получим, взяв первую производную по времени от смещения:
Чтобы выразить скорость через смещение, надо исключить из формул (1) и (2) время. Для этого возведем оба уравнения в квадрат, разделим первое на А2, второе на A2 ω 2 и сложим:
Решив последнее уравнение относительно υ, найдем
Выполнив вычисления по этой формуле, получим
Знак плюс соответствует случаю, когда направление скорости совпадает с положительным направлением оси х, знак минус — когда направление скорости совпадает с отрицательным направлением оси х. Смещение при гармоническом колебании кроме уравнения (1) может быть определено также уравнением
Повторив с этим уравнением такое же решение, получим тот же ответ. 2. Силу действующую на точку, найдем по второму закону Ньютона:
где а — ускорение точки, которое получим, взяв производную по времени от скорости:
Подставив выражение ускорения в формулу (3), получим
Отсюда максимальное значение силы
Подставив в это уравнение значения величин π, ν, т и A, найдем
3. Полная энергия колеблющейся точки есть сумма кинетической и потенциальной энергий, вычисленных для любого момента времени. Проще всего вычислить полную энергию в момент, когда кинетическая энергия достигает максимального значения. В этот момент потенциальная энергия равна нулю. Поэтому полная энергия E колеблющейся точки равна максимальной кинетической энергии Tmax:
Максимальную скорость определим из формулы (2), положив
Подставив значения величин в эту формулу и произведя вычисления, получим
или Пример 3. На концах тонкого стержня длиной l = 1 м и массой m3=400 г укреплены шарики малых размеров массами m1=200 ги m2=300г. Стержень колеблется около горизонтальной оси, перпен-
дикулярной стержню и проходящей через его середину (точка О на рис. 6.2). Определить период Т колебаний, совершаемых стержнем. Решение. Период колебаний физического маятника, каким является стержень с шариками, определяется соотношением
Момент инерции данного маятника равен сумме моментов инерции шариков J1 и J2 и стержня J3:
Принимая шарики за материальные точки, выразим моменты их инерции: Так как ось проходит через середину стержня, то
Произведя вычисления по этой формуле, найдем
Рис. 6.2 Масса маятника состоит из масс шариков и массы
Расстояние lС центра масс маятника от оси колебаний найдем, исходя из следующих соображений. Если ось х направить вдоль стержня и начало координат совместить с точкой О, то искомое расстояние l равно координате центра масс маятника, т. е.
Подставив значения величин m1, m2, m, l и произведя вычисления, найдем
Произведя расчеты по формуле (1), получим период колебаний физического маятника:
Пример 4.Физический маятник представляет собой стержень
маятника проходит через середину стержня перпендикулярно ему (рис. 6.3). Определить период Т колебаний такого маятника. Решение. Период колебаний физического маятника определяется по формуле
где J — момент инерции маятника относительно оси колебаний; т — его масса; lC — расстояние от центра масс маятника до оси колебаний. Момент инерции маятника равен сумме моментов инерции стержня J1и обруча J2:
Момент инерции стержня относительно оси,
Момент инерции обруча найдем, восполь-
Подставив выражения J1 и J2 в формулу (2), найдем момент инерции маятника относительно оси вращения:
Расстояние lС от оси маятника до его центра масс равно
Подставив в формулу (1) выражения J, lс и массы маятника
После вычисления по этой формуле получим T=2,17 с. Пример 5.Складываются два колебания одинакового направле- баний. 2. Найти амплитуду А и начальную фазу φ результирующего колебания. Написать уравнение результирующего колебания. Решение. 1. Уравнение гармонического колебания имеет вид
Преобразуем уравнения, заданные в условии задачи, к такому же виду:
Из сравнения выражений (2) с равенством (1) находим начальные фазы первого и второго колебаний:
2. Для определения амплитуды А результирующего колебания удобно воспользоваться векторной диаграммой, представленной на рис.6.4. Согласно теореме косинусов, получим
где
Подставим значения А1, А2и A=2,65 см. Тангенс начальной фазы φ результирующего колебания опреде-
Подставим значения А1, А2, φ 1, φ 2 и произведем вычисления:
Так как угловые частоты складываемых колебаний одинаковы, Пример 6.Материальная точка участвует одновременно в двух взаимно перпендикулярных гармонических колебаниях, уравнения которых
где a1=1 см, A2=2 см, Решение. Чтобы найти уравнение траектории точки, исключим время t из заданных уравнений (1) и (2). Для этого восполь- зуемся формулой
Так как согласно формуле (1)
Полученное выражение представляет собой уравнение параболы, ось которой совпадает с осью Ох. Из уравнений (1) и (2) следует, что смещение точки по осям координат ограничено и заключено в пределах от —1 до +1 см по оси Ох и от —2 до +2 см по оси Оу. Для построения траектории найдем по уравнению (3) значения у, соответствующие ряду значений х, удовлетворяющих условию
Начертив координатные оси и выбрав масштаб, нанесем на плоскость хОу найденные точки. Соединив их плавной кривой, получим траекторию точки, совершающей колебания в соответствии с уравнениями движения (1) и (2) (рис. 6.5).
Для того чтобы указать направление движения точки, проследим за тем, как изменяется ее положение с течением времени. В начальный момент t=0 координаты точки равны x(0)=1 см и y(0)=2 см. В последующий момент времени, например при t1=l с, координаты точек изменятся и станут равными х (1)= —1 см, y(t)=0. Зная положения точек в начальный и последующий (близкий) моменты времени, можно указать направление движения точки по траектории. На рис. 6.5 это направление движения указано стрелкой (от точки А к началу координат). После того как в момент t2 = 2 с колеблющаяся точка достигнет точки D, она будет двигаться в обратном направлении. Задачи Кинематика гармонических колебаний 6.1. Уравнение колебаний точки имеет вид 6.2.Определить период Т, частоту v и начальную фазу φ колебаний, заданных уравнением 6.3.Точка совершает колебания по закону 6.4.Точка совершает колебания .по закону 6.5.Точка совершает колебания по закону 6.6.Точка совершает колебания с амплитудой A=4 см и периодом Т=2 с. Написать уравнение этих колебаний, считая, что в 6.7.Точка равномерно движется по окружности против часовой стрелки с периодом Т=6 с. Диаметр d окружности равен 20 см. Написать уравнение движения проекции точки на ось х, проходящую через центр окружности, если в момент времени, принятый за начальный, проекция на ось х равна нулю. Найти смещение х, скорость 6.8.Определить максимальные значения скорости 6.9.Точка совершает колебания по закону 6.10.Точка совершает гармонические колебания. Наибольшее 6.11.Максимальная скорость 6.12.Точка совершает колебания по закону 6.13. Колебания точки происходят по закону Сложение колебаний 6.14.Два одинаково направленных гармонических колебания одного периода с амплитудами A1=10 см и A2=6 см складываются в одно колебание с амплитудой А=14 см. Найти разность фаз 6.15.Два гармонических колебания, направленных по одной прямой и имеющих одинаковые амплитуды и периоды, складываются в одно колебание той же амплитуды. Найти разность фаз 6.16.Определить амплитуду А и начальную фазу ф результи 6.17. Точка участвует в двух одинаково направленных колебаниях: 6.18. Складываются два гармонических колебания одного на 6.19.Складываются три гармонических колебания одного направления с одинаковыми периодами Т1=Т2=Т3=2 с и амплитудами A1=A2=A3=3 см. Начальные фазы колебаний φ1=0, φ2=π/3, φ3=2π/3. Построить векторную диаграмму сложения амплитуд. Определить из чертежа амплитуду А и начальную фазу φ результирующего колебания. Найти его уравнение. 6.20.Складываются два гармонических колебания одинаковой 6.21. Два камертона звучат одновременно. Частоты ν1 и ν2 их колебаний соответственно равны 440 и 440,5 Гц. Определить период Т биений. 6.22. Складываются два взаимно перпендикулярных колебания, 6.23. Точка совершает одновременно два гармонических колебания, происходящих по взаимно перпендикулярным направлениям 6.24. Точка совершает одновременно два гармонических колебания одинаковой частоты, происходящих по взаимно перпендикулярным направлениями выражаемых уравнениями: 1) Найти (для восьми случаев) уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: А=2 см, A1=3 см, А2=1см; φ1=π/2, φ2=π. 6.25. Точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 6.26. Точка одновременно совершает два гармонических колебания, происходящих по взаимно перпендикулярным направлениям 6.27. Движение точки задано уравнениями 6.28. Материальная точка участвует одновременно в двух взаимно перпендикулярных колебаниях, выражаемых уравнениями 6.29. Точка участвует одновременно в двух гармонических колебаниях, происходящих по взаимно перпендикулярным направлениям описываемых уравнениями: 1) Найти уравнение траектории точки, построить ее с соблюдением масштаба и указать направление движения. Принять: A=2 см; A1=з см. 6.30. Точка участвует одновременно в двух взаимно перпенди- y=A2 sin 0,5ωt, где A1=2см, A2=3 см. Найти уравнение траектории точки и построить ее, указав направление движения. 6.31.Смещение светящейся точки на экране осциллографа является результатом сложения двух взаимно перпендикулярных колебаний, которые описываются уравнениями: 1) х=А sin 3ωt и у=A sin 2ωt; 2) х=А sin 3ωt и y=A cos 2ωt; 3) х=А sin 3ωt и y=A cos ωt. Применяя графический метод сложения и соблюдая масштаб, построить траекторию светящейся точки на экране. Принять А=4 см. Динамика гармонических колебаний. Маятники 6.32.Материальная точка массой т=50 г совершает колебания, уравнение которых имеет вид х=А cos ωt, где А = 10 см, ω=5 с-1. Найти силу F, действующую на точку, в двух случаях: 1) в момент, когда фаза ωt=π/3; 2) в положении наибольшего смещения точки. 6.33.Колебания материальной точки массой т=0,1 г происходят согласно уравнению х=A cos ωt, где A=5 см; ω=20 с-1. Определить максимальные значения возвращающей силы Fmax и кинетической энергии Тmах. 6.34.Найти возвращающую силу F в момент t=1 с и полную энергию Е материальной точки, совершающей колебания по закону х=А cos ωt, где А = 20 см; ω=2π/3 с-1. Масса т материальной точки равна 10 г. 6.35.Колебания материальной точки происходят согласно уравнению х=A cos ωt, где A=8 см, ω=π/6 с-1. В момент, когда возвращающая сила F в первый раз достигла значения —5 мН, потенциальная энергия П точки стала равной 100 мкДж. Найти этот момент времени t и соответствующую ему фазу ωt. 6.36.Грузик массой m=250 г, подвешенный к пружине, колеблется по вертикали с периодом Т=1 с. Определить жесткость k пружины. 6.37. К спиральной пружине подвесили грузик, в результате чего пружина растянулась на х=9 см. Каков будет период Т колебаний грузика, если его немного оттянуть вниз и затем отпустить? 6.38.Гиря, подвешенная к пружине, колеблется по вертикали с амплитудой A =4 см. Определить полную энергию Е колебаний гири, если жесткость k пружины равна 1 кН/м. 6.39.Найти отношение длин двух математических маятников, если отношение периодов их колебаний равно 1,5. 6.40. Математический маятник длиной l=1м установлен в лифте. Лифт поднимается с ускорением а=2,5 м/с2. Определить период Т колебаний маятника. 6.41. На концах тонкого стержня длиной l=30 см укреплены одинаковые грузики по одному на каждом конце. Стержень с грузиками колеблется около горизонтальной оси, проходящей через точку, удаленную на d=10 см от одного из концов стержня. Определить приведенную длину L и период Т колебаний такого физического маятника. Массой стержня пренебречь. 6.42. На стержне длиной l=30 см укреплены два одинаковых грузика: один — в середине стержня, другой — на одном из его концов. Стержень с грузиком колеблется около горизонтальной оси, проходящей через свободный конец стержня. Определить приведенную длину L и период Т колебаний такой системы. Массой стержня пренебречь. 6.43. Система из трех грузов, соединенных стержнями длиной l=30 см (рис. 6.6), колеблется относительно горизонтальной оси, проходящей через точку О перпендикулярно плоскости чертежа. Найти период Т колебаний системы. Массами стержней пренебречь, грузы рассматривать как материальные точки. 6.44. Тонкий обруч, повешенный на гвоздь, вбитый горизонтально в стену, колеблется в плоскости, параллельной стене. Радиус R обруча равен 30 см. Вычислить период Т колебаний обруча.
6.45. Однородный диск радиусом R=30 см колеблется около горизонтальной оси, проходящей через одну из образующих цилиндрической поверхности диска. Каков период Т его колебаний? 6.46. Диск радиусом R=24см колеблется около горизонтальной оси, проходящей через середину одного из радиусов перпендикулярно плоскости диска. Определить приведенную длину L и период Т колебаний такого маятника. 6.47. Из тонкого однородного диска радиусом R=20 см вырезана часть, имеющая вид круга радиусом r=10см, так, как это показано на рис. 6.7. Оставшаяся часть диска колеблется относительно горизонтальной оси О, совпадающей с одной из образующих цилиндрической поверхности диска. Найти период Т колебаний такого маятника. 6.48. Математический маятник длиной l1=40 см и физический маятник в виде тонкого прямого стержня длиной l2=60 см синхронно колеблются около одной и той же горизонтальной оси. Определить расстояние а центра масс стержня от оси колебаний. 6.49.Физический маятник в виде тонкого прямого стержня длиной l=120 см колеблется около горизонтальной оси, проходящей перпендикулярно стержню через точку, удаленную на некоторое расстояние а от центра масс стержня. При каком значении а период Т колебаний имеет наименьшее значение? 6.50. Физический маятник представляет собой тонкий однородный стержень массой т с укрепленным на нем маленьким шариком массой т. Маятник совершает колебания около горизонтальной оси, проходящей через точку О на стержне. Определить период Т гармонических колебаний маятника для случаев а, б, в, г, изображенных на рис. 6.8. Длина l стержня равна 1 м. Шарик рассматривать как материальную точку.
6.51.Физический маятник представляет собой тонкий однородный стержень массой т с укрепленными на нем двумя маленькими шариками массами т и 2т. Маятник совершает колебания около горизонтальной оси, проходящей через точку О на стержне. Определить частоту ν гармонических колебаний маятника для случаев а, б, в, г, изображенных на рис. 6.9. Длина l стержня равна 1 м. Шарики рассматривать как материальные точки. 6.52.Тело массой т=4 кг, закрепленное на горизонтальной оси, совершало колебания с периодом T1=0,8 с. Когда на эту ось был насажен диск так, что его ось совпала с осью колебаний тела, период T2 колебаний стал равным 1,2 с. Радиус R диска равен 20 см, масса его равна массе тела. Найти момент инерции J тела относительно оси колебаний. 6.53.Ареометр массой т=50 г, имеющий трубку диаметром d= 1 см, плавает в воде. Ареометр немного погрузили в воду и затем предоставили самому себе, в результате чего он стал совершать гармонические колебания. Найти период Т этих колебаний. 6.54. В открытую с обоих концов U-образную трубку с площадью поперечного сечения S=0,4 см2 быстро вливают ртуть массой т=200 г. Определить период Т колебаний ртути в трубке. 6.55.Набухшее бревно, сечение которого постоянно по всей длине, погрузилось вертикально в воду так, что над водой находится лишь малая (по сравнению с длиной) его часть. Период Т колебаний бревна равен 5 с. Определить длину l бревна. Затухающие колебания 6.56.Амплитуда затухающих колебаний маятника за время t1=5 мин уменьшилась в два раза. За какое время t2, считая от начального момента, амплитуда уменьшится в восемь раз? 6.57.За время t=8 мин амплитуда затухающих колебаний маятника уменьшилась в три раза. Определить коэффициент затухания δ. 6.58. Амплитуда колебаний маятника длиной l=1м за время t=10 мин уменьшилась в два раза. Определить логарифмический декремент колебаний Θ. 6.59.Логарифмический декремент колебаний Θ маятника равен 0,003. Определить число N полных колебаний, которые должен сделать маятник, чтобы амплитуда уменьшилась в два раза. 6.60.Гиря массой т=500 г подвешена к спиральной пружине жесткостью k=20 Н/м и совершает упругие колебания в некоторой среде. Логарифмический декремент колебаний Θ=0,004. Определить число N полных колебаний, которые должна совершить гиря, чтобы амплитуда колебаний уменьшилась в n=2 раза. За какое время t произойдет это уменьшение? 6.61.Тело массой т=5 г совершает затухающие колебания. В течение времени t=50с тело потеряло 60 % своей энергии. Определить коэффициент сопротивления b. 6.62.Определить период Т затухающих колебаний, если период Т0 собственных колебаний системы равен 1 с и логарифмический декремент колебаний Θ=0,628.
6.63. Найти число N полных колебаний системы, в течение которых энергия системы уменьшилась в n=2 раза. Логарифмический декремент колебаний Θ=0,01.
6.64.Тело массой т=1 кг находится в вязкой среде с коэффициентом сопротивления b=0,05 кг/с. С помощью двух одинаковых пружин жесткостью k=50 Н/м каждое тело удерживается в положении равновесия, пружины при этом не деформированы (рис. 6.10). Тело сместили от положения равновесия и отпустили. Определить: 1) коэффициент затухания δ; 2) частоту ν колебаний; 3) логарифмический декремент колебаний Θ; 4) число N колебаний, по прошествии которых амплитуда уменьшится в е раз. Вынужденные колебания. Резонанс 6.65.Под действием силы тяжести электродвигателя консольная балка, на которой он установлен, прогнулась на h=1 мм. При какой частоте вращения п якоря электродвигателя может возникнуть опасность резонанса? 6.66. Вагон массой т=80 т имеет четыре рессоры. Жесткость k пружин каждой рессоры равна 500 кН/м. При какой скорости υвагон начнет сильно раскачиваться вследствие толчков на стыках рельс, если длина l рельса равна 12,8 м? 6.67.Колебательная система совершает затухающие колебания с частотой ν=1000 Гц. Определить частоту ν0 собственных колебаний, если резонансная частота νpeз=998 Гц. 6.68.Определить, на сколько резонансная частота отличается от частоты ν0=l кГц собственных колебаний системы, характеризуемой коэффициентом затухания δ=400 с-1. 6.69.Определить логарифмический декремент колебаний Θ колебательной системы, для которой резонанс наблюдается при частоте, меньшей собственной частоты ν0=10 кГц на Δν=2 Гц. 6.70.Период Т0 собственных колебаний пружинного маятника равен 0,55 с. В вязкой среде период Т того же маятника стал равным 0,56 с. Определить резонансную частоту ν peз колебаний. 6.71.Пружинный маятник (жесткость k пружины равна 10 Н/м, масса т груза равна 100 г) совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r=2·10-2 кг/с. Определить коэффициент затухания δ и резонансную амплитуду Aрез, если амплитудное значение вынуждающей силы F0=10 мН. 6.72.Тело совершает вынужденные колебания в среде с коэффициентом сопротивления r=1г/с. Считая затухание малым, определить амплитудное значение вынуждающей силы, если резонансная амплитуда Aрез=0,5 см и частота ν 0 собственных колебаний равна 10 Гц. 6.73.Амплитуды вынужденных гармонических колебаний при частоте ν1=400 Гц и ν2=600 Гц равны между собой. Определить резонансную частоту νpeз. Затуханием пренебречь. 6.74. К спиральной пружине жесткостью k=10Н/м подвесили грузик массой т=10 г и погрузили всю систему в вязкую среду. Приняв коэффициент сопротивления b равным 0,1 кг/с, определить: 1) частоту ν0 собственных колебаний; 2) резонансную частоту νpeз; 3) резонансную амплитуду Aрез, если вынуждающая сила изменяется по гармоническому закону и ее амплитудное значение F0= =0,02 Н; 4) отношение резонансной амплитуды к статическому смещению под действием силы F0. 6.75.Во сколько раз амплитуда вынужденных колебаний будет меньше резонансной амплитуды, если частота изменения вынуждающей силы будет больше резонансной частоты: 1) на 10 %? 2) в два раза? Коэффициент затухания δ в обоих случаях принять равным 0,1 ω0 (ω 0 — угловая частота собственных колебаний). |




 — фаза колебаний в момент t.
— фаза колебаний в момент t. , или
, или  ,
,






 , уравнение
, уравнение
 , или
, или  ,
,



 — приведенная длина физического маятника.
— приведенная длина физического маятника. ошибка в значении периода не превышает 1 %.
ошибка в значении периода не превышает 1 %.
 , или
, или  ,
, ; ω0— собственная угловая частота колебаний *
; ω0— собственная угловая частота колебаний *


 I
I
 , или
, или ,
, — внешняя периодическая сила, действующая на
— внешняя периодическая сила, действующая на

 и
и 
 , где А=2 см. Определить начальную фазу φ, если
, где А=2 см. Определить начальную фазу φ, если см и х,(0)<0. Построить векторную диаграмму для мо-
см и х,(0)<0. Построить векторную диаграмму для мо-
 Отсюда найдем начальную фазу:
Отсюда найдем начальную фазу:

 . Значению аргумента
. Значению аргумента  удовлетворяют
удовлетворяют
 , найдем сначала
, найдем сначала  :
:
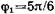 и
и 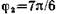 , найдем
, найдем
 Так как всегда A>0 и ω>0, то условию
Так как всегда A>0 и ω>0, то условию  удовлетворяет толь
удовлетворяет толь
 (1)
(1) (2)
(2) , или
, или 

 см/с.
см/с.
 (3)
(3)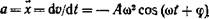 , или
, или

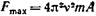

 (4)
(4) :
:  . Подставив выражение скорости в фор-
. Подставив выражение скорости в фор-

 мкДж.
мкДж. (1)
(1) где J — момент инерции маятника относительно оси колебаний; т — его масса; lС — расстояние от центра масс маятника до оси.
где J — момент инерции маятника относительно оси колебаний; т — его масса; lС — расстояние от центра масс маятника до оси. (2)
(2)
 . Подставив полученные выражения J1 , J2 и
. Подставив полученные выражения J1 , J2 и


 , или
, или
 см.
см.
 и массой т1. Горизонтальная ось Oz
и массой т1. Горизонтальная ось Oz (1)
(1)
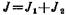 (2).
(2). . В данном случае т=3т1 и
. В данном случае т=3т1 и
 ,
,
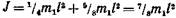


 , найдем период его колебаний:
, найдем период его колебаний:
 ; х2=
; х2= , где А1=1см, A2=2 см,
, где А1=1см, A2=2 см,  с,
с, 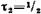 с, ω =
с, ω =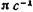 . 1. Определить начальные фазы φ1 и φ 2 составляющих коле-
. 1. Определить начальные фазы φ1 и φ 2 составляющих коле- (1)
(1)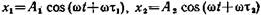 (2)
(2)
 рад и
рад и  рад.
рад. (3)
(3) — разность фаз составляющих колебаний.
— разность фаз составляющих колебаний. , то, подставляя найденные
, то, подставляя найденные рад.
рад. в формулу (3) и
в формулу (3) и , отку-
, отку-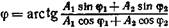
 =
=  рад.
рад.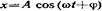 , где A=2,65 см,
, где A=2,65 см,  ,
,  рад.
рад. (1).
(1). (2)
(2) . Найти уравнение траектории точ-
. Найти уравнение траектории точ- . В данном случае
. В данном случае , поэтому
, поэтому
 , то уравнение траекто-
, то уравнение траекто- (3)
(3)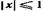 см, и составим таблицу:
см, и составим таблицу:
 ,
, , где ω=2,5π с-1,
, где ω=2,5π с-1, ,
, ; 2) х(0) =
; 2) х(0) =  см и
см и  ; 3) х(0)=2см и
; 3) х(0)=2см и  ; 4)
; 4) и
и  . Построить векторную диаграмму для
. Построить векторную диаграмму для ,
, ; 2) x(0)=
; 2) x(0)=  см и
см и  ; 3) х(0)=
; 3) х(0)=  см и
см и  ;
; см и
см и  . Построить векторную диаграмму для
. Построить векторную диаграмму для ,
, ; φ= π/4 рад. Построить графики зависимости
; φ= π/4 рад. Построить графики зависимости ; 3) ускорения
; 3) ускорения 
 . Определить фазу
. Определить фазу 
 ;
; = —6 см/с и x<0.
= —6 см/с и x<0.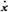 и ускорение
и ускорение  проекции точки в момент t=1с.
проекции точки в момент t=1с. и ускорения
и ускорения  точки, совершающей гармонические колебания с амплитудой А=3см и угловой частотой
точки, совершающей гармонические колебания с амплитудой А=3см и угловой частотой 
 , где А =
, где А = . Определить ускорение
. Определить ускорение  точки в момент времени,
точки в момент времени, =8 см/с.
=8 см/с. =
= точки.
точки. точки, совершающей гармонические колебания, равна10см/с, максимальное ускорение
точки, совершающей гармонические колебания, равна10см/с, максимальное ускорение  =
= . В некоторый момент времени смещение х1точки оказалось равным 5 см. Когда фаза колебаний увеличилась вдвое, смещение х, стало равным 8 см. Найти амплитуду А колебаний.
. В некоторый момент времени смещение х1точки оказалось равным 5 см. Когда фаза колебаний увеличилась вдвое, смещение х, стало равным 8 см. Найти амплитуду А колебаний. .
. = 20 см/с и ускорение
= 20 см/с и ускорение  =—80 см/с2. Найти амплитуду A, угловую частоту ω, период Т колебаний и фазу
=—80 см/с2. Найти амплитуду A, угловую частоту ω, период Т колебаний и фазу  в рассматриваемый момент времени.
в рассматриваемый момент времени. складываемых колебаний.
складываемых колебаний. складываемых колебаний.
складываемых колебаний. и
и 
 , где A1=A2=1 см; ω=π с-1; τ=0,5 с. Найти уравнение результирующего колебания.
, где A1=A2=1 см; ω=π с-1; τ=0,5 с. Найти уравнение результирующего колебания. и
и  , где а1=1см; A2=2 см; ω=
, где а1=1см; A2=2 см; ω= и
и  . Определить амплитуду А и начальную фазу φ результирующего колебания. Найти его уравнение и построить с соблюдением масштаба
. Определить амплитуду А и начальную фазу φ результирующего колебания. Найти его уравнение и построить с соблюдением масштаба и x2=
и x2= . Начертить векторную диаграмму для момента
. Начертить векторную диаграмму для момента и
и  , где
, где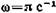 , τ=0,5 с. Найти уравнение траектории
, τ=0,5 с. Найти уравнение траектории и
и  ,
, , τ=1 с. Найти уравнение траектории точки и построить график ее движения.
, τ=1 с. Найти уравнение траектории точки и построить график ее движения. и
и 
 и
и , где A1=2 см, A2=1 см. Найти уравнение траектории
, где A1=2 см, A2=1 см. Найти уравнение траектории и
и  , где А1=
, где А1= и у=
и у=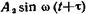 , где A1=10 см, A2=5 см, ω=2 с-1, τ=π/4 с. Найти
, где A1=10 см, A2=5 см, ω=2 с-1, τ=π/4 с. Найти и
и  , где A1=2 см, A2=1 см. Найти
, где A1=2 см, A2=1 см. Найти и
и 

 и
и