 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Задачи на непосредственный подсчёт вероятностей.
Основные понятия. Непосредственный подсчёт вероятностей
Событием(или «случайным событием») называется всякий факт или его отсутствие. Событие называется случайным, если при выполнении комплекса условий оно может произойти, а может и не произойти. Вероятностью события называется численная мера степени объективной возможности этого события. Вероятность события А обозначается Достоверным называется событие А, которое в результате опыта непременно должно произойти.
Невозможным называется событие В, которое в результате опыта не может произойти.
Вероятность любого события А заключена между нулём и единицей: Полной группой событий (схемой событий) называется несколько событий таких, что в результате опыта непременно должно произойти хотя бы одно из них. Несколько событий в данном опыте называются несовместными, если никакие два из них не могут появиться вместе. Несколько событий в данном опыте называются равновозможными (равновероятными), если в появлении их нет преимуществ одного перед другим. Если несколько событий: 1) образуют полную группу; 2) несовместны; 3) равновозможны, то они называются случаями («шансами»). Случай называется благоприятным событию, если появление этого случая влечёт за собой появление события. Если результаты опыта сводятся к схеме случаев (то есть событий конечное число, они равновозможны, несовместны и образуют полную группу), то вероятность события А вычисляется по формуле
где
Задачи на непосредственный подсчёт вероятностей. 1. В урне 3 белых и 5 чёрных шаров. Из урны вынимают наугад один шар. Найти вероятность того, что этот шар белый. 2. Из урны, содержащей 4 белых и 3 чёрных шара, вынимают один за другим все шары, кроме одного. Найти вероятность того, что последний оставшийся в урне шар будет белым. 3. Игральная кость бросается один раз. Найти вероятность следующих событий: А – появление чётного числа очков; В – появление не менее 5 очков; С – появление не более 5 очков. 4. На 9 карточках написаны цифры 0,1,2,3,4,5,6,7,8. Две из них вынимаются наугад и укладываются на стол в порядке их появления, затем читается полученное число. Найти вероятность того, что это число чётное. 5. В урне 5 белых и 7 чёрных шаров. Наудачу вынули 3 шара. Какова вероятность того, что они будут белыми? 6. Группа из 25 человек выделяет команду из 4 человек. В группе 5 следопытов и 4 связиста. Какова вероятность того, что в команде будет 2 следопыта и 2 связиста? 7. В коробке 4 красных и 6 зелёных карандашей. Из неё случайно выпало 3. Какова вероятность того, что 2 из них красные? 8. Билет в партер стоит 250 рублей, на бельэтаж – 200 рублей, на ярус – 150 рублей. Найти вероятность того, что взятые наугад 2 билета стоят вместе не дороже 400 рублей? 9. Группа, состоящая из 5 юношей и 7 девушек, распределила по жребию 4 билета на концерт. Какова вероятность того, что в числе счастливцев окажется больше девушек, чем юношей? 10. В урне 4 белых и 5 чёрных шаров. Из урны вынимают сразу 5 шаров. Какова вероятность, что 2 из них белые, а 3 – чёрные? 11. Из урны, содержащей 5 перенумерованных шаров, вынимают один за другим все шары. Найти вероятность того, что номера будут идти по порядку: 1,2,3,4,5? 12. Та же урна, но каждый шар после вынимания возвращается в урну, а его номер записывается. Найти вероятность того, что будет записана последовательность: 1,2,3,4,5. |



 .
.
 .
. .
. ,
, - число всех случаев,
- число всех случаев,  - число благоприятных случаев.
- число благоприятных случаев. - появление герба;
- появление герба; 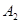 - появление цифры.
- появление цифры. - ни одного попадания;
- ни одного попадания;  - появление карты червонной масти;
- появление карты червонной масти;  - появление карты бубновой масти;
- появление карты бубновой масти;  - появление карты трефовой масти.
- появление карты трефовой масти. - появление одного герба и одной цифры.
- появление одного герба и одной цифры.