 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Приложение производной к исследованию функции
И построению ее графика Методы дифференциального исчисления позволяют исследовать функции и строить их графики. Так, по знаку первой производной в интервале можно определить возрастание (убывание) функции, делать выводы о наличии или отсутствии экстремума функции. По знаку второй производной выделяем интервалы выпуклости (вогнутости) графика функции и точки перегиба ее графика. Справедливы следующие теоремы: 1. Если функция 2. Если дифференцируемая функция 3. Если непрерывная функция 4. Если функция 5. Если вторая производная Построение графика функции значительно облегчается, если известны его асимптоты. Различают 2 вида асимптот: а) Вертикальные, существующие в точках разрыва второго рода. Их уравнения имеют вид б) Наклонные:
В частности, при При исследовании функции и построении ее графика полезно воспользоваться следующей схемой: 1. Найти область определения функции. 2. Найти точки пересечения графика с осями координат, если это возможно. 3. Найти асимптоты графика функции. 4. Найти интервалы монотонности и точки экстремума функции. 5. Найти интервалы выпуклости и вогнутости и точки перегиба графика функции. На основании полученного исследования построить график. Пример 7 Исследовать функцию и построить ее график:
Решение. 1. Область определения.
2. Асимптоты графика: а) вертикальная б) наклонная
3. Найдем производную функции.
Определим знак производной в промежутках:
4. Найдем вторую производную функции.
Точек перегиба графика функции нет.
Вопросы для самопроверки
1. Каковы признаки возрастания и убывания функции? 2. Что называется экстремумом функции? 3. Сформулируйте необходимые и достаточные признаки существования экстремума функции. 4. Как найти интервалы выпуклости и вогнутости кривой и точки перегиба графика функции? 5. Что называется асимптотой кривой? 6. Каких видов бывают асимптоты графика функции и как их найти?
Неопределенный интеграл
Функция Операции дифференцирования и интегрирования взаимнообратны:
поэтому нетрудно получить следующую таблицу интегралов: 1) 2) 3) 4) 5) 6) Не останавливаясь на непосредственном интегрировании по формулам, как на простейшем способе решения примеров, перейдём сразу к более сложным методам. Метод замены переменного
Пусть требуется найти неопределенный интеграл от непрерывной функции Рассмотрим некоторую функцию
В некоторых ситуациях удается подобрать функцию
Другими словами, если подынтегральное выражение может быть записано в форме левой части (4.1.2), то с помощью подстановки
Пример 8 Решение.
Пример 9
На практике часто используется следующая простая формула:
где Пример 10. Пример 11. Пример 12. Интегрирование по частям
Формула интегрирования получается почленным интегрированием формулы производной произведения.
Смысл формулы заключается в том, что производная перебрасывается с одного множителя не другой и интеграл при этом может оказаться проще, чем исходный. Можно выделить по крайней мере два класса интегралов, для которых применима формула интегрирования по частям. I. где При этом формулу приходится применить столько раз, какова степень многочлена.
II. В этом случае, наоборот, следует положить Рассмотрим применение указанной схемы. Пример 13.
Это интеграл первого типа, поэтому:
=
Пример 14. Решение. Это интеграл второго типа, поэтому имеем:
Заметим, что при использовании формулы интегрирования по частям приходится восстанавливать функцию Формула интегрирования по частям может хорошо сработать и в других случаях. Пример 15
Получили уравнение относительного исходного интеграла I. Вынося I за скобку, получим
откуда
|
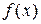 дифференцируема на интервале
дифференцируема на интервале  и
и  для
для  , то эта функция возрастает (убывает) на интервале
, то эта функция возрастает (убывает) на интервале  =
=  , то ее производная в этой точке равна нулю:
, то ее производная в этой точке равна нулю:  .
. -окрестности критической точки х
-окрестности критической точки х  меняет знак с плюса на минус, то х
меняет знак с плюса на минус, то х  , то график выпуклый вниз.
, то график выпуклый вниз. при переходе через точку х
при переходе через точку х  .
. , где
, где ,
,  .
. наклонная асимптота становится горизонтальной и имеет уравнение
наклонная асимптота становится горизонтальной и имеет уравнение 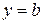 .
. .
. .
.
 , где
, где .
.
 ;
;  ;
; 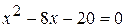 .
. .
.
 )
) )
)







 )
)


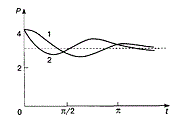
 По результатам исследования построим график функции.
По результатам исследования построим график функции. называется первообразной функции
называется первообразной функции  если
если  Множество первообразных функции
Множество первообразных функции  называется неопределенным интегралом и обозначается
называется неопределенным интегралом и обозначается  .
. ,
, (
(  ), 7)
), 7) 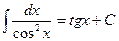 ,
, , 8)
, 8)  ,
, , 9)
, 9)  ,
, , 10)
, 10)  ,
, , 11)
, 11)  ,
, , 12)
, 12)  .
.
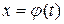 , которая имеет непрерывную производную
, которая имеет непрерывную производную  и обратную функцию
и обратную функцию  . (Например:
. (Например:  монотонна). Тогда справедлива формула:
монотонна). Тогда справедлива формула: . (4.1.1)
. (4.1.1) . (4.1.2)
. (4.1.2) получаем более простой интеграл (4.1.1).
получаем более простой интеграл (4.1.1). .
. .
. .
.
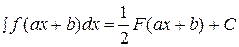 ,
, - первообразная функции
- первообразная функции  .
. .
.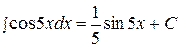 .
.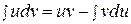 .
.
 - многочлен степени
- многочлен степени  . В качестве
. В качестве  нужно взять
нужно взять  =
= 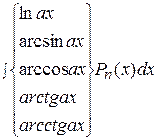 .
. .
. =
=  =
=
 =
=
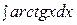 .
.
 .
. по ее дифференциалу
по ее дифференциалу  . Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию.
. Поэтому в качестве этого сомножителя нужно брать легко интегрируемую функцию. .
.


 .
. ,
, .
.