 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Решить однородную систему линейных алгебраических уравнений. Найти фундаментальную систему решений.
Содержание Вариант IX.. 3 1.Выполнить действия над матрицами. 3 2. Вычислить определитель методом понижения порядка до второго. 3 3. Решить неоднородную СЛАУ методом Гаусса или методом Жордана-Гаусса. 4 4. Исследовать на совместность неоднородную систему линейных алгебраических уравнений и решить ее: 5 5. Решить однородную систему линейных алгебраических уравнений. Найти фундаментальную систему решений. 7 6. По координатам точек A, B и C для указанных векторов найти: 8 7. Даны вершины треугольника АВС. Найти: 10 8. Даны четыре точки А, В, С и D. Составить уравнения: 12 9. Построить кривые в полярной системе координат по точкам, придавая 10. Выполнить действия над комплексными числами в алгебраической форме: 15
Вариант IX 1.Выполнить действия над матрицами.
Решение Найдем сумма матриц
Найдем произведение матриц:
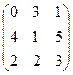
Вычислить определитель методом понижения порядка до второго.
Решение Заданную матрицу разложим по элементам четвертой строки, а матрицы третьего порядка разложим по элементам первой строки:
Ответ: Решить неоднородную СЛАУ методом Гаусса или методом Жордана-Гаусса.
Решение Перепишем систему уравнений в матричном виде и решим его методом Гаусса:
От 2 строки отнимаем 1 строку, умноженную на 2; от 3 строки отнимаем 1 строку, умноженную на 1; к 4 строке добавляем 1 строку, умноженную на 2:
От 3 строки отнимаем 2 строку, умноженную на 2; от 4 строки отнимаем 2 строку, умноженную на 3:
3-ую строку делим на 6:
От 1 строки отнимаем 3 строку, умноженную на 1; к 2 строке добавляем 3 строку, умноженную на 4; от 4 строки отнимаем 3 строку, умноженную на 13:
4-ую строку делим на -0.5:
К 1 строке добавляем 4 строку, умноженную на 0.5; к 3 строке добавляем 4 строку, умноженную на 2.5: Ответ:
4. Исследовать на совместность неоднородную систему линейных алгебраических уравнений и решить ее: 1) матричным методом; 2) по формулам Крамера.
Решение 1) Матричный метод. Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов: Найдем главный определитель: ∆=1·(1·(-1)-2·(-2))-2·(0·(-1)-2·1)+1·(0·(-2)-1·1)=6. Итак, определитель 6 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения. Транспонированная матрица к матрице A имеет вид:
Вычисляем алгебраические дополнения. ∆11=(1·(-1)-(-2·2))=3. ∆12=-(0· (-1)-1·2)=2. ∆13=(0· (-2)-1·1)=-1. ∆21=-(2•(-1)-(-2•1))=0. ∆22=(1· (-1)-1·1)=-2. ∆23=-(1· (-2)-1·2)=4. ∆31=(2·2-1·1)=3. ∆32=-(1·2-0·1)=-2. ∆33=(1·1-0·2)=1. Из полученных алгебраических дополнений составим присоединенную матрицу C:
Вычислим обратную матрицу: Вектор результатов X:
2) По формулам Крамера. Запишем систему в виде: Система совместна тогда и только тогда, когда системный (главный) определитель не равен нулю. Определитель: Заменим 1-ый столбец матрицы А на вектор результата В: Найдем определитель полученной матрицы: ∆1 = -3+0-28+7+12-0=-12.
Заменим 2-ый столбец матрицы А на вектор результата В: Найдем определитель полученной матрицы: ∆2 = 14-6-14+14-14+6=0.
Заменим 3-ый столбец матрицы А на вектор результата В:
Найдем определитель полученной матрицы: ∆3 = -7-0+12-3+28-0=30.
Выпишем отдельно найденные переменные Х: Ответ: Решить однородную систему линейных алгебраических уравнений. Найти фундаментальную систему решений.
Решение
Выпишем основную матрицу системы: Приведем матрицу к треугольному виду. Будем работать только со строками, так как умножение строки матрицы на число, отличное от нуля, и прибавление к другой строке для системы означает умножение уравнения на это же число и сложение с другим уравнением, что не меняет решения системы. Умножим 1-ую строку на (-2). Добавим 2-ую строку к 1-ой: Умножим 2-ую строку на (-1). Умножим 3-ую строку на (2). Добавим 3-ую строку к 2-ой: Умножим 1-ую строку на (-1). Добавим 2-ую строку к 1-ой: В матрице B 1-ая строка нулевая, следовательно, вычеркиваем ее. Это равносильно вычеркиванию 1-го уравнения системы. Найдем ранг матрицы: Выделенный минор имеет наивысший порядок (из возможных миноров) и отличен от нуля (он равен произведению элементов, стоящих на обратной диагонали), следовательно rang(A) = 2. Этот минор является базисным. В него вошли коэффициенты при неизвестных x1,x2, значит, неизвестные x1,x2 – зависимые (базисные), а x3 – свободные. Преобразуем матрицу, оставляя слева только базисный минор6 Система с коэффициентами этой матрицы эквивалентна исходной системе и имеет вид:
Получили соотношения, выражающие зависимые переменные x1,x2 через свободные x3, то есть нашли общее решение. Ответ:
6. По координатам точек A, B и C для указанных векторов найти: а) модуль вектора б) скалярное произведение векторов в) проекцию вектора г) координаты точки
Решение Найдем векторы
Проекцию вектора b на вектор a можно найти по формуле:
Найдем проекцию вектора AB на вектор AB а) Модуль вектора
б) Скалярное произведение векторов
в) проекцию вектора Проекцию вектора
г) Координаты точки Радиус-вектор r точки A, делящий отрезок AB в отношении AA:AB = m1:m2, определяется формулой:
Координаты точки А находятся по формулам:
Ответ: а)
7. Даны вершины треугольника АВС. Найти: а) уравнение стороны AB; б) уравнение высоты CH; в) уравнение медианы AM; г) точку N пересечения медианы AM и высоты CH; д) уравнение прямой, проходящей через вершину С параллельно стороне AB; е) расстояние от точки С до прямой AB. A( -7;3) , B(9;4) , C(5;7) . Решение а) Уравнение стороны AB. Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями: Уравнение прямой AB:
Уравнение прямой BC:
б) Уравнение высоты CH. Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax+By+C=0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями: Найдем уравнение высоты CH:
в) Уравнение медианы AM. Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(-7;3) и М(7;11/2), поэтому: Уравнение прямой:
г) Точку N пересечения медианы AM и высоты CH. Найдем точку пересечения, решив систему уравнений:
Найдем координаты ординаты: Следовательно, имеем
д) Уравнение прямой, проходящей через вершину С параллельно стороне AB. Уравнение прямой AB: Уравнение KЕ параллельно AB находится по формуле: Подставляя x0 = 5,
е) Расстояние от точки С до прямой AB. Расстояние Найдем расстояние между точкой C(5;7) и прямой AB (
Сделаем схематический чертеж:
Ответ: а) д)
8. Даны четыре точки А, В, С и D. Составить уравнения: а) плоскости ABC; б) прямой AB; в) прямой DM, перпендикулярной к плоскости ABC; г) прямой CN, параллельной прямой AB; д) плоскости, проходящей через точку D перпендикулярно к прямой AB. Вычислить: е) синус угла между прямой AD и плоскостью ABC; ж) косинус угла между координатной плоскостью xOy и плоскостью ABC. A(7,5,3) , B(9,4,4) , C(4,5,7) , D(7,9,6) . Решение а) Плоскость ABC. Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением: Уравнение плоскости ABC:
получили
б) Прямая AB. Прямая, проходящая через точки A1(x1; y1; z1) и A2(x2; y2; z2), представляется уравнениями: Уравнение прямой AB: Уравнение прямой AD:
в) Прямая DM, перпендикулярная к плоскости ABC. Направляющим вектором прямой DM будет нормальный вектор плоскости ABC. Составим уравнение прямой по направляющему вектору, проходящей через точку D(7,9,6):
г) Прямая CN, параллельная прямой AB. Направляющим вектором прямой CN будет направляющий вектор прямой AB. Составим уравнение прямой по направляющему вектору, проходящей через точку D(7,9,6):
д) Плоскость, проходящая через точку D перпендикулярно к прямой AB. Уравнение плоскости, проходящей через точку M0(x0, y0, z0) перпендикулярно вектору N = (l,m,n), имеет вид: Координаты точки D(7;9;6). координаты вектора AB(2;-1;1).
Искомое уравнение плоскости:
е) Синус угла между прямой AD и плоскостью ABC. Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле:
Уравнение плоскости ABC: -4x - 11y - 3z + 92 = 0
Уравнение прямой AD:
ж) Косинус угла между координатной плоскостью xOy и плоскостью ABC. Применим формулу:
Ответ: а)
9. Построить кривые в полярной системе координат по точкам, придавая
Решение 1) построим график функции в полярной системе координат по точкам, давая
Построим заданную кривую в полярной системе координат:
Найдем уравнение полученной линии в прямоугольной декартовой системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью: Из условия
Но, так как
Ответ: 10. Выполнить действия над комплексными числами в алгебраической форме:
Решение
Ответ:смотреть выше. |



 значения через промежуток
значения через промежуток  , начиная с
, начиная с  . Найти уравнение полученной линии в прямоугольной системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, привести его к каноническому виду и определить вид кривой. 13
. Найти уравнение полученной линии в прямоугольной системе координат, начало которой совпадает с полюсом, а положительная полуось абсцисс – с полярной осью, привести его к каноническому виду и определить вид кривой. 13 ,
,  . Найти
. Найти  .
. :
:
 Ответ:
Ответ:  .
.

 .
.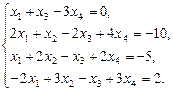






 , откуда получаем решение:
, откуда получаем решение:  .
.
 , вектор B: BT=(3,-14,-7).
, вектор B: BT=(3,-14,-7). .
.
 .
.
 .
. .
. .
. .
.
 .
.
 .
.
 .
. .
. .
. .
. .
. .
.
 .
. - свободная переменная.
- свободная переменная. ;
; ;
; на вектор
на вектор  ;
; , делящей отрезок
, делящей отрезок  в отношении
в отношении 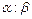 .
. ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  .
. ,
,  ,
,  и
и  .
. ,
,  ,
,  и
и  , следовательно,
, следовательно, ;
; ;
; .
.
 .
. .
. , получим
, получим .
. .
.




 и
и  .
. ; б)
; б)  ; в)
; в)  ; г)
; г) 
 .
.

 .
.
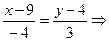
 .
. .
.
 .
. и
и  . Получили
. Получили  .
.

 .
.


 .
. .
. .
. .
. , y0 = 7 получим:
, y0 = 7 получим:  или
или  .
. от точки M1(x1;y1) до прямой
от точки M1(x1;y1) до прямой  равно абсолютному значению величины:
равно абсолютному значению величины:  .
. .
.
 .
. .
. , откуда
, откуда
 .
. .
.
 .
. (нужно будет для пункта е).
(нужно будет для пункта е). .
. .
. .
.
 .
.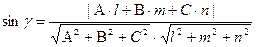
 .
.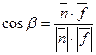 , где
, где  - нормальные векторы плоскостей. Имеем
- нормальные векторы плоскостей. Имеем  и
и  , следовательно
, следовательно .
. ; ж)
; ж)  .
. ;
; значения через промежуток
значения через промежуток 








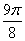









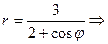
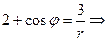
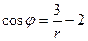 , с другой стороны
, с другой стороны  , отсюда
, отсюда 
 .
.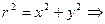
 , следовательно
, следовательно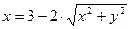


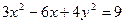
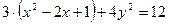

 - получили уравнение эллипса.
- получили уравнение эллипса. ,
, ;
;
 .
.