 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Логарифмическая функция — это функция вида
где a>0, a≠1. 1) Область определения логарифмической функции — множество положительных чисел x>0:
2) Область значений логарифмической функции — множество всех действительных чисел: y∈R
3) Логарифмическая функция не имеет наибольшего и наименьшего значений (не ограничена). 4) Функция не является ни чётной, ни нечётной. 5) Нуль логарифмической функции (y=0): x=1. То есть логарифмическая функция пересекает ось Ox в точке (1;0). Ось Oy не пересекает. 6) При a>1 — логарифмическая функция возрастает на всей области определения. Промежутки знакопостоянства: — функция принимает положительные значения при x>1:
— функция принимает отрицательные значения при 0<x<1:
При 0<a<1 — логарифмическая функция убывает на всей области определения. Промежутки знакопостоянства: — функция принимает положительные значения при 0<x<1:
— функция принимает отрицательные значения при x>1:
7) Для логарифмической функции выполняются соотношения:
Для
График логарифмической функции называют логарифмической кривой. Ось Oy для графика логарифмической функции является вертикальной асимптотой (то есть, при стремлении x к нулю график приближается к оси Oy (но никогда её не пересечёт)).
Логари́фм числа Из определения следует, что нахождение Вычисление логарифма называется логарифмированием. Числа Определение логарифмов и таблицу их значений (для тригонометрических функций) впервые опубликовал в 1614 году шотландский математик Джон Непер. Логарифмические таблицы, расширенные и уточнённые другими математиками, повсеместно использовались для научных и инженерных расчётов более трёх веков, пока не появились электронные калькуляторы и компьютеры. Со временем выяснилось, что логарифмическая функция
Логарифм вещественного числа
Наиболее широкое применение нашли следующие виды логарифмов: · Натуральные: · Десятичные: · Двоичные: Свойства[править | править вики-текст] Основное логарифмическое тождество[править | править вики-текст] Из определения логарифма следует основное логарифмическое тождество[7]:
Следствие: из равенства двух вещественных логарифмов следует равенство логарифмируемых выражений. В самом деле, если Логарифмы единицы и числа, равного основанию[править | править вики-текст] Два равенства, очевидных из определения логарифма:
Логарифм произведения, частного от деления, степени и корня[править | править вики-текст] Приведём сводку формул в предположении, что все значения положительны[8]:
Существует очевидное обобщение приведённых формул на случай, когда допускаются отрицательные значения переменных, например:
Формулы для логарифма произведения без труда обобщаются на произвольное количество сомножителей:
Вышеописанные свойства объясняют, почему применение логарифмов (до изобретения калькуляторов) существенно облегчало вычисления. Например, умножение многозначных чисел 1. найти в таблицах логарифмы чисел 2. сложить эти логарифмы, получая (согласно первому свойству) логарифм произведения 3. по логарифму произведения найти в таблицах само произведение. Деление, которое без помощи логарифмов намного более трудоёмко, чем умножение, выполнялось по тому же алгоритму, лишь с заменой сложения логарифмов на вычитание. Аналогично упрощались возведение в степень и извлечение корня. Замена основания логарифма[править | править вики-текст] Логарифм
Следствие (при
См. пример такой перестановки в разделе десятичный логарифм. Коэффициент Неравенства[править | править вики-текст] Значение логарифма Любое неравенство для положительных чисел можно логарифмировать. При этом, если основание логарифма больше единицы, то знак неравенства сохраняется, а если основание меньше единицы, знак неравенства меняется на противоположный[10]. Другие тождества и свойства[править | править вики-текст] Если выражения для основания логарифма и для логарифмируемого выражения содержат возведение в степень, для упрощения можно применить следующее тождество:
Это тождество сразу получается, если в логарифме слева заменить основание
Ещё одно полезное тождество:
Для его доказательства заметим, что логарифмы левой и правой частей по основанию
|

















 по основанию
по основанию  (от греч. λόγος — «слово», «отношение» и ἀριθμός — «число») определяется[ как показатель степени, в которую надо возвести основание
(от греч. λόγος — «слово», «отношение» и ἀριθμός — «число») определяется[ как показатель степени, в которую надо возвести основание  , произносится: «логарифм
, произносится: «логарифм  равносильно решению уравнения
равносильно решению уравнения  . Например,
. Например,  , потому что
, потому что  .
. чаще всего вещественные, но существует также теория комплексных логарифмов[⇨].Логарифмы обладают уникальными свойствами, которые определили их широкое использование для существенного упрощения трудоёмких вычислений[3]. При переходе «в мир логарифмов» умножение заменяется на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня преобразуются соответственно в умножение и деление на показатель степени. Лаплас говорил, что изобретение логарифмов, «сократив труд астронома, удвоило его жизнь»[4].
чаще всего вещественные, но существует также теория комплексных логарифмов[⇨].Логарифмы обладают уникальными свойствами, которые определили их широкое использование для существенного упрощения трудоёмких вычислений[3]. При переходе «в мир логарифмов» умножение заменяется на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня преобразуются соответственно в умножение и деление на показатель степени. Лаплас говорил, что изобретение логарифмов, «сократив труд астронома, удвоило его жизнь»[4]. незаменима и во многих других областях человеческой деятельности: решениедифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д.. Эта функция относится к числу элементарных, она обратна по отношению к показательной функции. Чаще всего используются вещественные логарифмы с основаниями
незаменима и во многих других областях человеческой деятельности: решениедифференциальных уравнений, классификация значений величин (например, частота и интенсивность звука), аппроксимация различных зависимостей, теория информации, теория вероятностей и т. д.. Эта функция относится к числу элементарных, она обратна по отношению к показательной функции. Чаще всего используются вещественные логарифмы с основаниями  (двоичный),
(двоичный),  (натуральный логарифм) и
(натуральный логарифм) и  (десятичный).
(десятичный). интереса не представляет, поскольку тогда при
интереса не представляет, поскольку тогда при  это уравнение не имеет решения, а при
это уравнение не имеет решения, а при  любое число является решением; в обоих случаях логарифм не определён. Аналогично заключаем, что логарифм не существует при нулевом или отрицательном
любое число является решением; в обоих случаях логарифм не определён. Аналогично заключаем, что логарифм не существует при нулевом или отрицательном  всегда положительно, поэтому следует исключить также случай отрицательного
всегда положительно, поэтому следует исключить также случай отрицательного  имеет смысл при
имеет смысл при 
 (при выполнении указанных условий для
(при выполнении указанных условий для  или
или  , основание: число Эйлера (
, основание: число Эйлера (  или
или  , основание: число
, основание: число  или
или  , основание:
, основание: 
 , то
, то  , откуда, согласно основному тождеству:
, откуда, согласно основному тождеству:  .
.






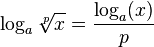

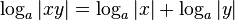
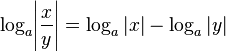


 с помощью логарифмических таблиц[⇨] производилось по следующему алгоритму:
с помощью логарифмических таблиц[⇨] производилось по следующему алгоритму: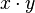 ;
; :
:

 в формуле замены основания называется модулем перехода от одного основания к другому[9].
в формуле замены основания называется модулем перехода от одного основания к другому[9].
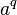 на
на 
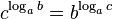
 ), а тогда, согласно следствию из основного логарифмического тождества, левая и правая части тождественно равны.
), а тогда, согласно следствию из основного логарифмического тождества, левая и правая части тождественно равны.