 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Связь между синусом и косинусом одного угла
Определение синуса Определение: Число b, равное ординате единичного радиуса, построенного описанным способом, обозначается sinα и называется синусом угла α. Пример: sin 3π cos3π/2 = 0 0 = 0 Определение косинуса Определение: Число a, равное абсциссе конца единичного радиуса, построенного описанным способом, обозначается cosα и называется косинусом угла α. Пример: cos0 cos3π + cos3,5π = 1 (-1) + 0 = 2 Эти примеры используют определение синуса и косинуса угла через координаты конца единичного радиуса и единичной окружности. Для более наглядного представления необходимо нарисовать единичную окружность и отложить на ней соответствующие точки, а затем посчитать их абсциссы для вычисления косинуса и ординаты для вычисления синуса. Определение тангенса Определение: Функция tgx=sinx/cosx при x≠π/2+πk, kЄZ, называется котангенсом угла x. Область определения функции tgx это все действительные числа, кроме x=π/2+πn, nЄZ. Пример: tg0 tgπ = 0 0 = 0 Этот пример аналогичен предыдущему. Для вычисления тангенса угла нужно поделить ординату точки на её абсциссу. Определение котангенса Определение: Функция ctgx=cosx/sinx при x≠πk, kЄZ называется котангенсом угла x. Область определения функции ctgx = -все действительные числа кроме точек x=πk, kЄZ. Основные тригонометрические тождества представляют собой равенства, устанавливающие связь между синусом, косинусом, тангенсом и котангенсом одного угла, и позволяют находить любую из этих тригонометрических функций через известную другую. Сразу перечислим основные тригонометрические тождества, которые разберем в этой статье. Запишем их в таблицу, а ниже дадим вывод этих формул и приведем необходимые пояснения.
Связь между синусом и косинусом одного угла Иногда говорят не об основных тригонометрических тождествах, перечисленных в таблице выше, а об одном единственном основном тригонометрическом тождестве вида То есть, особый интерес представляет именно равенство Прежде чем доказать основное тригонометрическое тождество, дадим его формулировку: сумма квадратов синуса и косинуса одного угла тождественно равна единице. Теперь докажем его. Обратимся к единичной окружности. Пусть начальная точка A(1, 0) после поворота на угол Равенство Возьмем единичную окружность. Повернем начальную точку A(1, 0) вокруг точки Oна угол
Рассмотрим прямоугольный треугольник OA1H. Хорошо видно, что в нем длины катетов A1H и OH равны соответственно модулю ординаты и абсциссы точки A1, то есть, |A1H|=|y| и |OH|=|x|, а длина гипотенузы OA1 равна радиусу единичной окружности, то есть, |OA1|=1. Теорема Пифагора позволяет записать равенство|A1H|2+|OH|2=|OA1|2, которое мы можем переписать как |y|2+|x|2=12 или y2+x2=1. Но по определению Основное тригонометрическое тождество задает связь между синусом и косинусом одного угла. Это позволяет вычислять синус угла, когда известен косинус этого угла, и вычислять косинус угла, когда известен синус угла. Для этого достаточно равенство Основное тригонометрическое тождество очень часто используется припреобразовании тригонометрических выражений. Оно позволяет сумму квадратов синуса и косинуса одного угла заменять единицей. Не менее часто основное тригонометрическое тождество используется и в обратном порядке: единица заменяется суммой квадратов синуса и косинуса какого-либо угла. Тангенс и котангенс через синус и косинус Тождества, связывающие тангенс и котангенс с синусом и косинусом одного угла вида Благодаря такой очевидности тождеств В заключение этого пункта следует отметить, что тождества Связь между тангенсом и котангенсом Еще более очевидным тригонометрическим тождеством, чем два предыдущих, является тождество, связывающее тангенс и котангенс одного угла вида Доказательство формулы Итак, тангенс и котангенс одного угла, при котором они имеют смысл, есть взаимно обратные числа. Тангенс и косинус, котангенс и синус Наконец, мы пришли к двум последним из основных тригонометрических тождеств Приведем их формулировки: сумма квадрата тангенса угла и единицы равна числу, обратному квадрату косинуса этого угла, а сумма единицы и квадрата котангенса угла равна числу, обратному квадрату синуса этого угла. Вывод указанных формул можно провести, отталкиваясь от основного тригонометрического тождества вида Итак, тождество
|




 . Объяснение этому факту достаточно простое: равенства
. Объяснение этому факту достаточно простое: равенства  получаются из основного тригонометрического тождества после деления обеих его частей на
получаются из основного тригонометрического тождества после деления обеих его частей на 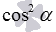 и
и  соответственно, а равенства
соответственно, а равенства  и
и 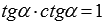 следуют изопределений синуса, косинуса, тангенса и котангенса. Подробнее об этом поговорим в следующих пунктах.
следуют изопределений синуса, косинуса, тангенса и котангенса. Подробнее об этом поговорим в следующих пунктах. переходит в точку A1. В силу определений синуса и косинуса точка A1имеет координаты
переходит в точку A1. В силу определений синуса и косинуса точка A1имеет координаты  . Более того, точка A1 лежит на единичной окружности, следовательно, ее координаты должны удовлетворять уравнению единичной окружности, которое имеет вид x2+y2=1. То есть, должно быть справедливо равенство
. Более того, точка A1 лежит на единичной окружности, следовательно, ее координаты должны удовлетворять уравнению единичной окружности, которое имеет вид x2+y2=1. То есть, должно быть справедливо равенство  . Этим доказано основное тригонометрическое тождество для любых углов поворота
. Этим доказано основное тригонометрическое тождество для любых углов поворота 
 и
и  , тогда от равенства y2+x2=1 мы можем перейти к равенству
, тогда от равенства y2+x2=1 мы можем перейти к равенству  и
и  . Знак перед корнем зависит от величины угла
. Знак перед корнем зависит от величины угла 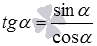 и
и  сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть,
сразу следуют из определений синуса, косинуса, тангенса и котангенса. Действительно, по определению синус есть ордината y, косинус есть абсцисса x, тангенс есть отношение ординаты к абсциссе, то есть,  , а котангенс есть отношение абсциссы к ординате, то есть,
, а котангенс есть отношение абсциссы к ординате, то есть,  .
.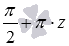 (иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула
(иначе в знаменателе будет нуль, а деление на нуль мы не определяли), а формула  , гдеz - любое целое число.
, гдеz - любое целое число. , в противном случае либо тангенс, либо котангенс не определены.
, в противном случае либо тангенс, либо котангенс не определены. и
и  , откуда
, откуда  . Можно было доказательство провести и немного иначе. Так как
. Можно было доказательство провести и немного иначе. Так как 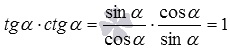 .
. . Если же обе части равенства
. Если же обе части равенства  .
.