 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Контрольные работы, выполненные без учёта указанных правил к рецензированию не принимаются и возвращаются студенту на переработку.
До начала сессии студент может подойти к преподавателю и ознакомиться с замечаниями и рекомендациями, указанными в контрольной работе.
ПРАВИЛА ПРИБЛИЖЕННЫХ ВЫЧИСЛЕНИЙ. При решении физических задач числовые значения, с которыми приходится иметь дело, большей частью являются приближенными. Задачи с приближенными данными следует решать, учитывая правила приближенных вычислений. Правила приближенных вычислений состоят в следующем. 1.Учитывать количество значащих цифр, необходимых для соблюдения определенной точности вычислений. Значащими называют все цифры, кроме нуля, а также нуль в двух случаях: а) когда он стоит между значащими цифрами; б) когда он стоит в конце числа и известно, что единицы соответствующего разряда в данном числе нет. Например: 1603 - 4 значащих цифры; 1,03 - 3 значащих цифры; 1,00 - 3 значащих цифры; 0,00103 - 3 значащих цифры. 2. Так как с помощью вычислений получить результат более точный, чем исходные данные невозможно, то достаточно производить вычисления с числами, содержащими не более знаков, чем в исходных данных. 3. При сложении или вычитании приближенных чисел, имеющих различную точность, более точное должно быть округлено до точности менее точного. Например: 9.6 + 0.176 = 9.6 + 0,2 = 9.8 100,8 - 0,427 = 100,8 -0.4 = 100.4 4. При умножении и делении следует в полученном результате сохранять столько значащих цифр, сколько их имеет приближенное данное с наименьшим количеством значащих цифр. Например: 0.637 × 0.023 = 0.0132 но не 0.0132496; 6.32 : 3 = 2 но не 2.107. 5. При возведении в квадрат или куб нужно сохранять столько значащих цифр, сколько их имеет возводимое в степень число. Например: 1.252 = 1.56, но не 1.5625; 1.013 = 1.03, но не 1.030301 . 6. При извлечении квадратного и кубического корней в результате нужно сохранять столько значащих цифр, сколько их имеет подкоренное число. Например: 101/2 = 3.1, но не 3.162 ; 101/3 = 2.1, но не 2.154. 7. При вычислении сложных выражений соблюдаются правила в зависимости от вида производимых действий. 8. Когда число мало отличается от единицы, можно пользоваться ниже приведенными приближенными формулами. Если a, b , c малы по сравнению с единицей (меньше 0.1), то: (1±a) ×(1±b) ×(1±c) = 1 ± a ± b ± c ; (1±a)1/2 = 1± a/2 ; (1±a)n = 1± n × a; 1/ (1±a)n = 1 + n × a; еа = 1+a; ln(1±a) =±a - a2/2; Если угол меньше 50 и выражен в радианах, то в первом приближении можно принять sin a » tg a » a; cos a » 1. Соблюдая эти правила, студент сэкономит время на вычислениях при решении физических задач. КОНТРОЛЬНАЯ РАБОТА №1 (1 семестр) МЕТОДИЧЕСКИЕ УКАЗАНИЯ Основные законы и формулы механики Скорость мгновенная v = dх/dt Угловая скорость мгновенная w = dj/dt Ускорение : мгновенное а = dv/dt = d2х/dt2 тангенциальное аt = d½v½/dt нормальное аn = v2/r полное a = Ö аt 2 + аt2 Угловое ускорение мгновенное e = dw/dt = d2j/dt2 Cвязь между линейными и угловыми s = jr ; v = wr ; величинами, характеризующими движение аt = e r ; аn = w2 r . точки по окружности . Второй закон Ньютона для поступательного d P/dt = å Fi движения i Второй закон Ньютона для поступательного m a= å Fi движения тела с m =const i Количество движения материальной точки P = mv массы m, движущейся со скоростью v Потенциальная энергия: упругодеформированного тела (работа Епот = А = k х2/2 ; упругой силы) гравитационного взаимодействия двух тел Епот = -G m1m2/r ; тела в однородном поле тяготения Епот = mgh . Кинетическая энергия поступательного Екин = mv2/2 = P2/2m движения тела Момент инерции материальной точки J = mr2 массой m на расстоянии r от оси вращения Моменты инерции некоторых тел массы m относительно оси вращения проходящей через центр тяжести: полого цилиндра (колеса) радиуса R J = m R2 ; сплошного цилиндра (диска) радиуса R J = mR2/2 ; шара радиуса R J = 0.4 mR2 ; стержня длиной ℓ, если ось ^ стержню J = mℓ2/12 ; тела относительно произвольной оси (тео- J = J0 + md2 . рема Штейнера) Момент силы относительно оси вращения М = [ r F ] Момент количества движения L = Jw Основное уравнение динамики вращательного M = d L/dt = d(Jw)/dt движения твердого тела то же для J = const M = J dw/dt = Je Закон сохранения момента количества å Jiwi = const движения Кинетическая энергия вращающегося тела Евращ = Jw2/2 Закон сохранения энергии Епот +Екин +Евращ=const Работа при повороте на угол dj dА = Mdj
Основные законы и формулы молекулярной физики и термодинамики Количество вещества n = N/NA = m/m Уравнение Клапейрона - Менделеева (уравнение РV = mRT/m состояния идеального газа ) Закон Дальтона Р = P1 + P2 +....+ Pn Концентрация молекул n = N/V = NAr/m Закон Фурье q =-l (dT/dх) Первое начало термодинамики dQ = dU + dA Отношение температур и объемов газа, совершающего адиабатический процесс, Работа газа при изотермическом процессе
Внутренняя энергия произвольной массы газа U = m∙i∙RT/(2∙μ) Работа газа при изобарном расширении A = m∙R(T2-T1)/μ
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ Пример 1. Маховик в виде колеса массой m = 30 кг и диаметром 60 см вращается с угловой скоростью w, изменяющейся по закону w = Аt10 , где А = 2 рад/с11. Найти закон движения j(t), угловое ускорение e (t), момент сил М(t) и момент количества движения L(t). Вычислить эти величины через 2 с после начала движения. Считать начальный угол j(t =0) = j0 = 0 . Решение. Перевод в СИ m = 30 кг 30 кг D = 60 см 0,6 м w = Аt10 = 2× t10рад/с11 2× t10рад/с t = 2 c 2 c Определить: j(t), e (t), М(t), L(t). Если известен закон движения, то угловая скорость определяется как первая производная от j(t) по времени: dj w(t) = ¾¾ (1) dt Закон движения j(t) находится решением обратной задачи, т.е. интегрированием угловой скорости по времени:
j(t) =
При w(t) = 2 ×t10 ,с учетом j0 = 0: j(t) = В момент времени t = 2 с маховик повернулся на угол j(t =2 с) = Угловое ускорение определяется как первая производная от угловой скорости по времени:
dw d e = ¾¾ = ¾¾ ( 2 ×t10) = 10 × 2× t9 (4) dt dt В момент времени t = 2 c угловое ускорение равно: e ( t = 2c) = 10 × 2 × 29 = 10240 » 1,02× 104 рад/с2 Момент сил можно определить из основного закона динамики для вращательного движения твердого тела: М = I × e (5) где I - момент инерции тела. В нашем случае момент инерции колеса равен: I = mR2 = mD2/4 (6)
Подставляя выражения (4) и (6) в (5) получим: mD2 20 t9 М = ¾¾ ×¾¾ При t = 2 c 30 × ( 0,6)2 20×29 M = ¾¾ ¾¾ ¾¾ ¾¾ = 27648 » 2,77 × 104 Н×м Момент количества движения равен: L = I w (7) Подставляя выражения для w и (6) в (7) получим: mD2 2 t10 L = ¾¾ ¾¾ При t = 2 c 30× (0,6)2 × 2× 210 L = ¾¾ ¾¾ ¾¾ = 5529,6 = 5,53× 103 кг м2/с Проверим размерность полученных выражений. рад с11 [j] = [А] [t11] = ¾¾¾¾ = рад; с11
рад с9 [e] = [А] [t9] = ¾¾¾¾ = рад/с2 с11
mD2 × A t9 кг м2 с9 кг м м [M] = [¾¾¾¾¾¾¾¾ ] = ¾¾¾¾ = ¾¾¾¾ = Н м 4 11 с11 с2 кг м2 c10 [L] = [ m D2 A t10 ] = ¾¾¾¾ = кг м2 с-1 c11 Ответ: j(t=2) =372рад, e(t=2с)= 1,02× 104 рад/с2, М(t) =2,77 × 104 Н м L(t) = 5,53× 103 кг м2/с
Пример 2. Соковыжималка раскручивается до 7200 об/мин. Определить силу, действующую на кусочек яблока массой 5г, при диаметре камеры D = 24 см. Вычислить линейную скорость кусочка яблока. Оценить мощность соковыжималки, если максимальные обороты достигаются за 8с. Барабан представляет собой полуцилиндр, масса дна и кольца примерно одинакова и равна 100 г. Яблочная масса при загрузке составляет 300 г. Решение. СИ n = 7200 об/мин = 120 с-1 R = D/2 = 12 см = 0,12 м m = 5 г = 5 ·10-3 кг m1 = 100 г = 0,1 кг m2 = 300 г = 0,3 кг t = 8с Определить: силу F, скорость V, мощность Р Кусок яблока движется по круговой траектории с центростремительным ускорением а = V2/ R . (1) Сила, действующую на кусочек яблока со стороны барабана, равна F= mV2/ R . С силой F кусок яблока прижимается к барабану. Поэтому искомая сила равна F= mV2/ R = F= mw2 R , (2) где V = w R –линейная скорость кусочка яблока; w = 2π n - угловая скорость Проверим размерность подставляя: кг· с-2 · м [F] = [¾¾¾¾¾] = кг· м·с-2 = Н Проведем вычисления: Сила F = mw2 R= 5 ·10-3 ·(2 ·3,14)2 ·(120)2×0,12=5·10-3 ·4·9,86·1,44·104 ×0,12=2,84·103 Н Линейная скорость кусочка яблока: V = w R = 2π n R =2·3,14 ·120 · 0,12 =30.432 ≈ 30.4 м/с Мощность соковыжималки можно оценить, вычислив кинетическую энергию вращающегося барабана вместе с содержимым и разделив её на время раскручивания . Кинетическая энергия вращения равна: Екин = (I + I1) w2 /2 где I = m2 R 2 – момент инерции яблочной массы; I1 = m1 R 2 / 2 + m1 R 2 момент инерции полуцилиндра, состоящего из диска и кольца. I = 0,3· (0,25)2 = 0.0185 =1.875·10-2 кг·м2 ≈ 1.88·10-2 кг·м2 I1 =(0.05 +0.1) · (0,25)2 = 0.93675·10-2 кг·м2≈ 0.937·10-2 кг·м2 Екин= (1.88 + 0.937) ·10-2 ·(2π 120)2 / 2 = 2.82 ·10-2 · 2· (3,14)2 1.44· 104 ≈ 8.01·103 Дж. Мощность соковыжималки: Р = Екин / t =8.01·103 / 8 ≈ 103 Вт Размерность полученных результатов проверяем аналогичным способом, описанным в примерах 1 и 2. Ответ: сила, прижимающая кусочек яблока к барабану F = 2,84·103 Н, линейная скорость кусочка яблока:V ≈ 30.4 м/с ; мощность соковыжималки Р ≈ 103 Вт.
Пример 3. Автомобиль тянет платформу с грузом, представляющим собой прямоугольную форму весом 250 кг. Коэффициент трения между платформой и грузом 0,05, вес платформы 820 кг. Сила с которой тянет автомобиль платформу изменяется по закону F=Аt, где А=4,25[кг×м/с3] – некоторая постоянная. Определить: 1) момент времени t0, когда платформа начнет выскальзывать из-под груза; 2) ускорения груза а1 и платформы а2 в процессе движения. Решение. m1=250 кг Описанный процесс схематично изображен на рис.1. m2=820 кг Сила, с которой машина тянет платформу, можно выразить f=0,05 формулой F=Fтр+m2a2 (1), где Fтр= m1a1 (2). Максимальное F=4,25t значение силы трения равно Fтр.max= f m1 g (3), ______________ Найти t0=? где g=9,81 м/с2 - есть ускорение свободного падения. а1=? Используя выражения (1), (2) и (3), определим ускорение а2 и, а2=? подставим его в очевидное неравенство, а2 ³ а1, показывающее
Рис. 1. предельное значение ускорения, при котором груз уже скользит по платформе.
а2 = Во время t=t0
Во время t£t0 а1=а2= Во время t£t0 а1=fg=const, а2= Так как исходные данные приведены в системе единиц СИ, то подставим в полученные выражения числовые значения и рассчитаем требуемые неизвестные. t0=
а1=9,81×0,05=0,49 м/с2.
а2= Размерность полученных результатов проверяем аналогичным способом, описанным в примерах 1 и 2.
Ответ: 1) время, после начала движения при котором платформа начнет выскальзывать из под груза больше t0= 123,49 с; 2) ускорение груза достигнет а1= 0,49 м/с2; 3) платформа должна двигаться с ускорением больше, чем а2= 0,49 м/с2.
Пример 4. С башни, высотой 20 м, горизонтально со скоростью 10 м/с из пращи брошен камень массой 400 г. Пренебрегая сопротивлением воздуха определить для момента времени 1с после начала движения кинетическую и потенциальную энергии. Решение. H= 20 м Запишем формулы для расчета кинетической и потенциа- u0= 10 м/с льной энергий: m= 400 г = 0,4 кг Т = t= 1 с ______________ Найти: В формулах не все данные известны. Необходимо найти Т = ?; П = ?. общую скорость движения камня через 1 с и высоту на которой камень будет находиться через это время. Скорость движения при снижении камня по вертикали определяется выражением uy = g×t, а полная скорость движения u2 = u02 + uy2, где u0 = const – постоянная скорость движения камня по горизонтали, uy – скорость равнопеременного движения камня по вертикали. Подставив полученные формулы в выражение для кинетической энергии, окончательно получим: Т = m ×(u02+g2 × t2) / 2. За время t камень опустится на высоту h1 = П = m×g×(H - Проведем вычисления: Т = m ×(u02+g2 × t2) / 2 = 0,4×(102 + 9,812×12) / 2 = 39,2 Дж; П = m×g×(H - Ответ: 1) кинетическая энергия камня через секунду после начала движения равна Т = 39,2 Дж; 2) потенциальная энергия равна П = 59,2 Дж. Размерность полученных результатов проверяем аналогичным способом, описанным в примерах 1 и 2.
Пример 5. В цилиндре под поршнем находится водород массой 20 г, при температуре 250С. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти температуру в конце адиабатического процесса расширения и работу, совершенную газом. Изобразить процесс графически. Решение. СИ М = 20г 0.02 кг T1 = 250C Т1 = 298 К V1а/ V2а = 5 V2и/ V1и = 1/5 R = 8,31 Дж/моль∙град µ=2 ∙10-3 кг/моль i = 5 γ = 1,4 ________________________________ Определить: Т2=?; А1=?; А2=?.
Отношение температур и объемов газа, совершающего адиабатический процесс, описываются равенством:
где γ – отношение теплоемкостей газа при постоянном давлении и постоянном объеме. Отсюда получаем выражение для конечной температуры Т2:
Подставляя численные значения, получаем: Т2 = 298∙(1/5)1,4-1 = 298∙0.525 = 156,5 К. Работа газа при адиабатическом расширении определим по формуле:
Подставляя цифровые значения в полученное выражение, получаем:
Работа газа при изотермическом процессе может быть выражена формулой:
Подставляя известные числовые значения, величин входящих в формулу, и выполняя арифметические операции, находим работу при изотермическом процессе:
Знак «минус» показывает, что при сжатии газа работа совершается над газом внешними силами. График описанного процесса представлен на рис.1.
Рис. 1. Ответ: Температура в конце адиабатического процесса расширения Т2 = 156,5 К. Работа, совершенная газом для точек 2,3 равна А1=8,62∙104Дж, А2=-2,08∙104Дж.
Пример 6. Определить плотность смеси газов (60 % пропана - С3Н8,30%, бутана - С4 Н10 и 10% метана - CH4) находящихся в баллоне при температуре 27 0С и давлении 0.11МПа. Решение. СИ m1(С3Н8) = (3×12 +8×1) × 10-3 = 44×10-3кг/моль m1/m= 0.6 - “ - m2 (С4H10) = (4×12 + 10×1) ×10-3=56×10-3 кг/моль m2/m =0.3 - “ - m3 (СН4) = ( 12 + 4×1) ×10-3 = 16×10-3 кг/моль m3/m = 0.1 - “ - t = 270C Т = 300 К P = 0.11 MПа 0.11× 106 Па ____________________________________ Определить: r = ? По закону Дальтона давление смеси газов P равно сумме парциальных давлений газов, составляющих смесь P1( C3 H8), P2(C4 H10) ,P3 (CH4) : P = P1 + P2 + P3 (1) Для каждого газа справедливо уравнение состояния (Клапейрона -Менделеева): Pi V = (mi /mi )RT (2) Из выражения (2) можно выразить парциальное давление: Pi = (mi /mi )RT/V (3) Уравнение Клапейрона - Менделеева справедливо и для смеси газов: P V = (m /m)RT (4) Плотность газа равна: r = m/V = Pm/ RT (5) Молярную массу смеси можно найти подставив (3) в (1): P = (m1/m1)RT/V + (m2 /m2 )RT/V + (m3 /m3 )RT/V = (m/m) RT/V (6) Из уравнения (6) молярная масса m равна: m = (m1/m1m + m2/m2m + m3/m3m)-1 (7) Подставляя (7) в (5) получим выражение для плотности смеси: r = P/ RT (m1/m1m + m2/m2m + m3/m3m) Проверим размерность получившейся формулы: [r]=[P] /[R][T] [m-1]=Па/ (Дж моль-1К-1) К (кг/моль)-1=Па/Дж кг-1=Нм-2 кг/Нм= кг/м3 r = 0.11×106 /8.31 300 (0.6/44×10-3 + 0.3/ 56×10-3 + 0.11/6×10-3) = (0.11× 39.6 /8.31×3×) × 106-2-3 = 0.175×10 =1.75 кг/м3 Ответ: плотность смеси газов r = 1.75 кг/м3.
ЗАДАНИЯ К КОНТРОЛЬНОЙ №1 10. Маховик в виде сплошного диска массой 20 кг и диаметром 20 см вращается в соответствии с законом движения j(t) . Определить угловую скорость, угловое ускорение, момент сил, действующий на маховик, и момент количества движения маховика в момент времени t = 2с. Закон движения в соответствии с номером задачи дан в табл. 1. Таблица 1
11. Соковыжималка фирмы Brown раскручивается до 1000 об/мин. Определить силу , действующую на кусочек яблока массой 10 г, при диаметре камеры D =18 см. Вычислить линейную скорость кусочка яблока. Оценить мощность соковыжималки, если максимальные обороты достигаются за 10с. Барабан представляет собой полуцилиндр, масса дна и кольца примерно одинакова и равна 100 г. Яблочная масса при загрузке составляет 300 г. 12. Отечественная соковыжималка раскручивается до 1200 об/мин. Определить силу, действующую на кусочек яблока массой 10 г, при диаметре камеры D =24 см. Вычислить линейную скорость кусочка яблока. Оценить мощность соковыжималки, если максимальные обороты достигаются за 10с. Барабан представляет собой полуцилиндр, масса дна и кольца примерно одинакова и равна 100 г. Яблочная масса при загрузке составляет 300 г. 13. Стиральная машина фирмы Ariston в режиме отжима достигает 1000 об/мин при диаметре барабана 50см. Определить силу, прижимающую кусочек ткани массой 100 г к барабану. Вычислить линейную скорость капли воды на ободе барабана. Оценить мощность стиральной машины , если максимальные обороты достигаются за 2с. Барабан представляет собой полуцилиндр, масса дна и кольца примерно одинакова и равна 1,5 кг. Масса белья при загрузке составляет 5кг. 14. Стиральная машина фирмы Candy в режиме отжима достигает 600 об/мин при диаметре барабана 50см. Определить силу, прижимающую кусочек ткани массой 100 г к барабану. Вычислить линейную скорость капли воды на ободе барабана. Оценить мощность стиральной машины, если максимальные обороты достигаются за 2с. Барабан представляет собой полуцилиндр, масса дна и кольца примерно одинакова и равна 1,5 кг. Масса белья при загрузке составляет 4кг. 15. Стиральная машина фирмы LG в режиме отжима достигает 900 об/мин при диаметре барабана 60см. Определить силу, прижимающую кусочек ткани массой 100 г к барабану. Вычислить линейную скорость капли воды на ободе барабана. Оценить мощность стиральной машины, если максимальные обороты достигаются за 2с. Барабан представляет собой полуцилиндр, масса дна и кольца примерно одинакова и равна 2,0 кг. Масса белья при загрузке составляет 5кг. 16 Стиральная машина фирмы Ariston в режиме отжима достигает 700 об/мин при диаметре барабана 50см. Определить силу, прижимающую кусочек ткани массой 100 г к барабану. Вычислить линейную скорость капли воды на ободе барабана. Оценить мощность стиральной машины, если максимальные обороты достигаются за 4с. Барабан представляет собой полуцилиндр, масса дна и кольца примерно одинакова и равна 1,5 кг. Масса белья при загрузке составляет 5кг. 17. Горизонтальная центрифуга развивает 500 об/мин. Определить силу, действующую на тело массой 1г, если диаметр центрифуги 20 см. Вычислить линейную скорость на ободе барабана центрифуги. 18. Горизонтальная центрифуга развивает 600 об/мин. Определить силу, действующую на тело массой 1г, если диаметр центрифуги 20 см. Вычислить линейную скорость на ободе барабана центрифуги. 19. Горизонтальная центрифуга развивает 1200 об/мин. Определить силу, действующую на тело массой 1г, если диаметр центрифуги 20 см. Вычислить линейную скорость на ободе барабана центрифуги. 20. Горизонтальная центрифуга развивает 750 об/мин. Определить силу, действующую на тело массой 1г, если диаметр центрифуги 20 см. Вычислить линейную скорость на ободе барабана центрифуги. 21. Рабочие лебедкой поднимают груз массой 50 килограмм по наклонной плоскости с углом наклона 300 к горизонту на расстояние 4 м. Время подъема 8 с, а коэффициент трения 0,06. Определить работу, совершаемую при подъеме груза. 22. Рабочие лебедкой поднимают груз массой 150 килограмм по наклонной плоскости с углом наклона 450 к горизонту на расстояние 4,2 м. Время подъема 18 с, а коэффициент трения 0,09. Определить работу, совершаемую при подъеме груза. 23. Автомобиль тянет платформу с грузом, представляющим собой прямоугольную форму весом 450 кг. Коэффициент трения между платформой и грузом 0,02, вес платформы 740 кг. Сила с которой тянет автомобиль платформу изменяется по закону F=Аt, где А= 4,25[кг×м/с3] – некоторая постоянная. Определить: 1) момент времени t0, когда платформа начнет выскальзывать из-под груза; 2) ускорения груза а1 и платформы а2 в процессе движения. 24. Тягач тянет платформу с грузом, представляющим собой прямоугольную форму весом 600 кг. Коэффициент трения между платформой и грузом 0,07, вес платформы 1300 кг. Сила с которой тянет тягач платформу изменяется по закону F=Аt, где А=6,42[кг×м/с3] – некоторая постоянная. Определить: 1) момент времени t0, когда платформа начнет выскальзывать из-под груза; 2) ускорения груза а1 и платформы а2 в процессе движения. 25. Автокар тянет платформу с грузом, представляющим собой прямоугольную форму весом 110 кг. Коэффициент трения между платформой и грузом 0,03, вес платформы 80 кг. Сила с которой тянет автокар платформу изменяется по закону F=Аt, где А=3,5[кг×м/с3] – некоторая постоянная. Определить: 1) момент времени t0, когда платформа начнет выскальзывать из-под груза; 2) ускорения груза а1 и платформы а2 в процессе движения. 26. Автомобиль тянет платформу с грузом, представляющим собой прямоугольную форму весом 200 кг. Коэффициент трения между платформой и грузом 0,08, вес платформы 710 кг. Сила с которой тянет автомобиль платформу изменяется по закону F=Аt, где А= 2,8[кг×м/с3] – некоторая постоянная. Определить: 1) момент времени t0, когда платформа начнет выскальзывать из-под груза; 2) ускорения груза а1 и платформы а2 в процессе движения. 27. Тягач тянет платформу с грузом, представляющим собой прямоугольную форму весом 940 кг. Коэффициент трения между платформой и грузом 0,04, вес платформы 1500 кг. Сила с которой тянет тягач платформу изменяется по закону F=Аt, где А=7,3[кг×м/с3] – некоторая постоянная. Определить: 1) момент времени t0, когда платформа начнет выскальзывать из-под груза; 2) ускорения груза а1 и платформы а2 в процессе движения. 28. Автокар тянет платформу с грузом, представляющим собой прямоугольную форму весом 50 кг. Коэффициент трения между платформой и грузом 0,02, вес платформы 90 кг. Сила с которой тянет автокар платформу изменяется по закону F=Аt, где А=2,55[кг×м/с3] – некоторая постоянная. Определить: 1) момент времени t0, когда платформа начнет выскальзывать из-под груза; 2) ускорения груза а1 и платформы а2 в процессе движения. 29. Поезд массой 600 т движется под гору с уклоном 0,30 и за время 1 мин развивает скорость 18 км/час. Коэффициент трения 0,01. Определить среднюю мощность локомотива и совершаемую им работу на этом участке пути. 30. Электричка массой 5200 т движется в гору с уклоном 0,20 с постоянной скоростью 40 км/час. Время движения 10 мин. Коэффициент трения 0,012. Определить среднюю мощность электрички и совершаемую работу на этом участке пути. 31. Тело брошено вертикально вверх со скоростью 20 м/с. Пренебрегая сопротивлением воздуха, определить, на какой высоте кинетическая энергия тела будет равна его потенциальной энергии. Ускорение свободного падения принять равным 9,81 м/с2. 32. Тело массой 0,5 килограмм брошено со скоростью 10 м/с под углом 300 к горизонту. Пренебрегая сопротивлением воздуха определить кинетическую и потенциальную энергии тела через 0,4 с после начала движения. 33. Тело массой 1,5 килограмм брошено со скоростью 8 м/с под углом 450 к горизонту. Пренебрегая сопротивлением воздуха определить кинетическую и потенциальную энергии тела через 0,2 с после начала движения. 34. Спортсмен бросает ядро массой 5 килограмм под углом 600 к горизонту, совершая при этом работу 500 Дж. Пренебрегая сопротивлением воздуха определить, через какое время ядро упадет на землю. 35. Спортсмен бросает ядро массой 5 килограмм под углом 450 к горизонту, совершая при этом работу 500 Дж. Пренебрегая сопротивлением воздуха, определить какое расстояние пролетит ядро до соприкосновения с землей. 36. Спортсмен бросает ядро массой 5 килограмм под углом 600 к горизонту. Ядро пролетает расстояние 17,6 м за время 2,5 с. Пренебрегая сопротивлением воздуха определить работу, совершенную спортсменом при бросании ядра. 37. Тело брошено под углом 450 к горизонту со скоростью 15 м/с. Используя закон сохранения энергии определить скорость в высшей точке его траектории. 38. Самолет, летевший на высоте 2940 м со скоростью 360 км/ч, сбросил бомбу. За какое время до прохождения над целью и на каком расстоянии от нее самолет должен сбросить бомбу, чтобы попасть в цель (сопротивлением воздуха пренебречь). 39. Тело брошено под углом 300 к горизонту со скоростью 12 м/с. Используя закон сохранения энергии определить скорость в высшей точке его траектории. 40. Самолет, летевший на высоте 3500 м со скоростью 400 км/ч, сбросил бомбу. За какое время до прохождения над целью и на каком расстоянии от нее самолет должен сбросить бомбу, чтобы попасть в цель (сопротивлением воздуха пренебречь). 41. Работа расширения некоторого двухатомного идеального газа составляет 2 кДж. Определить количество подведенной к газу теплоты, если процесс протекал изотермически. Процесс изобразить графически. 42. Работа расширения некоторого двухатомного идеального газа составляет 2,2 кДж. Определить количество подведенной к газу теплоты, если процесс протекал изобарно. Процесс изобразить графически. 43. При адиабатном расширении кислорода (ν = 2 моль), находящегося при нормальных условиях, его объем увеличился в 3 раза. Определить работу расширения газа и изменение его внутренней энергии. Процесс изобразить графически. 44. Азот массой 1000 грамм занимает при температуре 270С объем 0,5 м3. В результате адиабатного сжатия давление газа увеличилось в 3 раза. Определить: конечный объем, конечную температуру и изменение внутренней энергии газа. Процесс изобразить графически. 45. Азот, находящийся при температуре 1270С, подвергли адиабатному расширению, в результате которого объем его увеличился в 5 раз, а внутренняя энергия уменьшилась на 4 кДж. Определить массу азота. Процесс изобразить графически. 46. Кислород массой 10 г, находящийся при температуре 970С, подвергли адиабатному расширению, в результате которого его давление уменьшилось в 4 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления. Определить количество теплоты, отданное газом, работу, совершенную газом. Процесс изобразить графически. 47. Кислород массой 12 г, находящийся при температуре 900С, подвергли адиабатному расширению, в результате которого его давление уменьшилось в 3 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления. Определить количество теплоты, отданное газом, работу, совершенную газом. Процесс изобразить графически. 48. Кислород массой 10 г, находящийся при температуре 900С, подвергли адиабатному расширению, в результате которого его давление уменьшилось в 4 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления. Определить количество теплоты, отданное газом, работу, совершенную газом. Процесс изобразить графически. 49. Кислород массой 12 г, находящийся при температуре 800С, подвергли адиабатному расширению, в результате которого его давление уменьшилось в 3 раза. В результате последующего изотермического процесса газ сжимается до первоначального давления. Определить количество теплоты, отданное газом, работу, совершенную газом. Процесс изобразить графически. 50. Азот, находящийся при температуре 700С, подвергли адиабатному расширению, в результате которого объем его увеличился в 3 раз, а внутренняя энергия уменьшилась на 1,2 кДж. Определить массу азота. Процесс изобразить графически. 51. Определить плотность смеси газов (50 % пропана - С3Н8,40% бутана - С4 Н10 и 10% метана - CH4) находящихся при температуре 7 0С и давлении 0.11МПа. 52. .Природный газ содержит 80% метана (СН4), 18 % пропана(С3Н8), 2% бензола (С6Н6). Определить массу газа в баллоне объемом 50 л при температуре 70С и давлении 1Мпа 53. В сосуде находится 100 г газа при температуре 170С. После дополнительной подкачки газа в сосуд давление увеличилось на 60 %, а температура повысилась на 300С. Найти массу газа введенного в сосуд. 54. В баллоне емкостью 40 л находится 4 кг водорода и 6.5 кг азота. Определить давление смеси, если температура окружающей среды 170С. 55. Определить плотность воздуха (78% азота - N2 , 21% кислорода O2 , 1% CO2) при температуре 270С и давлении 0.11 МПа. 56. В сосуде емкостью 30 л находится 1 г водорода и 12 г гелия. Определить температуру газа, если давление внутри сосуда 400 кПа 57. Определить массу газа, находящегося в баллоне емкостью 25 л при температуре - 230С и давлении 200 кПа. Плотность газа при нормальных условиях 2 кг/м3. 58. Природный газ содержит 90% метана (СН4) , 8% - азота (N2) и 2 % бензола (C6 H6). Определить массу газа в баллоне объемом 50 л при давлении 1МПа и температуре окружающего воздуха 70С. 59. Определить плотность смеси газов (60 % пропана - С3Н8,20% бутана - С4 Н10 и 20% метана - CH4) находящихся при температуре 17 0С и давлении 0.11МПа. 60. В сосуде, имеющим форму шара, радиус которого 0.2 м находится 80 г азота. До какой температуры можно нагреть сосуд, если его стенки выдерживают давление 7· 105 Па? |



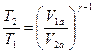
 .
.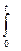 w(t) d t + j0 (2)
w(t) d t + j0 (2) (3)
(3) = 372,3 » 372 рад.
= 372,3 » 372 рад.
 ; а1=fg; тогда
; а1=fg; тогда  .
. , из чего выразим t0=
, из чего выразим t0=  .
.
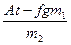 .
.
 .
. ; П = m×g×h.
; П = m×g×h. , тогда потенциальная энергия камня будет равна
, тогда потенциальная энергия камня будет равна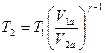 .
.
 .
. .
.