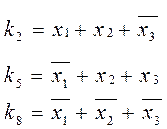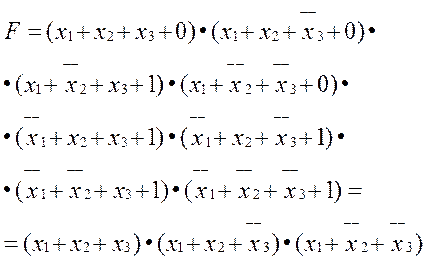ПОЗНАВАТЕЛЬНОЕ

Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.

Отёска стен и прирубка косяков - Когда на доме не достаёт окон и дверей, красивое высокое крыльцо ещё только в воображении, приходится подниматься с улицы в дом по трапу.

Дифференциальные уравнения второго порядка (модель рынка с прогнозируемыми ценами) - В простых моделях рынка спрос и предложение обычно полагают зависящими только от текущей цены на товар.

ЛОГИЧЕСКИЕ ФУНКЦИИ И АЛГЕБРА ЛОГИКИ (БУЛЕВА АЛГЕБРА)

12 3

Логические функции и способы их записи

В устройствах цифровой электроники используются элементы, входные и выходные сигналы которых могут принимать лишь два значения: логической единицы «1» и логического нуля «О». Такие элементы, называемые логическими, осуществляют простейшие операции с такими двоичными числами.

Для описания алгоритмов работы и структуры логических схем используют простую алгебру логики, или булеву алгебру, называемую по имени разработавшего ее в середине XIX века ирландского математика Д. Буля. В ее основе лежат три основные логические операции: логическое отрицание, или операция НЕ (инверсия), логическое сложение, или операция ИЛИ (дизъюнкция) и логическое умножение, или операция И (конъюнкция).

Операция НЕ над переменной х записывается в виде .

Операция ИЛИ над двумя переменными х и у записывается в виде х + у, а операция И — в виде х • у.

Фактически каждая логическая операция задает функцию своих аргументов (переменных). Поэтому можно говорить о функциях дизъюнкции, конъюнкции и инверсии.

Число аргументов функций дизъюнкции и конъюнкции может быть произвольным (больше двух).

Некоторая логическая функция может быть задана в алгебраической форме или в виде таблицы истинности.

Алгебраическая форма, или булево выражение представляет собой формулу, состоящую из логических переменных, связанными операциями И, ИЛИ и НЕ, например:

f(x₁, x₂, x₃)= x_1* x_2* x₃+( x₁₊ x₂) _* (x_1*x₃).

Как и в обычных алгебраических выражениях для задания порядка действий используются скобки. Предполагается, что выполнение операции И предшествует операции ИЛИ.

Таблицей истинности называется таблица, содержащая все возможные комбинации значений входных переменных и соответствующие им значения логической функции. Taк, для логической функции n переменных таблица истинности содержит 2ⁿ строк и n + 1 столбцов, как показано в таблице на рис. 1.

Х₁	Х₂	-	Х_n	f(x₁,x₂,..,x_n)
0		-		f(0,0,...,0₎
		-		f(0,0,...,1₎
		-		f(1,1,...,1₎

Рис. 1

Очевидно, что значение логической функции f(x₁,x₂,..,x_n₎в каждой строке будет принимать значение 0 или 1 в зависимости от значений входных логических переменных.

Поскольку булево выражение и соответствующая ей таблица истинности описывают одну и ту же функцию, то можно переходить от одной формы описания к другой.

Таблицы истинности логический функций И, ИЛИ, НЕ приведены на Рис.2.

Функция И Функция ИЛИ Функция HE

x	y	f(x,y)

x	y	f(x,y)

x	f(x)

Рис. 2

Построим таблицу истинности (Рис. 3) для выше приведенного булева выражения

f(x₁, x₂, x₃)= x_1* x_2* x₃+( x₁₊ x₂) _* (x_1*x₃).

X₁	X₂	X₃	f(x₁,x₂,x₃)

Рис. 3

Чтобы построить таблицу, нужно вычислить значение функции f(x₁,x₂,x₃) для каждой из восьми комбинаций значений входных переменных.

Tак, например, при х₁=0. х₂ = 0. х₃=0. получим

f(0,0,0) = 0•0•0+(0+0)•(0+0)=0+0•(0+1)=0+0=0

Для x₁=1,x₂=1,x₃=1, получим

f(1,1,1)=1•1•1+(1+1)•(1+1)=1+1•(1+0)=1+1•1=1+1=1.

По таблице истинности также можно составить алгебраическое (булево) выражение. При этом запись алгебраического выражения осуществляется с использованием совершенной дизъюнктивной нормальной формы (СДНФ) или совершенной конъюнктивной нормальной формы (СКНФ).

Для представления логической функции F в виде СДНФ необходимо составить сумму (дизъюнкцию) произведений (конъюнкций) значений логической функции F_i и минтермов m_i причем число слагаемых n равно числу строк в таблице истинности, т. е.

Минтерм m_i —это логическое произведение всех переменных, причем переменные, равные нулю, записываются с инверсией.

Так для таблицы истинности (см. Рис. 3) можно записать следующие миитермы:

Следовательно, логическая функция F, заданная таблицей истинности, имеет следующую СДНФ:

F=m₁•0+m₂•0+m₃•1+m₄•0+m₅•1+m₆•1+m₇•1+m₈•1=

=x_1• x_2• x₃₊ x_1• x_2• x₃₊ x_1• x_2• x₃₊ x_1• x_2• x₃₊ x_1• x_2• x₃

Таким образом, для записи функции в виде СДНФ можно использовать следующее правило: следует записать столько дизъюнктивных членов, представляющих собой конъюнкции (произведения) всех переменных, сколько раз функция принимает значение 1, причем переменные, равные нулю, записываются с инверсией.

Для представления логической функции F в виде СКНФ необходимо составить произведение (конъюнкцию) сумм (дизъюнкций) значений логической функции F_i и макстермов k_i, причем число произведений n равно числу строк в таблице истинности, т. е.

Макстeрм k_i— это логическая сумма всех переменных, причем переменные, равные 1, записываются с инверсией.

Так, для таблицы (см. Рис. 3) можно записать следующие макcтермы:

Следовательно, логическая функция F, заданная таблицей истинности, описывается следующей СКИФ:

Таким образом, для записи функции в виде СКНФ используют следующее правило: следует записать столько конъюнктивных членов, представляющих собой дизъюнкции (суммы) всех переменных, сколько раз функция принимает значение 0, причем переменные, равные единице, записываются с инверсией.

Основы алгебры логики

Рис. 4

Наиболее важные теоремы, отражающие основные соотношения алгебры логики, приведены в таблице (Рис. 4).

Легко заметить, что все теоремы (кроме 5) представлены парой соотношений, каждое из которых получается заменой операций И на ИЛИ, операции ИЛИ на И, логической 1 на логический 0 и логического 0 на логическую 1. Теоремам булевой алгебры присуще свойство симметрии, известное как принцип двойственности.

Правильность всех перечисленных теорем легко доказать перебором всех возможностей, т. е. методом совершенной индукции. Поскольку переменные в булевой алгебре принимают лишь два значения, то число всех возможных комбинаций значений переменных невелико и проверка выполнения теорем для каждой комбинации не является сложной.

12 3