 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Составление логических схем 12
Удобным способом представления логических выражений являются схемы: переключательные, логические и др.
Задача 2. Составить по данной схеме логическое выражение и упростить его.
Задача 3. Составить логическое выражение F по данной схеме.
В данной логической схеме логические операции И, ИЛИ, НЕ представлены соответствующими обозначениями. Логическое выражение будет следующим:
Задача 4. Вычислить значение F, если А=истина, В=ложь.
Подставим на схеме значения логических переменных А и В, обозначив 1 – истина, 0 – ложь, и вычислим значение F.
Задача 6. По данной комбинационной схеме устройства составить логическое выражение F.
Логические задачи При решении логических задач вначале обозначают простые высказывания как логические переменные латинскими буквами, затем составляют логические выражения и упрощают их с помощью формул преобразования логических выражений (см. выше).
Задача 1. Кто из учеников А, В, С и D играет, а кто не играет в шахматы, если известно следующее: а) если А или В играет, то С не играет; б) если В не играет, то играют С и D; в) С играет.
Решение. Определим следующие простые высказывания: А – «Ученик А играет в шахматы»; В – «Ученик В играет в шахматы»; С – «Ученик С играет в шахматы»; D – «Ученик D играет в шахматы». Запишем сложные высказывания, выражающие известные факты: а) б) с) С. Запишем произведение указанных сложных высказываний:
Упростим эту формулу:
Ответ. В шахматы играют ученики C и D, а ученики A и B – не играют.
Задача 2. Один из трех братьев поставил на скатерть кляксу. На вопрос “Кто это сделал?” получены такие ответы: 1. Алеша: “Витя не ставил кляксу. Это сделал Боря.” 2. Боря: “Это Витя поставил кляксу. Алеша не пачкал скатерть.” 3. Витя: “Боря не мог этого сделать. Я сегодня не готовил уроки.” Оказалось, что двое мальчиков в каждом из двух своих заявлений сказали правду, а один оба раза сказал неправду. Кто поставил кляксу?
Введем обозначения: А – «Алеша поставил кляксу»; В – «Боря поставил кляксу»; V – «Витя поставил кляксу». Запишем теперь суждения мальчиков формулами:
По словам Вити, он не делал сегодня уроки, но это не означает, что он не мог поставить кляксу. Поэтому
По условию задачи, две формулы истинны, а одна ложна. Следовательно, получим
Преобразуем данное логическое выражение:
Таким образом, кляксу поставил Витя.
Лабораторная работа № 3
1. Определить количество строк в таблице истинности для логической функции 2. Определить количество нулей в столбце F таблицы истинности для логической функции 3. Определить количество нулей в столбце истинности для логической функции 4. Определить истинность формулы 5. Определить истинность формулы 6. Определить истинность формулы 7. Упростить логическую формулу и определить её истинность 8. Определить значение формулы 9. Определить значение формулы 10. Упростить логическое выражение (В º С) ® (В ® А). 11. Составить по данной схеме логическое выражение и упростить его.
12. Составить по данной схеме логическое выражение и вычислить его значение при А=истина, В=истина, С=ложь.
13. Построить логическую схему по логическому выражению.
14. По данной комбинационной схеме устройства составить логическое выражение F и упростить его.
12 |
Задача 1. Составить переключательную схему, соответствующую логическому выражению А×В + С×В.
Переключательная схема включает в себя элементы параллельного и последовательного соединений. Параллельное соединение соответствует операции ИЛИ, а последовательное – операции И.
Составим логическое выражение: (А + В)×(В + С×А).
Упростим его: (А + В)×(В + С×А) º А×В + А×С×А + В×В + В×С×А º А×В + 0 + + 0 + В×С×А º А×В + В×С×А.
F = А×В × (В + С).
Задача 5. Составить логическую схему по данному логическому выражению: F = А + В×(С + А).
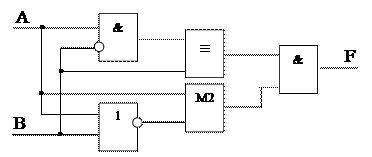
В данной схеме использованы следующие обозначения: & – конъюнкция, 1 – дизъюнкция, º – эквивалентность, М2 – сложение по модулю 2, – отрицание.
;
;
.
2. V × A.
F=(V×B)×(V×A)×B+(V×B)×(V×A)×B+(V×B)×(V×A)×B.
, в которых значение функции F совпадает со значением переменной А.
.
.
.
.
.
.
.
.
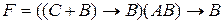