 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Вопрос 2. Ряд геометрической прогрессии
ТЕМА 8. РЯДЫ
ЧИСЛОВЫЕ РЯДЫ 1.Основные понятия числового ряда. 2.Ряд геометрической прогрессии. 3.Основные свойства сходящихся рядов. Остаток ряда. 4.Необходимый признак сходимости числового ряда. 5.Гармонический ряд.
Ряды являются одним из важнейших инструментом математического анализа. С помощью рядов находят приближенные значения функций, интегралов и решений дифференциальных уравнений. Все таблицы, которые вы встречаете в приложениях, составлены с помощью рядов.
Историческая справка Теория числовых и функциональных рядов получила своё развитие в 17-18 столетиях. В те времена еще отсутствовали точные определения основных понятий математического анализа. С рядом, независимо от его сходимости и расходимости, считали возможным обращаться, как с простой суммой. Хотя эта сумма считалась «состоящей из бесконечного числа членов», с ней оперировали как с суммой, состоящей из некоторого (конечного) числа слагаемых. Это приводило подчас к ошибкам в вычислениях, необъяснимым при тогдашнем состоянии математической науки. Суммирование бесконечных геометрических прогрессий со знаменателем меньшим единицы производилось уже в древности (Архимед). Расходимость гармонического ряда была установлена итальянским ученым Менгом в 1650 году, а затем более строго братьями Яковом и Николаем Бернулли. Степенные ряды появились у Ньютона (1665 г.), который показал, что с их помощью можно представить любую функцию. Дальнейшей разработке теории рядов много сил отдавали Лейбниц, Эйлер, Лагранж, Гаусс, Больцано, Коши, Вейерштрасс, Риман и многие другие выдающиеся математики. К числу этих ученых, без сомнения, должен быть отнесен и ученик Ньютона - Тейлор, который опубликовал в 1715 году свой основной труд «Метода приращений, прямая и обратная». В этой книге Тейлор впервые дает вывод разложения в ряд произвольной аналитической функции. Благодаря этому степенной ряд стал тем «мостом», который позволил из области рациональных функций перейти к изучению функций трансцендентных. Однако фундаментальное значение этого вклада в математику было осознано не сразу. В 1742 году вышел знаменитый «Трактат о флюксиях» Колина Маклорена, в котором Маклорен получил новым способом ряд, носящий его имя, и указал, что этот ряд имеется в «Методе приращений». Поскольку Маклорен показал на большом числе функций, что применение этого ряда неизмеримо упрощает задачу разложения функций, то этот ряд, а значит и ряд Тейлора, стали пользоваться большой известностью. Еще больше выросло значение ряда Тейлора, когда в 1772 году Лагранж положил его в основу всего дифференциального исчисления. Он считал, что теория разложения функций в ряды содержит истинные принципы дифференциального исчисления, освобожденные от бесконечно малых и пределов.
Вопрос 1. Основные понятия числового ряда
Само понятие бесконечного ряда по существу не является принципиально новым. Бесконечный ряд представляет собой лишь своеобразную форму числовой последовательности. Однако эта новая форма имеет некоторые особенности, благодаря которым применение рядов более удобно.
Пусть дана бесконечная последовательность чисел a1, a2, …, an,…
О.1.1. Выражение вида
называется числовым рядом или просто рядом. Числа a1, a2, …, an,… называются членами ряда, а число an с произвольным номером n называется общим членом ряда (1).
Ряд (1) считается заданным, если известен общий член ряда an, выраженный как функция его номера n: an = f(n), n=1,2,… Пример 1. Ряд с общим членом
О.1.2. Сумма первых n членов ряда (1) называется n-й частичной суммой ряда и обозначается через Sn, т.е. Sn = a1 + a2 + …+ an.
Рассмотрим последовательность частичных сумм ряда (1): S1 = a1, S2 = a1 + a2, ……., Sn = a1 + a2 + …+ an, …… (2)
О.1.3. Ряд (1) называется сходящимся, если существует конечный предел S последовательности его частичных сумм (2), т.е. Записывается:
Из определения О.1.3 следует, что сумма ряда не обязательно существует. В этом состоит основное отличие бесконечных рядов от конечных сумм: у любой конечной совокупности чисел обязательно существует сумма, «сложить же бесконечное множество чисел оказывается далеко не всегда возможным».
Если Пример 2. 1. Ряд 2. Ряд Вопрос 2. Ряд геометрической прогрессии
О.2.1. Ряд, составленный из членов геометрической прогрессии, т.е. ряд вида
называется рядом геометрической прогрессии или геометрическим рядом. Для краткости ряд (3) называют геометрической прогрессией.
Исследуем сходимость ряда (3). Частичная сумма ряда (3) при q ¹ 1 имеет вид Тогда
В зависимости от величины q возможны следующие случаи:
Случай 1. |q| < 1. Тогда qn ® 0 при n ® ¥ Þ
Случай 2. |q| >1. Тогда qn ® ¥ при n ® ¥ Þ Случай 3. q = 1. Ряд (3) принимает вид a + a + a +…Þ Sn = na и Случай 4. q = ‒1. Ряд (3) принимает вид a – a + a – a +… Þ Вывод.Ряд геометрической прогрессии |



 (1)
(1) имеет вид
имеет вид 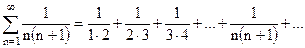
 . В этом случае число S называется суммой ряда (1).
. В этом случае число S называется суммой ряда (1).
 не существует или
не существует или 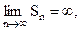 то ряд (1) называется расходящимся. Такой ряд суммы не имеет.
то ряд (1) называется расходящимся. Такой ряд суммы не имеет. сходится и его сумма S = 0.
сходится и его сумма S = 0. расходится, так как
расходится, так как 
 , a ¹ 0,(3)
, a ¹ 0,(3)

 Þ ряд (3) сходится и его сумма
Þ ряд (3) сходится и его сумма 
 Þ ряд (3) расходится.
Þ ряд (3) расходится. Þ ряд (3) расходится.
Þ ряд (3) расходится. Þ
Þ  сходится при |q| < 1 и расходится при |q| ≥ 1.
сходится при |q| < 1 и расходится при |q| ≥ 1.