 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Механические колебания и волны
МЕХАНИКА Указания по выполнению контрольных работ Обучающиеся на заочных подготовительных курсах выполняют три контрольные работы. Представление в университет на проверку и рецензирование контрольной работы № 1 – 15 декабря, работы № 2 – 1 февраля, работы № 3 – 15 марта. Указанные сроки являются крайними. Занятия обучающихся на заочных подготовительных курсах должны быть регулярными и составлять не менее 10 в неделю. Подготовку к выполнению каждой контрольной работы следует начинать с повторения учебного материала по теме контрольной работы. Лучше всего использовать для этой цели на первом этапе учебники по физике для общеобразовательной школы и решать задачи, предлагаемые в конце параграфовов. На втором этапе подготовки к выполнению контрольной работы необходимо воспользоваться различными учебными пособиями и справочными материалами по физике для поступающих в высшие учебные заведения. Уверенное умение решать задачи подобного типа должно стать конечным результатом всей подготовки. Третий этап подготовки – написание рефератов (письменных докладов) по тем вопросам физики, которые указаны в учебной программе и входят в билеты вступительных экзаменов по физике. После этого можно приступать к выполнению контрольных работ. Каждую контрольную работу следует оформлять в отдельной тетради. На обложке тетради должно быть указано место жительства (город, поселок), школа, Ф. И. О., номер и название контрольной работы. В тетради должны быть поля для замечаний и оценок при проверке контрольной работы. Задачи должны быть решены в порядке, соответствующем нумерации в контрольной работе. Условие (словесное) задач можно не переписывать, достаточно указать номер. Решение задачи начать с краткой записи условия под заголовком «Дано», указания искомой величины, собственно решения под заголовком «Решение» (рисунок или график обязателен в каждой задаче) и ответа под заголовком «Ответ». Требования к оформлению и решению задачи указаны в разделе «Алгоритм решения задач…». Учебная литература 1. Мощанский В.Н. Физика-9. 1994. 2. Гончаренко С. У., Воловик П.Н. Физика-10. 1994. 3. Парфентьева Н. А., Фомина М. Ф. Физика. Теория, задачи, решения. (Серия «Библиотека школьника и абитуриента».) Т 1. 1995. 4. Касаткина И. Л., Ларцева Н. А., Шкиль Т. В. Репетитор по физике. Т. 1. 1995. 5. Трофимова Т. И. Сборник задач по курсу физики. 1996. 6. Гольдфарб Н. И. Сборник вопросов и задач по физике. 1995. 7. Бендриков Г. А. и др. Задачи по физике для поступающих в ВУЗы. 1995. 8. Кибец И. Н., Кибец В. И. Физика. Справочник. 1991. 9. Кошкин Н. И. Элементарная физика. Справочник. 1991.
Основы кинематики 1. ВЫПИСКА ИЗ ПРОГРАММЫ Механическое движение. Относительность движения. Система отсчета. Материальная точка. Траектория. Путь и перемещение. Мгновенная скорость. Ускорение. Равномерное и равноускоренное прямолинейные движения. Графики зависимости кинематических величин от времени в равномерном и равноускоренном движениях. Ускорение свободного падения. Движение по окружности с постоянной по модулю скоростью. Центростремительное ускорение.
2. ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ Механическим движениемназывается перемещение тел или их частей в пространстве с течением времени. Всякое движениеотносительно, т. е. необходимо указывать относительно каких тел оно рассматривается. Тело, относительно которого рассматривается движение других тел, называется телом отсчета. Система отсчетасостоит из тела отсчета, системы координат и часов (для задания отсчета времени). Часто в качестве системы координат выбирают прямоугольную(или декартовую) систему координат. Под материальной точкой понимают тело, обладающее массой, размерами которой можно пренебречь по сравнению с пройденным расстоянием. Траекториейназывается линия, которую описывает тело при своем движении. По форме траектории движения бывают криволинейнымиипрямолинейными. При прямолинейном движении траекторией является прямая линия, путь и модуль перемещения равны друг другу. При криволинейном движениитраектория - кривая линия, путь всегда больше модуля перемещения. Частным случаем криволинейного движения является движение по окружности. Путь -это длина траектории. Перемещение -это вектор, соединяющий начальное и конечное положение тела. Скорость -это величина, характеризующая движение и измеряемая отношением пути ко времени: По характеру изменения скорости движения бывают равномерным равнопеременным и неравномерным. Движение, при котором за любые равные промежутки времени тело проходит одинаковые отрезки пути, называется равномерным.Формула пути равномерного движения (т.е. закон движения, или кинематическое уравнение движения) имеет вид: Скорость равномерного движения изображается графически прямой, параллельной оси абсцисс (рис. 1), а путь - прямой, выходящей начала координат и наклонной к оси абсцисс под углом f (рис. 2).
Рис.1 Рис.2
Равнопеременнымназывается такое движение, при котором за единицу времени скорость изменяется на одно и то же постоянное значение. Величина, характеризующая изменение скорости за единицу времени, называетсяускорением. Ускорение выражается формулой: Ускорение и скорость характеризуются не только численным значением, но и направлением, т. е. являются векторами. Если V >V0, то a > 0, и движение называется равноускоренным. Если V < V0, то a < 0, и движение называется равнозамедленным. Графики зависимости скорости от времени при равноускоренном движении (с начальной скоростью V0 и без нее) и при равнозамедленном движении соответственно изображены на рис. 3 и рис. 4.
Рис. 3 Рис. 4
Мгновенная скоростьюнеравномерного движения называется скорость в данный момент времени или в данной точке траектории. Мгновенная скорость для равномерного движения выражается формулой: Средней скоростью неравномерного движения называется скорость такого равномерного движения, при котором тело проходит такой же путь и за такое же время, как и при данном неравномерном движении: Для равнопеременного движения средняя скорость определяется как среднее арифметическое начальной и конечной скоростей: Путь для равнопеременного движения выражается формулой (законом движения): Свободным падением называется падение тела в безвоздушном пространстве под действием силы тяжести. Свободное падение является равноускоренным движением. Высота падения и скорость выражаются формулами: Графически путь равноускоренного движения без начальной скорости численно равен площади треугольника АВС (рис.5), а с начальной скоростью - трапеции АВСD (рис.6).
Рис. 5 Рис.6
При равномерном движении тела по окружности следует различать линейную и угловуюскорости: При равномерном движении тела по окружности угловая скорость постоянна, а линейная постоянна по величине, но переменна по направлению. Следовательно, при равномерном движении по окружности существует ускорение, которое называется центростремительным. Центростремительное ускорение
3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО КИНЕМАТИКЕ 1) Изучив условие задачи, записать его в сокращенном виде. При этом численные значения записать в стандартной форме, единицы измерения физических величин - в СИ. 2) Выбрать систему отсчета (тело отсчета, систему координат с указанием положительного направления осей и момент времени, принимаемый в качестве начального). 3) Сделать рисунок (схематически). Изобразить векторы, соответствующие заданным и искомым физическим величинам. 4) Определить вид движения вдоль каждой координатной оси. Записать кинематические уравнения движения: законы движения (для координат) и законы изменения проекций скорости на каждую из осей. Если движутся несколько тел, то записать уравнения для каждого тела. 5) Определить начальные условия (координаты и проекции скорости в начальный момент времени), а также проекции ускорения на оси и подставить эти величины в кинематические уравнения движения. 6) Определить дополнительные условия (координаты или проекции скорости для какого-то момента времени) и подставить эти величины в кинематические уравнения движения. 7) Полученную систему уравнений решить относительно искомой величины (или величин). 8) Убедиться в справедливости расчетной формулы методом проверки наименований (размерностей) физических величин. 9) Подставить в расчетную формулу численные значения и получить численный результат.
4. ЗАДАЧИ 1. Атомобиль проехал первую половину пути со скоростью V1 = 36 км/ч, а вторую половину - со скоростью V2 = 51 км/ч. Найти среднюю скорость на всем пройденном пути. 2. В тот момент, когда мимо станции проходил товарный состав со скоростью 5 м/с,от платформы в том же направлении отошел пассажирский поезд. Через сколько времени и при какой скорости пассажирский поезд догонит товарный, если он двигался с ускорением 0,5 м/с2, а товарный равномерно? Решить графически и аналитически. 3. С отвесной скалы падает камень. Стук о землю прозвучал через 6 с. Определить высоту скалы. Скорость звука считать равной 330 м/с, а g = 10 м/c2 . 4. Снаряд вылетает из орудия с начальной скоростью 1000 м/с под углом 300 к горизонту. Определить дальность полета и время движения снаряда. Орудие и точка падения снаряда находятся на одном уровне. 5. Стрелок производит выстрел в вертикально стоящую мишень на расстоянии 200 м. На сколько снизится пуля за время полета, если ее начальная скорость 500 м/с ? Основы динамики 1. ВЫПИСКА ИЗ ПРОГРАММЫ Первый закон Ньютона. Инерциальная система отсчета. Масса. Сила. Второй закон Ньютона. Сложение сил. Момент силы. Условия равновесия тел. Третий закон Ньютона. Силы упругости. Закон Гука. Гравитационные силы. Закон Всемирного тяготения. Сила тяжести. Центр тяжести. Движение под действием силы тяжести. Вес тела, движущегося с ускорением по вертикали. Невесомость. Движение искусственных спутников. Расчет первой космической скорости. Силы трения. Коэффициент трения. Принцип относительности Галилея.
2. ОСНОВНЫЕ ПОНЯТИЯ И ФОРМУЛЫ Динамика рассматривает движение тел в пространстве с изменением причин данного движения. Причиной изменения состояния движения (скорости) тел являетсясила. Силой называется величина взаимодействия между телами и полями (гравитационным, электрическим, магнитным), в результате которого происходит изменение состояния движения или деформация. Сила является векторной величиной и характеризуется числовым значением (модулем), направлением и точкой приложения. Силы имеют различную природу. Силы складываются геометрически по правилам сложения векторов. Первый закон Ньютона. Всякое тело сохраняет состояние покоя или прямолинейного равномерного движения, пока действие других тел не выведет его из этого состояния. Свойство тела сохранять состояние покоя или равномерного прямолинейного движения называется инерцией,поэтому первый закон Ньютона называется законом инерции. В природе тело не может быть изолировано от действия других тел и полей. Поэтому относительный покой, прямолинейное и равномерное движение наблюдаются только в том случае, когда результирующая действия всех сил на другое тело равны нулю Закон инерции выполняется в системах отсчета, находящихся в покое или прямолинейном и равномерном движении. Такие системы отсчета получили название инерциальных. Масса - это количество вещества в теле. Масса тела является мерой инертности тела (инертная масса) и физической величиной, описывающей интенсивность взаимодействий в законе всемирного тяготения (гравитационная масса). Второй и третий законы Ньютона справедливы также только в инерциальных системах. Второй закон Ньютонадля движения тела с постоянной массой.Ускорение, сообщаемое телу данной силой, прямо пропорционально величине этой силы и обратно пропорционально массе тела: Поскольку ускорение Произведение силы F на время ее действия t называется импульсом силы, произведение массы движущегося тела на скорость - количеством движения(K = m.V). Следовательно, второй закон Ньютона можно сформулировать следующим образом: изменение количества движения равно импульсу силы. Момент силы относительно оси вращения называется скалярная физическая величина, равная произведению силы на плечо Плечом силы l называется кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Тело, имеющее ось вращения, находится в равновесии, если алгебраическая сумма моментов всех сил равна нулю Третий закон Ньютона. Все тела взаимодействуют друг с другом с силами, равными по величине, но противоположными по направлению, или говорят, что сила действия равна силе противодействия Сила, которая возникает в упруго деформированном теле, называется силой упругости. Упругая деформация - это изменение формы или размеров тела под действием внешней силы, если тело после снятия нагрузки восстанавливает свою форму или размеры. Сила упругости пружины направлена в сторону, противоположную внешней силе, и определяется по закону Гука: Гравитационными силами называют силы притяжения небесных тел, заставляющие их двигаться по определенным траекториям. Закон всемирного тяготения. Два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояний между ними: Коэффициент пропорциональности G называется гравитационной постоянной (численно равна силе притяжения двух материальных точек массой 1 кг каждая, находящихся на расстоянии 1 м; Все тела притягиваются Землей. Под действием гравитационной силы Сила, с которой тела притягиваются к Земле, называется силой тяжести.Под действием силы тяжести все тела падают на Землю и давят на ее поверхность. Сила тяжести равна разности между силой тяготения (гравитации) и центростремительной силой: Центром тяжести тела называется точка, относительно которой моменты сил действующих на тело равны нулю. Весом тела называется сила, с которой тела вследствие притяжения к Земле действуют на горизонтальную опору или вертикальный подвес. Эта сила приложена к опоре или подвесу. Если тело движется вертикально вверх с ускорением, то вес тела Силы, препятствующие движению одного тела по поверхности другого, называются силами трения.Различают трения: покоя, скольжения и качения. Независимо от типа трения сила трения находится по формуле:
3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ 1) Изучив условие задачи, записать его в сокращенном виде. При этом численные значения записать в стандартной форме, единицы измерения физических величин - в СИ 2) Выбрать инерциальную систему отсчета. 3) Сделать рисунок (схематически). Найти все силы, действующие на тело, и изобразить их. Изобразить также ускорение. 4) Определить вид движения тела. Записать второй закон Ньютона (уравнение движения) в векторной форме, в котором под силой понимают результирующую силу всех сил. Если движутся несколько тел, то записать уравнения для каждого тела. 5) Перейти к скалярной форме записи, заменив все векторы их проекциями на координатные оси. 6) Выразить силы через физические величины, от которых они зависят, воспользовавшись соответствующими законами (законы Гука, Всемирного тяготения и т.д.) и подставить выражения в уравнение движения. 7) Если в задаче требуется определить (или, наоборот, даны) координаты или скорость тела, записать и кинематические уравнения движения. 8) Полученную систему уравнений решить относительно искомой величины. 9) Убедиться в справедливости расчетной формулы методом проверки наименований (размерностей) физических величин. 10) Подставить в расчетную формулу численные значения и получить численный результат. 4. ЗАДАЧИ 1. Рассчитать первую космическую скорость. 2. Человек массой 70 кг поднимается в лифте, движущимся равнозамедленно вертикально вверх с ускорением 1 м/c2. Определить силу давления человека на пол кабины лифта. 3. Груз массой 45 кг перемещается в горизонтальной плоскости под действием силы в 294 Н, направленной под углом 30о к горизонту. Коэффициент трения о плоскость 0,1. Определить ускорение. 4. Груз массой 50 кг равноускоренно поднимается с помощью каната вертикально вверх в течение 2 с на высоту 10 м. Определить силу натяжения каната. 5. Автомобиль массой 1000 кг поднимается по шоссе с уклоном 30о, под действием силы тяги 7 кН. Коэффициент трения между шинами и поверхностью шоссе 0,1. Найти ускорение автомобиля.
Законы сохранения 1. ВЫПИСКА ИЗ ПРОГРАММЫ Импульс тела. Закон сохранения импульса. Реактивное движение. Устройство ракеты. Значение работ К. Э. Циолковского для космонавтики. Достижения страны в освоении космического пространства. Механическая работа. Потенциальная и кинетическая энергии. Закон сохранения механической энергии. 2. ОСНОВНЫЕ ФОРМУЛЫ · Импульс (количество движения) тела (или материальной точки) ® ® p = m × v .
· Закон сохранения импульса для замкнутой системы тел ® n ® p = å mi × vi = const , i=1 ® ® ® ® ® pI= pII, или D p = pII- pI= 0 ,
где n - число тел, образующих систему, p - суммарный импульс системы, pIи pII - суммарные импульсы системы тел до и после взаимодействия. · Скорости двух тел массами m1и m2 после абсолютно упругого центрального удара ® ® ® (m1- m2) × v1 + 2 × m2 × v2 u1 = ¾¾¾¾¾¾¾¾¾¾¾ , m1 + m2
® ® ® (m2- m1) × v2 + 2 × m1× v1 u2 = ¾¾¾¾¾¾¾¾¾¾¾ , m1 + m2
где v1 и v2 - скорости тел до удара. · Скорость движения тел после центрального абсолютно неупругого удара ® ® ® m1× v1 + m2× v2 u =¾¾¾¾¾¾¾¾ . m1 + m2
· Уравнение движения тела переменной массы (уравнение Мещерского) ® ® ® m × a = F + Fр.
· Реактивная сила ® ® Fр=- u ×(dm / d t), ® где u - скорость истечения газов из ракеты. · Формула Циолковского для определения скорости ракеты ® ® v = u × ln (M/m), где M - начальная масса ракеты. · Работа, совершаемая постоянной силой, ® ® A =(F × s) = Fs × s =F × s × cos a , ® где Fs - проекция силы на направление перемещения s, a - угол между направлениями силы и перемещения. · Элементарная работа ® ® dA = (F × ds) = Fs ×ds = F × cos a × ds ,
где ds - вектор элементарного (физически бесконечно малого) перемещения. · Работа, совершаемая переменной силой, на пути s ® ® A = ò(F × ds) = ò Fs ×ds = ò F × cos a × ds . s s s · Средняя мощность за интервал времени Dt
<N> = A / Dt .
· Мгновенная мощность ® ® N = dA / dt , или N = (F × v) = Fs × v = F × v× cos a .
· Кинетическая энергия тела массой m
T = m × v2 / 2.
· Потенциальная энергия тела, поднятого над поверхностью Земли на высоту h П = m × g × h .
· Потенциальная энергия упруго деформированного тела (сжатой пружины жесткостью k)
П = k × x2 / 2 .
· Закон сохранения механической энергии (для замкнутой системы, внутри которой действуют только консервативные силы)
Т + П = Е = const , или ЕI = ЕII =const, или D Е = ЕII- ЕI =0 ,
где ЕI и ЕII- механические энергии двух состояний системы тел. · Закон сохранения и изменения механической энергии (для замкнутой системы, внутри которой действуют и неконсервативные силы)
DЕ = ЕII- ЕI= A ,
где A - работа неконсервативных сил (например, силы трения).
3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА 1) Изучив условие задачи, записать его в сокращенном виде. При этом численные значения записать в стандартной форме, единицы измерения физических величин - в СИ. 2) Выбрать систему отсчета. 3) Сделать 2 рисунка (схематически) непосредственно до и после взаимодействия тел. Изобразить импульсы (или скорости) тел. 4) Выяснить систему взаимодействующих тел и то, какие силы для нее являются внешними, а какие - внутренними. 5) Если в целом система не замкнута (есть результирующая внешняя сила), но проекция результирующей силы на какую-либо ось равна нулю, то приме нить закон сохранения импульса в проекциях на эту ось. 6) Если взаимодействие тел имеет характер удара (является кратковременным), то сначала можно использовать закон сохранения импульса в векторной форме, а затем перейти к скалярной форме. 7) Если в задаче требуется найти не импульс (или скорость) тела после взаимодействия, а другие физические величины (например, перемещение), то надо записать и другие соответствующие физические законы. 8) Систему уравнений решить относительно искомой величины. 9) Убедиться в справедливости расчетной формулы методом проверки наименований (размерностей) физических величин. 10) Подставить в расчетную формулу численные значения и получить численный результат.
4. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙ ЭНЕРГИИ 1) Изучив условие задачи, записать его в сокращенном виде. При этом численные значения записать в стандартной форме, единицы измерения физических величин - в СИ. 2) Выбрать систему отсчета. Изобразить нулевой уровень отсчета потенциальной энергии. 3) Выбрать 2 состояния тела (или системы тел) так, чтобы состояния характеризовались как известными, так и искомыми величинами. Сделать соответственно 2 рисунка. 4) Выяснить, какие силы действуют на систему тел: потенциальные или непотенциальные. 5) Если действуют только потенциальные силы, то применить закон сохранения механической энергии. Если действуют и непотенциальные силы (например, сила трения), то применить закон сохранения и изменения механической энергии. 6) Выразить механическую энергию в каждом состоянии как сумму кинетической и потенциальной энергий. Подставить соответственно выражения для кинетических и потенциальных энергий этих состояний и решить уравнение относительно искомой величины. 7) Убедиться в справедливости расчетной формулы методом проверки наименований (размерностей) физических величин. 8) Подставить в расчетную формулу численные значения и получить численный результат. 5. ЗАДАЧИ 1. С самоходной артиллерийской установки, движущейся со скоростью v = = 54 км/ч, произведен выстрел под углом a = 60° к горизонту в направлении, противоположном движению установки. Снаряд вылетел со скоростью u = 1 км/с. На сколько изменилась скорость установки (Dv - ?), если масса установки m = 200 т, а масса снаряда m = 50 кг? 2. На нити длиной l = 2 м висит небольшой ящик с песком массой M = 2 кг. Пуля, летящая горизонтально, попадает в ящик и застревает в нем, при этом максимальное отклонение нити составляет 30° . Определить начальную скорость пули, если масса пули m = 10 г. Это устройство называется баллистическим маятником. (Раньше оно использовалось для определения скорости пуль). Размеры ящика существенно меньше длины нити. 3. Два шара массами m1 = 200 г и m2 = 400 г подвешены на нитях длиной l = = 67,5 см. Первоначально шары соприкасаются между собой, затем первый шар отклонили от положения равновесия на угол 60° и отпустили. Определить, на какую высоту поднимется второй шар после удара, если: а) удар абсолютно упругий; б) удар абсолютно неупругий. 4. Автоматический пистолет имеет подвижный кожух. Кожух и корпус соединяются пружиной. Коэффициент жесткости равен 32 Н/м, масса кожуха - 500 г, масса пули - 10 г. При выстреле кожух сжимает пружину и отходит назад на 1 см. Найти скорость пули при вылете из ствола. 5. Бронетранспортер массой 3 т, начиная движение, проходит первые 75 м за 20 с. Коэффициент сопротивления движению равен 0,05. Найти работу двигателя. 6. Тело массой 200 г брошено горизонтально со скоростью 10 м/с. Найти кинетическую энергию тела через 2 с после бросания. Сопротивлением воздуха пренебречь. 7. Тело, падая с некоторой высоты, в момент соприкосновения с землей имеет импульс p = 100 кг м/с и кинетическую энергию Т = 500 Дж. Определить: а) высоту падения тела; б) массу тела. 8. Пуля массой 10 г, летящая со скоростью 500 м/c, пробивает доску толщиной 50 см и вылетает со скоростью 200 м/c. Определить среднюю силу сопротивления, которая действовала на пулю. 9. Двухступенчатая ракета массой 940 кг движется со скоростью 6,2 км/с относительно земли. Затем происходит запланированный взрыв, в результате которого ракета разделяется на две части одинаковой массы. Относительная скорость движения частей вдоль линии первоначального движения равна 2,4 км/c. Определить: а) значения и направления скоростей каждой части сразу после взрыва; б) количество энергии, выделившееся при взрыве. 10. В реактивный двигатель самолета поступает 100 кг воздуха, которые сгорают ежесекундно вместе с 4,2 кг топлива. Продукты сгорания в виде газов выбрасываются из сопла со скоростью 550 м/c (относительно самолета). Самолет движется со скоростью 270 м/с. Определить: а) результирующую силу тяги двигателя; б) развиваемую двигателем мощность (в лошадиных силах).
Жидкости и газы 1. ВЫПИСКА ИЗ ПРОГРАММЫ Давление. Закон Паскаля для жидкостей и газов. Сообщающиеся сосуды и их применение. Гидравлический пресс. Атмосферное давление. Опыт Торричелли. Барометр-анероид. Изменение атмосферного давления с высотой. Манометры. Насосы. Архимедова сила. Условия плавания тел. Водный транспорт. Воздухоплавание. Зависимость давления жидкости от скорости ее течения. Подъемная сила крыла самолета.
2. ОСНОВНЫЕ ФОРМУЛЫ · Гидростатическое давление столба жидкости на глубине h
p = r × g × h ,
где r - плотность жидкости. · Закон Архимеда FA = r × g × V ,
где V - объем вытесненной жидкости. · Подъемная сила Fпод = FA - m × g ,
где m - масса поднимающегося тела. · Условие плавания тела
Fпод = 0 , или FA = m g = P1 - P2,
где P1 - вес тела в воздухе, P2 - вес тела в жидкости (P1 > P2). · Уравнение Бернулли для стационарного течения идеальной несжимаемой жидкости r × v2 / 2 + r × g × h + p = const , или r × v12 / 2 + r × g × h1 + p1 = r × v22 / 2 + r × g × h2 + p2,
где p - статическое давление жидкости для определенного сечения трубки тока, v - скорость жидкости для этого же сечения, r × v2 / 2 -
динамическое давление (динамический напор) жидкости этого же сечения, h - высота, на которой расположено сечение, индексы "1" и "2" относятся к двум разным сечениям трубки тока. · Уравнение Бернулли для горизонтальной трубки тока
r × v2 / 2 + p = const .
· Формула Торричелли для определения скорости истечения жидкости из малого отверстия в открытом широком сосуде
v = Ö 2 × g × h ,
где h - глубина отверстие относительно уровня жидкости в сосуде. · Подъемная сила крыла самолета
R = C × (r × v2 / 2) × S ,
где C - безразмерный коэффициент подъемной силы, r - плотность среды, v - скорость движения тела, S - площадь наибольшего поперечного сечения тела.
3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ ПО МЕХАНИКЕ ЖИДКОСТЕЙ И ГАЗОВ 1) Изучив условие задачи, записать его в сокращенном виде. При этом численные значения записать в стандартной форме, единицы измерения физических величин - в СИ. 2) Необходимо помнить, что законы и формулы этой темы являются следствиями основных законов механики (законов Ньютона, закона сохранения энергии, закона сохранения массы). Выяснить природу сил давления жидкости (или газа) на стенки сосуда, в котором находится жидкость, или на поверхность твердого тела, находящегося в жидкости. Сделать рисунок, изобразив эти силы. 3) Если на рассматриваемую поверхность действуют как внутренние силы (например, сила тяжести столба жидкости), так и внешние, то общее давление равно сумме внутреннего и внешнего давлений. 4) Последующий алгоритм решения задач аналогичен рассмотренным выше алгоритмам. 4. ЗАДАЧИ 1. К малому поршню гидравлического пресса приложена сила 200 Н. Малый поршень опускается на 25 см за один ход, а большой поршень поднимается на 5 мм. Найти: а) силу давления на большой поршень; б) работу, совершаемую за один ход поршней. 2. Со дна озера глубиной 5 м поднимают мину на поверхность воды. Плотность воды 1000 кг/м3, средняя плотность мины 2500 кг/м3 , объем мины 0,6 м3 . Найти работу по подъему мины. 3. Тело массой m и объемом V брошено вертикально вниз с высоты H с начальной скоростью v0 . На какую глубину h погрузится тело? Сопротивлением воздуха и воды пренебречь. 4. Прямоугольный понтон массой 800 кг имеет длину 4 м, ширину 2 м и высоту 70 см. Найти: а) осадку (глубину погружения) h понтона без нагрузки; б) высоту бортов над уровнем воды Dh после принятия груза массой 3,2 т. 5. Аэростат массой 500 кг и объемом 600 м3 начинает подниматься вертикально вверх. Считая плотность воздуха постоянной и равной 1,3 кг/м3, определить, на какой высоте окажется аэростат через 1 с. 6. В бак равномерной струей за 1 с поступает 2 дм3 воды. В дне бака имеется отверстие площадью 2 см2. На какой высоте будет свободная поверхность воды?
Механические колебания и волны 1. ВЫПИСКА ИЗ ПРОГРАММЫ Колебательное движение. Свободные колебания. Амплитуда, период, частота и фаза колебаний. Математический маятник. Формула периода колебаний математического маятника. Колебания груза на пружине. Превращение энергии при колебательном движении. Вынужденные колебания. Резонанс. Распространения колебаний в упругих средах. Поперечные и продольные волны. Связь длины волны со скоростью ее распространения, периодом (частотой). Звуковые волны. Скорость звука. Громкость звука, высота тона. 2. ОСНОВНЫЕ ФОРМУЛЫ · Закон свободных гармонических колебаний груза, выведенного из положения равновесия, x (t) = A × cos (w × t + j 0) ,
где x (t) - смещение тела в данный момент времени от положения равновесия, A - амплитуда колебаний, w - собственная циклическая частота колебаний маятника, j 0 - начальная фаза колебаний. · Уравнение свободных гармонических колебаний груза ×× m × a = - k × x , или x + w2 × x = 0,
где w = k/m , k - коэффициент возвращающей силы (равен жесткости пружины для пружинного маятника, а для математического маятника - g/l, l - длина нити). · Циклическая частота w = 2 × p / T .
· Период колебаний T = N / t ,
где N - число колебаний за время t . Период колебаний соответственно математического и пружинного маятников: ¾Ø ¾Ø T = 2 × p Ö l / g и T = 2 × p Ö m / k .
· Частота колебаний n = 1/ T .
· Скорость груза, совершающего гармонические колебания, . v (t) = x = - A × w × sin (w × t + j 0 ) , или . v (t) = x = A × w × cos (w × t + j 0 + p/2) .
· Ускорение груза, совершающего гармонические колебания, ×× a (t) = x = - A × w 2 × cos (w × t + j 0) , или ×× a (t) = x = - A × w2 × x (t) .
· Кинетическая энергия груза массой m, колеблющегося гармонически,
T (x) = (1/2) × m × A2 × w2 × sin (w × t + j 0) .
· Потенциальная энергия гармонических колебаний груза
П (x) = (1/2) × m × A2 × w2 × cos (w × t + j 0) .
· Полная энергия механических гармонических колебаний
Е = (1/2) × m × A2 × w2 = const.
· Вынуждающая сила F (t) = Fmax × cos (W × t) ,
где Fmax и W - амплитуда и частота вынуждающей силы. · Закон вынужденных установившихся колебаний
x (t) = A × cos (W × t + j 0) ,
· Уравнение вынужденных механических колебаний
m × a = - k × x - r × v + Fmax × cos (W × t), .. . или x + 2 × d × x + w2 × x = F max × cos (W × t) ,
где d = r/(2×m) - коэффициент затухания колебаний, r - коэффициент сопротивления. · Амплитуда вынужденных колебаний Fmax A = ¾¾¾¾¾¾¾¾¾¾¾¾ . m × Ö (w2 - W2 )2 + 4 × d2 × w2
· Резонансная амплитуда Fmax Aрез = ¾¾¾¾¾¾¾¾ . 2 × m×d× Ö w2 - d2
· Резонансная частота wрез = Ö w2 - 2 × d2 .
· Связь длины волны и периода (частоты) колебаний частиц в упругой волне l = v × T = v / n ,
где v - фазовая скорость распространения колебаний в среде. · Уравнение плоской волны, распространяющейся вдоль положительного направления оси x
x (x , t) = A × cos (w × t - k × x + j 0) ,
где x (x , t) - смещение точек с координатой x в момент времени t , A - амплитуда волны, k - волновое число. · Волновое число k = 2 × p / l .
· Связь между разностью фаз колебаний частиц и разностью хода луча волны Dj = 2 × p × (Dx / l) .
3. АЛГОРИТМ РЕШЕНИЯ ЗАДАЧ НА МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ и ВОЛНЫ подобен алгоритму решения задач по кинематике и динамике.
4. ЗАДАЧИ 1. Тело совершает, колебания по закону x (t) = 0,3 × cos (p × t + p/2) м. Найти: амплитуду, период, начальную фазу, полную энергию колебаний, а также ускорение, кинетическую и потенциальную энергии в момент времени 0,5 с после начала колебаний. 2. Математический маятник, состоящий из нити длиной l = 1 м и свинцового шарика радиусом r = 2 см, совершает гармонические колебания с амплитудой 6 см. Плотность свинца r = 11,3 г/см3. Определить: а) скорость шарика при прохождении им положения равновесия; б) максимальное значение возвращающей силы. 3. Пружина имеет жесткость 25 Н/м. Определить, груз какой массы m надо подвесить к пружине, чтобы за 1 мин совершалось 25 колебаний. 4. На идеально гладкой плоскости лежит брусок массой M, прикрепленный к стене посредством горизонтально расположенной пружины. Жесткость пружины равна k, масса пружины пренебрежимо мала. В брусок попадает пуля массой m, летящая горизонтально со скоростью v, и застревает в нем. Найти: а) зависимость координаты от времени (закон колебаний бруска) после попадания пули; б) зависимость скорости колебаний бруска от времени. Считать момент попадания пули в брусок за начало отсчета времени. 5. Груз массой m = 50 г, подвешенный на нити длиной l = 20 см, совершает колебания в вязкой среде (в жидкости). Коэффициент сопротивления r = = 0,02 кг/с. На груз действует вынуждающая сила F = 0,1× cos (W×t) Н. Опре - делить: а) резонансную частоту; б) резонансную амплитуду. 6. Источник возбуждает в упругом шнуре волны длиной 0,35 м. Частота колебаний 1000 Гц , амплитуда колебаний 0,5 мм. Во сколько раз скорость распространения колебаний (фазовая скорость) отличается от максимальной скорости колеблющихся частиц? 7. В упругой среде распространяется волна со скоростью v = 720 м/с. Частота источника равна n = 600 Гц. Найти разность фаз (Dj) колебаний двух точек среды, отстоящих друг от друга на расстоянии Dx = 20 см. 8. Выстрел произведен вертикально вверх. Звук выстрела и пули достигают одновременно высоты h = 850 м. Скорость звука в воздухе равна 340 м/с. Найти начальную скорость пули v0 .
|



 где S - путь, t - время.
где S - путь, t - время. где V - скорость, t - время.
где V - скорость, t - время.
 где V - конечная скорость, V0 - начальная скорость, t - время.
где V - конечная скорость, V0 - начальная скорость, t - время.
 где a - ускорение, V0 - начальная скорость, t - время. Если V0 = 0 , то
где a - ускорение, V0 - начальная скорость, t - время. Если V0 = 0 , то 

 . Если подставить в эту формулу выражение
. Если подставить в эту формулу выражение 
 , или
, или 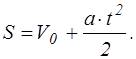 Если V0 = 0 , то
Если V0 = 0 , то 

 где g=9,8 м/c2- ускорение свободного падения. Если V0 = 0 , то
где g=9,8 м/c2- ускорение свободного падения. Если V0 = 0 , то 


 линейная, а
линейная, а  угловая, где a -угол поворота радиус-вектора, проведенного из центра окружности к телу.
угловая, где a -угол поворота радиус-вектора, проведенного из центра окружности к телу. , или
, или 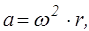 где
где 

 или
или  где a - ускорение; F - действующая сила или равнодействующая нескольких сил; m = const - масса тела. Ускорение является векторной величиной, направление которой совпадает с направлением действующей силы.
где a - ускорение; F - действующая сила или равнодействующая нескольких сил; m = const - масса тела. Ускорение является векторной величиной, направление которой совпадает с направлением действующей силы. то формулу второго закона Ньютона (или уравнение поступательного движения) можно записать в виде:
то формулу второго закона Ньютона (или уравнение поступательного движения) можно записать в виде:  , или
, или 


 .
. где k - коэффициент жесткости, x - удлинение пружины. Коэффициент жесткости численно равен силе, вызывающей единичную деформацию.
где k - коэффициент жесткости, x - удлинение пружины. Коэффициент жесткости численно равен силе, вызывающей единичную деформацию. где r- расстояние между центрами масс тел.
где r- расстояние между центрами масс тел. м3/кг.с2.
м3/кг.с2. тело будет свободно падать.
тело будет свободно падать. Центростремительная сила является силой инерции, обусловленной выбором системы отсчета, которая связана с поверхностью вращающейся Земли. Поскольку эта сила достаточно мала по сравнению с силой тяжести, то для решения задач можно пользоваться упрощенной формулой
Центростремительная сила является силой инерции, обусловленной выбором системы отсчета, которая связана с поверхностью вращающейся Земли. Поскольку эта сила достаточно мала по сравнению с силой тяжести, то для решения задач можно пользоваться упрощенной формулой 
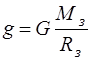 , где m- масса тела, g - ускорение свободного падения. Ускорение свободного падения не зависит от массы тела, но зависит от широты местности. Поэтому оно одинаково для всех тел, расположенных на данной широте.
, где m- масса тела, g - ускорение свободного падения. Ускорение свободного падения не зависит от массы тела, но зависит от широты местности. Поэтому оно одинаково для всех тел, расположенных на данной широте. оказывается больше силы тяжести на величину m.a; если вниз, то
оказывается больше силы тяжести на величину m.a; если вниз, то  , т.е. меньше силы тяжести; если a = g, то тело испытывает невесомость.
, т.е. меньше силы тяжести; если a = g, то тело испытывает невесомость. где k - коэффициент трения, N - сила нормального давления. Коэффициент трения величина безразмерная, определяется опытным путем и зависит от состояния трущихся поверхностей.
где k - коэффициент трения, N - сила нормального давления. Коэффициент трения величина безразмерная, определяется опытным путем и зависит от состояния трущихся поверхностей.