 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Равновесие при абсорбции. Закон Генри. 12
Массообменные Процессы и аппараты Лекция 9
1.7.2 Технологический расчет аппарата со ступенчатым контактом фаз.
Особенность процесса – существенная дискретная неоднородность удельной поверхности контакта фаз по высоте аппарата. Кроме того, в большинстве случаев для них не приемлемо допущение о параллельном движении фаз в режиме идеального вытеснения, которое использовалось при выводе основного уравнения массопередачи. Рассмотрим схему проектного технологического расчёта массообменного аппарата со ступенчатым контактом фаз на примере тарельчатой колонны с противоточным движением газовой и жидкой фаз (рис.1.10). Расход жидкой фазы
Рис. 1.10. Изменение концентраций фаз по высоте тарельчатой колонны (а) и схема тарелки (б)
Высоту колонны можно связать с числом тарелок N и межтарельчатым расстоянием
Величина Основная задача – определение N, обеспечивающих необходимый перенос распределяемого компонента из одной фазы в другую. Для этого вводится понятие эффективности тарелки по Мэрфри (кпд тарелки)
где Если Следует отметить, что при этом составы фаз рассматриваются в различных сечениях аппарата ( Рассмотрим различные способы определения число тарелок N.
Потарелочный расчёт колонны. Это аналитический метод определения N основан на решение уравнений материального баланса, равновесия и использования эффективности по Мэрфи для каждой тарелки. Для нижней тарелки под номером 1составы фаз известны Рассмотрим вторую тарелку. Запишем необходимые уравнения:
уравнение равновесия уравнение Мэрфри уравнение рабочей линии
Итак нашли составы фаз для тарелки 2. Далее, также для 3 тарелки и т.д. Для тарелки
Расчёт заканчивается при значении l, для которого начинает выполняться условие Для ориентировочных расчётов, выполняемых вручную, используют упрощенные графические способы нахождения числа тарелок.
Определение числа тарелок с помощью кинетической кривой.
Эффективность по Мэрфри рассчитывается не для каждой тарелки, а лишь для нескольких сечений колонны, аналитическое решение уравнений (1.64-1.69) заменяется графическим.
Алгоритм действий следующий: — строятся рабочая и равновесная линии; — для нескольких сечений аппарата (нескольких рабочих концентраций —находят величины.
— на диаграмме х – у наносятся точки — из точки Таким образом, аналитическое решение заменяется графическим определением число ступеней лестницы.
Рис.1.11. Определение числа тарелок с помощью кинетической кривой: 1 – рабочая линия, 2 – равновесная линия, 3 – кинетическая кривая. Определение числа тарелок с помощью кпд колонны
Кпд колонны:
где Алгоритм действий следующий: - аналитическим или графическим способом определяется - по известным эмпирическим формулам рассчитывается к.п.д. колонны - по формуле (1.71) находят необходимое
АБСОРБЦИЯ.
Абсорбцией называется процесс избирательного поглощения газов или паров из газовых или парогазовых смесей жидким поглотителем – абсорбентом. Если поглощаемый газ – абсорбтив – химически не взаимодействует с абсорбентом, то такая абсорбция физическая, если же абсорбтив образует с абсорбентом химическое соединение, то такой процесс называется хемосорбцией. Физическая абсорбция обратима, выделение поглощаемого газа из раствора – десорбция. Сочетание абсорбции и десорбции позволяют многократно использовать поглотитель и выделять поглощённый газ в чистом виде. Инертный газ – компонент газовой смеси не переходящий границу раздела фаз. Абсорбция применяется: - для получения готового продукта (абсорбция - для выделения ценных компонентов из газовых смесей (абсорбция бензола из коксового газа, абсорбция ацетилена из газов крекинга или пиролиза природного газа и т.д.), при этом абсорбцию проводят в сочетании с десорбцией; - для очистки газовых выбросов от вредных примесей; - для осушки газов.
Равновесие при абсорбции. Закон Генри. Система состоит из трёх компонентов (распределяемое вещество А и два распределяющих вещества) и двух фаз – жидкой и газовой. Такая система по правилу фаз имеет три степени свободы: Для абсорбции переменными являются Т, Р, концентрация компонента А в газовой и жидкой фазах. Следовательно, в состоянии равновесия при Т=const и постоянном общем давлении Р зависимость между парциальным давлением газа Эта зависимость выражается законом Генри (связана с равновесной линией): парциальное давление
где Растворимость газа в жидкости при данной температуре пропорционально его парциальному давлению над жидкостью:
Здесь
Рис.2.1 Растворимость газа в жидкость от Т.
Для идеальных растворов на диаграмме р–х (рис.2.1) зависимость равновесных концентраций от давления изображается прямой, с наклоном, равным Е. Как видно из рис.2.1,чем больше Т, тем меньше растворимость. Если
Тогда, из уравнений (2.1) и (2.3) получим:
Итак для закона Генри имеем:
Здесь Величина m уменьшается с увеличением Р и снижения Т. См Рис.2.1 12 |



 , его конечная концентрация, диаметр аппарата
, его конечная концентрация, диаметр аппарата  и скорости движения фаз
и скорости движения фаз  и
и  определяется также, как и для аппарата с непрерывным контактом фаз.
определяется также, как и для аппарата с непрерывным контактом фаз.
 :
: (1.62)
(1.62) , являясь одним из параметров оптимизации, в первом приближении может определяться из условия максимально допустимого уноса капель газовым потоком. Для различных типов тарелок имеются соотношения связывающие величину уноса с
, являясь одним из параметров оптимизации, в первом приближении может определяться из условия максимально допустимого уноса капель газовым потоком. Для различных типов тарелок имеются соотношения связывающие величину уноса с  и скоростью газовой фазы
и скоростью газовой фазы  , характеризующее степень достижения равновесия между уходящими с тарелки фазами:
, характеризующее степень достижения равновесия между уходящими с тарелки фазами: (1.63)
(1.63) - концентрация распределяемого компонента в газовой фазе, равновесная с уходящим с l-ой тарелки потоком жидкости. Аналогичным образом можно найти
- концентрация распределяемого компонента в газовой фазе, равновесная с уходящим с l-ой тарелки потоком жидкости. Аналогичным образом можно найти  , используя концентрации жидкой фазы.
, используя концентрации жидкой фазы. , то такую тарелку называют теоретической. Т.е. имеем такой объём аппарата, концентрация распределяемого вещества на выходе из которого
, то такую тарелку называют теоретической. Т.е. имеем такой объём аппарата, концентрация распределяемого вещества на выходе из которого  равна равновесной концентрации на входе в него:
равна равновесной концентрации на входе в него:  . В этом объёме аппарата происходит процесс полного (теоретического) обмена распределяемого вещества между обеими фазами.
. В этом объёме аппарата происходит процесс полного (теоретического) обмена распределяемого вещества между обеими фазами. - над l-ой тарелкой,
- над l-ой тарелкой,  - под ней). Таким образом, в любом поперечном сечении аппарата равновесие не достигается
- под ней). Таким образом, в любом поперечном сечении аппарата равновесие не достигается  , иначе отсутствовала бы движущая сила массопередачи.
, иначе отсутствовала бы движущая сила массопередачи. .
. , (1.64)
, (1.64) , (1.65)
, (1.65) , (1.66)
, (1.66)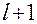 имеем:
имеем: (1.67)
(1.67) (1.68)
(1.68) (1.69)
(1.69) , при этом число тарелок N=l. Поскольку число тарелок в аппарате может достигать сотни и более, данный алгоритм необходимо реализовать на компьютере.
, при этом число тарелок N=l. Поскольку число тарелок в аппарате может достигать сотни и более, данный алгоритм необходимо реализовать на компьютере. ;
;  ;
;  ) рассчитываются эффективности по Мерфри
) рассчитываются эффективности по Мерфри 

 (1.70)
(1.70) и т.д. Соединяя их получим кинетическую кривую.
и т.д. Соединяя их получим кинетическую кривую. спускаемся по лестнице до тех пор, пока для точки
спускаемся по лестнице до тех пор, пока для точки  не выполнится условие
не выполнится условие  . На этом построение заканчивается, необходимое число тарелок в колонне
. На этом построение заканчивается, необходимое число тарелок в колонне  .
.
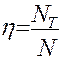 (1.71)
(1.71) - теоретическое число тарелок, N – действительное число тарелок. Величина
- теоретическое число тарелок, N – действительное число тарелок. Величина  находится из опыта. Найти
находится из опыта. Найти  опытным путём достаточно сложно. Необходимы данные по идентичной колонне.
опытным путём достаточно сложно. Необходимы данные по идентичной колонне. .
. .
. .
. в производстве серной кислоты, абсорбция HCl, оксидов азота водой в производстве азотной кислоты);
в производстве серной кислоты, абсорбция HCl, оксидов азота водой в производстве азотной кислоты); .
. или его концентрацией и составом жидкой фазы однозначна.
или его концентрацией и составом жидкой фазы однозначна. в растворе:
в растворе: (2.1)
(2.1) - парциальное давление поглощаемого газа над раствором, находящегося в равновесии, при концентрации раствора
- парциальное давление поглощаемого газа над раствором, находящегося в равновесии, при концентрации раствора  , Е – константа Генри. Е не зависит от общего давления в системе, но зависит от природы абсорбента и поглощаемого газа, а также от Т.
, Е – константа Генри. Е не зависит от общего давления в системе, но зависит от природы абсорбента и поглощаемого газа, а также от Т. (2.2)
(2.2) - концентрация газа в растворе, равновесная с газовой фазой, в которой парциальное давление поглощаемого компонента равна
- концентрация газа в растворе, равновесная с газовой фазой, в которой парциальное давление поглощаемого компонента равна  .
.

 – молярная доля извлекаемого компонента А в газовой смеси и Р – общее давление в системе, то парциальное давление
– молярная доля извлекаемого компонента А в газовой смеси и Р – общее давление в системе, то парциальное давление  , по закону Дальтона, можно записать:
, по закону Дальтона, можно записать: (2.3)
(2.3)
 (2.4)
(2.4) - коэффициент распределения, или константа фазового равновесия.
- коэффициент распределения, или константа фазового равновесия.