 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной
Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Классическое, статистическое и геометрическое определение вероятности события.
Подвероятностью события А понимается математическая (количественная) оценка возможности появления этого события в результате опыта. Определение. (Классическое определение вероятности) Вероятность события Аравна отношению числа исходов опыта, благоприятствующих событию А, к общему числу попарно несовместных исходов опыта, образующих полную группу событий.
Здесь P(A) – вероятность события А m – число исходов опыта, благоприятствующих событию А n – общее число исходов опыта. Очевидно, что для достоверного события m = n, для невозможного события m = 0,для случайного события 0 < m < n. Таки образом, справедливо утверждение: Вероятность достоверного события равна единице, вероятность невозможного – равна нулю, вероятность случайного события выражается числом, расположенным между нулем и единицей. Значение вероятности любого события – есть положительное число, заключенное между нулем и единицей.
Пример. В коробке находится 10 шаров. 3 из них красные, 2 – зеленые, остальные белые. Найти вероятность того, что вынутый наугад шар будет а) красным, б) зеленым, в) белым.
Появление красного, зеленого и белого шаров составляют полную группу событий. Обозначим появление красного шара – событие А, появление зеленого – событие В, появление белого – событие С. Число всех исходов опыта равно числу шаров, т.е. n = 10, число благоприятствующих событиям исходов соответственно равно mA =3, mB = 2, mC = 10 – 5 = 5. Тогда, в соответствием с формулой классического определения вероятности, получаем:
Вообще говоря, классическое определение вероятности – довольно относительное. Это обусловлено тем, что на практике сложно представить результат опыта в виде совокупности элементарных событий, доказать, что события равновероятные. Например, при проведении опыта с подбрасыванием монеты на результат опыта могут влиять такие факторы как несимметричность монеты, влияние ее формы на аэродинамические характеристики полета, атмосферные условия и т.д. В этой связи вводится понятие статистической вероятности события. Определение. Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов. W(A) = W(A) – относительная частота события А; m – число опыта, в которых событие Апроизошло; n – общее число проведенных опытов. Отличие относительной частоты от вероятности заключается в том, что вероятность вычисляется без непосредственного произведения опытов, а относительная частота – после опыта. Если при 12 выстрелах по мишени попадание отмечалось в 8 выстрелах, тогда, относительная частота попадания равна W(A) =
При достаточно большом числе произведенных опытов относительная частота изменяется мало, колеблясь около одного числа p. Это число может быть принято за статистическую вероятность события.
Чтобы преодолеть недостаток классического определения вероятности, связанный с бесконечностью числа элементарных исходов опыта, вводится понятие геометрической вероятности, т.е. вероятности попадания точки в какой – либо отрезок или часть плоскости (пространства). Введем понятие мера множества S: (обозначим Ω(S)) · Для множества точек начисловой прямой мерой является длина соответствующего числового промежутка; · Мерой множества точек на плоскости является площадь фигуры, содержащей все эти точки; · Мерой множества точек трехмерного пространства является объем соответствующего тела. Так, если на отрезке AB длиной Ω(AB) = L выделен отрезок A1B1 длины Ω(A1B1) = l, то вероятность попадания наугад взятой точки в отрезок A1B1 равна отношению l/L. Пример: Найти вероятность тог, что случайно брошенная в квадрат со стороной 4 единицы точка попадет в заштрихованную область (см. рисунок).
Решение: Площадь всего квадрата Ω(S) = 4·4 = 16; площадь отмеченной части Ω(s) = 9. Искомая вероятность: P = 9/16 = 0,5625. §3. Операции над событиями.
Определение. События А и Вназываются равными, если осуществление события А влечет за собой осуществление события Ви наоборот.
Определение. Объединениемили суммой событий A1,A2,…,Аk называется событие A, которое заключается в появление хотя бы одногоиз событий Аk.
Определение. Пересечениемили произведениемсобытийA1,A2,…, Akназывается событие А, которое заключается в осуществлении всех событий Ak.
Замечание: Если в словесной форме между событиями произносится союз «и», то имеет место произведение событий, а если произносится союз «или», то имеет место сумма событий.
Примеры: 1. В урне находятся 5 красных, 8 зеленых, 4 желтых и 3 черных шара. Наудачу извлекают один шар. Рассмотрим события: А – извлечен цветной (не черный) шар. Очевидно, что событие А наступит, если будет извлечен красныйили зеленый или желтыйшар, т.е. имеет место сумма событий А = К + З + Ж. 2. Три стрелка делают по одному выстрелу по мишени. Рассмотрим событие В: попадут только первый и третий стрелки. Введем обозначения событий: А1 – первый стрелок попал в мишень, тогда Ā1 – первый стрелок не попал в мишень (промахнулся), А2 – второй стрелок попал в мишень, Ā2 – второй стрелок промахнулся, А3 – третий стрелок попал в мишень, Ā3 – третий стрелок промахнулся. Событие В произойдет, если первый стрелок попадет в мишень и второй стрелок промахнется и третий стрелок попадет,т.е. будет иметь место произведение событий: В = А1· Ā2· А3.
§4. Теоремы о вероятности суммы событий.
Теорема (сложения вероятностей). Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Следствие 1: Если события
Следствие 2: Сумма вероятностей противоположных событий равна единице.
Теорема. Вероятность появления хотя бы одного из двух совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления.
Примеры: 1) На тарелке лежат одинаковые на вид пирожки с разной начинкой: три с мясом, три с яйцом, два с яблоком и два с изюмом. Какова вероятность того, что случайно выбранный пирожок окажется со сладкой начинкой (с яблоком или с изюмом)? Решение: Рассмотрим события : А – извлечен пирожок с яблоком; В – извлечен пирожок с изюмом. Число всех исходов испытания ( выбор одного пирожка) равно числу пирожков, т.е. n = 3 + 3 + 2 + 2 = 10; число благоприятных исходов: mA =2, mB = 2. События А и В несовместные; сумма А + В и есть событие, состоящее в выборе сладкого пирожка. По теореме о вероятности сумма двух несовместных событий получим: P(A + B) = P(A) + P(B) = 2/10 + 2/10 = 4/10 = 0,4. 2) Из колоды в 36 карт наудачу извлекают одну карту. Найти вероятность того, что это будет карта бубновой масти или туз. Решение: Рассмотрим события : А – извлечена карта бубновой масти; В – извлечен туз. Вероятности этих событий легко найти по классическому определению, т.к. mA =9 (в колоде 9 карт бубновой масти), mB = 4 ( в колоде 4 туза), n = 36 (число всех карт в колоде). Тогда P(A) = 9/39, P(B) = 4/36. События А и В совместные (т.к. если будет извлечен бубновый туз, то произойдут оба события). Совместное появление этих событий имеет один благоприятный исход – появление бубнового туза, т.е.P(AB) = 1/36. Очевидно, что сумма А + В и есть событие, состоящее в появлении карты бубновой масти или туза. По теореме появления хотя бы одного из двух совместных событий имеем P(A+B) = P(A) + P(B) – P(AB) = 9/36 + 4/36 – 1/36 = 12/36 = 1/3.
|
,
.
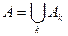= A1+A2+…+Ak
= A1·A2·…·Ak
образуют полную группу несовместных событий, то сумма их вероятностей равна единице.
