 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Рядов с положительными членами 12
Числовые и функциональные ряды Понятие числового ряда. Ряды с положительными членами
П.2.1.1 Основные понятия
Опр.Даны члены числовой последовательности (действительные или комплексные числа) u1, u2, …, un, … . Выражение u1+u2+…+un+… называется числовым рядом. Числа u1, u2, …, un, … называются членами ряда. un – общий член ряда. Сокращенно ряд записывают Запишем суммы S1 = u1, S2 = u1+u2, S3 = u1+u2+u3, … Sn = u1+u2+…+un, … их называют частными или частичными суммами ряда. Частные суммы образуют бесконечную числовую последовательность S1, S2, S3, …, Sn, … . Опр. Если существует конечный предел последовательности частных сумм Опр.Число S называют суммой ряда и записывают Опр. Если предел последовательности частных сумм не существует или равен бесконечности, то ряд называется расходящимся.
Пример Задан ряд: Запишем частную сумму ряда:
Члены ряда представим следующим образом:
Ряд сходится, и его сумма равна 1.
Опр. Ряд u1 + u2 + … + un + … называется рядом с положительными членами, если при всех значениях n выполняется неравенство un > 0.
Опр.Пусть даны два ряда с положительными членами
Если при всех значениях n выполняется неравенство
П.2.1.2. Простейшие свойства рядов. Необходимый признак сходимости
Теорема 1. Если у сходящегося ряда отбросить конечное число его членов, то полученный ряд также будет сходиться. Верно и обратное, если сходится ряд, полученный отбрасыванием конечного числа членов у данного ряда, то и данный ряд также сходится.
Т.о., сходимость ряда не меняется при отбрасывании любого конечного числа его членов. Теорема 2. Пусть ряд Теорема 3. Пусть ряды Необходимый признак сходимости:Если ряд Т.о., если Пример: Проверить, выполняется ли НПС для ряда Рассмотрим известные ряды: 1. Ряд, составленный из членов бесконечной геометрической прогрессии Если 2. Гармонический ряд 3. Ряд Дирихле 4. Эквивалентности при П.2.1.3. Достаточные признаки сходимости рядов с положительными членами
Признаки сравнения: 1-й признак Даны знакоположительные ряды 1) если 2) если Доказательство: Пусть 1) Пусть ряд (2) сходится, т.е. существует предел последовательности:
Т.о., последовательность частичных сумм ряда (1) монотонно возрастает и ограничена сверху числом По теореме существования предела, эта последовательность имеет конечный предел, т.е. ряд сходится. 2) Пусть ряд (1) расходится, т.е.
Замечание к 1 признаку сравнения: Трудность применения признака заключается в том, что для данного ряда нужно подобрать ряд (эталон). В качестве эталона расходящегося ряда чаще всего берут гармонический ряд.
Пример: 1. Исследовать на сходимость ряд: Сравним данный ряд с гармоническим рядом: По признаку сравнения из расходимости гармонического ряда, следует расходимость исходного ряда. 2. Исследовать сходимость ряда: Члены данного ряда не больше соответствующих членов ряда Ряд
2-ой признак Даны знакоположительные ряды Без доказательства.
12 |




 .
. , то ряд называют сходящимся.
, то ряд называют сходящимся. .
.



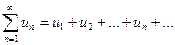 ,
,  .
. , то ряд
, то ряд  называется мажорантным (т.е. рядом с большими членами) по отношению к ряду
называется мажорантным (т.е. рядом с большими членами) по отношению к ряду 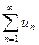 , а ряд
, а ряд  , где
, где  - произвольное число, также сходится, причем его сумма равна
- произвольное число, также сходится, причем его сумма равна  .
. и
и  . Тогда ряд
. Тогда ряд  также сходится, причем его сумма равна
также сходится, причем его сумма равна  .
. стремится к нулю при
стремится к нулю при  , т.е.
, т.е.  .
. , то ряд расходится.
, то ряд расходится. .
. , называется геометрическим рядом.
, называется геометрическим рядом. , то ряд расходится. Если
, то ряд расходится. Если  , то ряд сходится.
, то ряд сходится.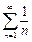 расходится.
расходится. ,
,  . Если
. Если  , то ряд сходится. Если
, то ряд сходится. Если  , то ряд расходится.
, то ряд расходится. :
: 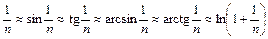
 (1) и
(1) и  (2), где
(2), где  . Тогда:
. Тогда: и
и  .
. . Тогда
. Тогда .
. , тогда
, тогда  , т.е. ряд (2) расходится.
, т.е. ряд (2) расходится. .
. .
. .
. , т. к.
, т. к.  .
. <1. Такой ряд сходится, следовательно, ряд
<1. Такой ряд сходится, следовательно, ряд  . Тогда ряды
. Тогда ряды