ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Лабораторная работа №7. Множественная регрессия. Способы определения параметров множественной регрессии 12
Множественный регрессионный анализ Задание 1. Определить аналитическое выражение связи между результативным признаком Y и факторными признаками х1, х2, х3, х4; на основе данных таблицы 1 построить уравнение множественной регрессии:
Методом Крамера (метод определителей) рассчитать параметры регрессии.
Таблица 1 – Исходные данные для расчета параметров множественной регрессии
Решение: 1. Построить таблицу 2.
2.Система нормальных уравнений
Построить матрицу Х из коэффициентов при неизвестных а0, а1, а2, а3, а4 и столбец-вектор В из правой части системы уравнений:
Заполнить матрицу Х:
3.Скопировать матрицу Х5 раз и заменить соответствующие столбцы Х столбцом В:
4. Вычислить общий определитель матрицы (∆) и преобразованных матриц (∆а0, ∆а1, ∆а2, ∆а3, ∆а4) встроенной функцией МОПРЕД() и вычислить а0, а1, а2, а3, а4:
5. Ввести в таблицу столбецỹ и сделать расчеты. Если суммы y и ỹ совпадают, то параметры уравнения линейной регрессии аiопределены статистически верно.
6.Найти среднюю ошибку аппроксимации.
7. Выполните регрессионный анализ с помощью функции Регрессия (Анализ данных). Задание 2. Используя метод информационной емкости подобрать факторы, объясняющие результирующие переменные. Таблица 3 – Исходные данные зависимой переменной и факторов
Решение: Выбрать объясняющие переменные при помощи метода показателей информационной емкости.
Построить матрицу межфакторной корреляции (Анализ_данных – Корреляция):
– вектор коэффициентов корреляции:
– матрица коэффициентов межфакторной корреляции:
Т.к. рассматриваются 4 потенциальные объясняющие переменные, необходимо проанализировать С1=X1; C5=(X1,X2); C11=(X1,X2,X3); C2=X2; C6=(X1,X3); C12=(X1,X2,X4); C3=X3; C7=(X1,X4); C13=(X1,X3,X4); C4=X4; C8=(X2,X3); C14=(X2,X3,X4); C9=(X2,X4); C15=(X1,X2,X3,X4). C10=(X3,X4); Для одноэлементных комбинаций индивидуальный показатель емкости (вес): H1=h11=r12= (0,08)2=0,006; H2=h22=r22= (0,02)2=0,0004; H3=h33=r32= (-0,21)2=0,043; H4=h44=r42= (-0,2)2=0,041.
Для 2-х элементной комбинации C5=(X1,X2) рассчитываются 2 индивидуальных показателя информационной емкости: h51 для Х1и h52 для Х2:
Интегральный показатель веса: H5=h51+h52=0,0039.
Для остальных 2-х элементных комбинаций: h61=0,0056; h63=0,0402; H6=0,046; h71=0,0056; h74=0,0385; H7=0,044; h82=0,0003; h83=0,0355; H8=0,035; h92=0,0003; h94=0,0340; H9=0,034; h10,3=0,022; h10,4=0,021; H10=0,04.
Для 3-х элементной комбинации C11=(X1,X2,X3) индивидуальные показатели информационной емкости:
Интегральный показатель веса: H11=h11,1+h11,2+h11,3=0,0376.
Для остальных 3-х элементных комбинаций:
Индивидуальные показатели веса переменных X1, X2, X3 и X4 (комбинация С15):
H15=h15,1+h15,2+h15,3+h15,4=0,0416. Максимальное значение интегрального показателя веса равно 0,0471 и относится к комбинации С13, включающей переменную X1, Х3,иХ4.
В результате модель примет вид:
Лабораторная работа №8. Определение параметров множественной регрессии в стандартизованной и естественной формах
Задание 1. Для данных, представленных в таблице 3 построить уравнение множественной регрессии в стандартизованной и естественной форме.
Таблица 3 – Расчетные данные для построения уравнения регрессии
Требуется: 1.Построить уравнение множественной регрессии в стандартизованной и естественной форме 2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними; 3. Рассчитать частные коэффициенты эластичности, сравнить их с b1 и b2, пояснить различия между ними. 4. Рассчитать общий и частные F-критерии Фишера. Решение: Для уравнения множественной регрессии в стандартизованном масштабе ty=b1*tx1+b1*tx2рассчитать коэффициенты bi:
В результате ty=0,8273*tx1–0,1141*tx2
Линейное уравнение множественной регрессии в естественной форме: y=a+b1x1+b2x2
Для b1 b2,… , а:
Рассчитать коэффициенты эластичности:
В результате
Рассчитать коэффициент множественной корреляции:
Общий F-критерий проверяет гипотезу Но о статистической значимости уравнения регрессии и показателя тесноты связи (R2 = О):
Fтабл=<Fфакт
Частные F-критерии – Fх1факт и Fх2факт оценивают статистическую значимость присутствия факторов x1 и х2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора. Целесообразность включения в модель фактора х1 после фактора x2 проверяет Fх1:
Fх2факт<Fтабл свидетельствует о статистической незначимости прироста R2y за счет включения в модель фактора х2 после фактора x1.
Задание 2. Составить уравнение множественной регрессии Оценить качество модели.
Параметры множественной регрессии определить с помощью уравнения регрессии в стандартизированном масштабе:
Коэффициенты β1, β2, ... βр:
где Dbi - частные определители; D - общий определитель.
Найти параметры b1 b2,…,bp:
Таблица 4 – Исходные данные для расчета параметров множественной регрессии
Решение: 1. Построить матрицу парных коэффициентов корреляции (Анализ данных-Корреляция):
Матрица межфакторной корреляции:
Заполнить матрицу межфакторной корреляции:
2.Вычислить общий определитель (∆) матрицы межфакторной корреляции: ∆=0,00158
3. Скопировать матрицу межфакторной корреляции 5 раз. Соответствующий i-ый столбец матрицы заменяется столбцом корреляции между у и хi. Вычислить частные определители Dbi и значения параметров уравнения множественной регрессии b1, b2, b3, b4, b5, a:
В итоге уравнение множественной регрессии:
4.Оценить качество модели через среднюю ошибку аппроксимации.
5. Выполните регрессионный анализ функцией Регрессия (Анализ данных) 12 |





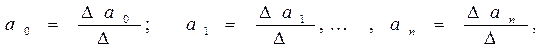






 комбинаций переменных:
комбинаций переменных: ;
;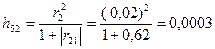 .
. ;
; ;
;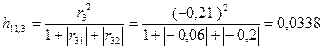 .
.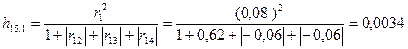 ;
; ;
; ;
; ;
;
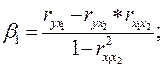
 .
.






 Fтабл=3,4; a=0,05
Fтабл=3,4; a=0,05 Fгабл =4,21; a =0,05
Fгабл =4,21; a =0,05









 = -0,0005;
= -0,0005;