 ПОЗНАВАТЕЛЬНОЕ Сила воли ведет к действию, а позитивные действия формируют позитивное отношение Как определить диапазон голоса - ваш вокал Игровые автоматы с быстрым выводом Как самому избавиться от обидчивости Противоречивые взгляды на качества, присущие мужчинам Вкуснейший "Салат из свеклы с чесноком" Натюрморт и его изобразительные возможности Применение, как принимать мумие? Мумие для волос, лица, при переломах, при кровотечении и т.д. Как научиться брать на себя ответственность Зачем нужны границы в отношениях с детьми? Световозвращающие элементы на детской одежде Как победить свой возраст? Восемь уникальных способов, которые помогут достичь долголетия Классификация ожирения по ИМТ (ВОЗ) Глава 3. Завет мужчины с женщиной Оси и плоскости тела человека - Тело человека состоит из определенных топографических частей и участков, в которых расположены органы, мышцы, сосуды, нервы и т.д.
| Решение системы дифференциальных уравнений. 12
Существует огромное количество методов решения системы нелинейных дифференциальных уравнений: метод Эйлера, экстраполяционные методы Адамса, метод Милна и т.д. Также одним из распространенных методов решения системы дифференциальных уравнений является метод Рунге-Кутты, который рассмотрим в качестве примера более подробно. Методы Рунге-Кутты— важное семейство численных алгоритмов решения обыкновенных дифференциальных уравнений и их систем. Формально, методом Рунге — Кутты является модифицированный и исправленный метод Эйлера, они представляют собой схемы второго порядка точности. Существуют стандартные схемы третьего порядка, не получившие широкого распространения. Наиболее часто используется и реализована в различных математических пакетах (Maple, MathCAD, Maxima) стандартная схема четвёртого порядка. Иногда при выполнении расчётов с повышенной точностью применяются схемы пятого и шестого порядков. Построение схем более высокого порядка сопряжено с большими вычислительными трудностями. Классический метод Рунге — Кутты 4 порядка Метод Рунге — Кутты 4 порядка столь широко распространён, что его часто называют просто методом Рунге — Кутты. Рассмотрим задачу Коши
Тогда приближенное значение в последующих точках вычисляется по итерационной формуле:
Вычисление нового значения проходит в четыре стадии:
где Этот метод имеет четвёртый порядок точности, то есть суммарная ошибка на конечном интервале интегрирования имеет порядок
Практическая часть Программный модуль:
Программный модуль включает две управляющие кнопки: - Решить - решает систему дифференциальных уравнений и выводит решение в виде графика временной реализации, x(t). - Очистить - очищает поле для построения графиков.
Возможно интерактивное изменение диапазона времени, которое выводится на графике. M - количество шагов, до вывода точек на график, N - количество шагов, которые выводим на график. Возможно интерактивное изменение управляющих параметров m и g.
Текст программы, написанный на языке программирования Delphi. unit AA;
interface
uses Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, TeEngine, Series, ExtCtrls, TeeProcs, Chart,Math, Buttons;
type TForm1 = class(TForm) Button1: TButton; Button2: TButton; GroupBox2: TGroupBox; Edit4: TEdit; Edit5: TEdit; Label4: TLabel; Label5: TLabel; Label2: TLabel; Label3: TLabel; Edit2: TEdit; Label7: TLabel; Edit3: TEdit; Chart1: TChart; Series1: TLineSeries; procedure Button2Click(Sender: TObject); procedure Button1Click(Sender: TObject); private { Private declarations } public { Public declarations } end;
//Const //h=0.03; var Form1: TForm1; i,N,M:integer; mm,gg:extended; xr,yr,zr,tt,xn,yn,zn,tn,dx,dy,dz,h:real; implementation
{$R *.dfm} function ll(x:real):real; begin if x<=0 then result:=0; if x>0 then result:=1; end;
function f1(t,x,y,z:real):real; begin result:=mm*x+y-x*z; end; function f2(t,x,y,z:real):real; begin result:=-x; end; function f3(t,x,y,z:real):real; begin result:=-gg*z+ll(x)*x*x; end;
procedure RG(var tt,x,y,z:real); var k11,k12,k13,k14,k21,k22,k23,k24,k31,k32,k33,k34:real; begin k11:=h*f1(tt,x,y,z); k21:=h*f2(tt,x,y,z); k31:=h*f3(tt,x,y,z); k12:=h*f1(tt+h/2,x+k11/2,y+k21/2,z+k31/2); k22:=h*f2(tt+h/2,x+k11/2,y+k21/2,z+k31/2); k32:=h*f3(tt+h/2,x+k11/2,y+k21/2,z+k31/2); k13:=h*f1(tt+h/2,x+k12/2,y+k22/2,z+k32/2); k23:=h*f2(tt+h/2,x+k12/2,y+k22/2,z+k32/2); k33:=h*f3(tt+h/2,x+k12/2,y+k22/2,z+k32/2); k14:=h*f1(tt+h,x+k13,y+k23,z+k33{/2}); k24:=h*f2(tt+h,x+k13,y+k23,z+k33{/2}); k34:=h*f3(tt+h,x+k13,y+k23,z+k33{/2}); dx:=(k11+2*k12+2*k13+k14)/6; dy:=(k21+2*k22+2*k23+k24)/6; dz:=(k31+2*k32+2*k33+k34)/6; end;
procedure TForm1.Button2Click(Sender: TObject); begin Series1.Clear; end;
procedure TForm1.Button1Click(Sender: TObject); begin DecimalSeparator:='.'; Series1.Clear; h:=0.01; M:=StrToInt(Edit2.Text); N:=StrToInt(Edit3.Text); mm:=StrToFloat(Edit4.Text); gg:=StrToFloat(Edit5.Text); tt:=0; xr:=0.5; yr:=0.5; zr:=0.5; i:=0; While i<=M do Begin RG(tt,xr,yr,zr); xn:=xr+dx; yn:=yr+dy; zn:=zr+dz; tn:=tt+h; if xn*xr<=0 then i:=i+1; xr:=xn; yr:=yn; zr:=zn; tt:=tn; end; i:=0; While i<=N do begin RG(tt,xr,yr,zr); xn:=xr+dx; yn:=yr+dy; zn:=zr+dz; tn:=tt+h; Series1.AddXY(tt,xr); if xn*xr<=0 then i:=i+1; xr:=xn; yr:=yn; zr:=zn; tt:=tn; end; end;
end. 12 |






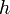 — величина шага по времени t.
— величина шага по времени t. .
.